Angle between crossing lines (2019). Angles with aligned sides. Angle between straight lines The concept of an angle between parallel intersecting lines
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.
It will be useful for every student who is preparing for the Unified State Exam in mathematics to repeat the topic “Finding an angle between straight lines.” As statistics show, when passing the certification test, tasks in this section of stereometry cause difficulties for a large number of students. At the same time, tasks that require finding the angle between straight lines are found in the Unified State Exam at both the basic and specialized levels. This means that everyone should be able to solve them.
Basic moments
There are 4 types of relative positions of lines in space. They can coincide, intersect, be parallel or intersecting. The angle between them can be acute or straight.
To find the angle between lines in the Unified State Exam or, for example, in solving, schoolchildren in Moscow and other cities can use several ways to solve problems in this section of stereometry. You can complete the task using classical constructions. To do this, it is worth learning the basic axioms and theorems of stereometry. The student needs to be able to reason logically and create drawings in order to bring the task to a planimetric problem.
You can also use the coordinate vector method using simple formulas, rules and algorithms. The main thing in this case is to perform all calculations correctly. The Shkolkovo educational project will help you hone your problem-solving skills in stereometry and other sections of the school course.
Oh-oh-oh-oh-oh... well, it’s tough, as if he was reading out a sentence to himself =) However, relaxation will help later, especially since today I bought the appropriate accessories. Therefore, let's proceed to the first section, I hope that by the end of the article I will maintain a cheerful mood.
The relative position of two lines
This is the case when the audience sings along in chorus. Two straight lines can:
1) match;
2) be parallel: ;
3) or intersect at a single point: .
Help for dummies : Please remember the mathematical intersection sign, it will appear very often. The notation means that the line intersects with the line at point .
How to determine the relative position of two lines?
Let's start with the first case:
Two lines coincide if and only if their corresponding coefficients are proportional, that is, there is a number “lambda” such that the equalities are satisfied
Let's consider the straight lines and create three equations from the corresponding coefficients: . From each equation it follows that, therefore, these lines coincide.
Indeed, if all the coefficients of the equation ![]() multiply by –1 (change signs), and all coefficients of the equation
multiply by –1 (change signs), and all coefficients of the equation ![]() cut by 2, you get the same equation: .
cut by 2, you get the same equation: .
The second case, when the lines are parallel:
Two lines are parallel if and only if their coefficients of the variables are proportional: ![]() , But.
, But.
As an example, consider two straight lines. We check the proportionality of the corresponding coefficients for the variables: ![]()
However, it is quite obvious that.
And the third case, when the lines intersect:
Two lines intersect if and only if their coefficients of the variables are NOT proportional, that is, there is NO such value of “lambda” that the equalities are satisfied ![]()
So, for straight lines we will create a system: ![]()
From the first equation it follows that , and from the second equation: , which means the system is inconsistent(no solutions). Thus, the coefficients of the variables are not proportional.
Conclusion: lines intersect
In practical problems, you can use the solution scheme just discussed. By the way, it is very reminiscent of the algorithm for checking vectors for collinearity, which we looked at in class The concept of linear (in)dependence of vectors. Basis of vectors. But there is a more civilized packaging:
Example 1
Find out the relative position of the lines: 
Solution based on the study of directing vectors of straight lines:
a) From the equations we find the direction vectors of the lines: ![]() .
.
, which means that the vectors are not collinear and the lines intersect.
Just in case, I’ll put a stone with signs at the crossroads:
The rest jump over the stone and follow further, straight to Kashchei the Immortal =)
b) Find the direction vectors of the lines: ![]()
The lines have the same direction vector, which means they are either parallel or coincident. There is no need to count the determinant here.
It is obvious that the coefficients of the unknowns are proportional, and .
Let's find out whether the equality is true: ![]()
Thus,
c) Find the direction vectors of the lines: ![]()
Let's calculate the determinant made up of the coordinates of these vectors: ![]() , therefore, the direction vectors are collinear. The lines are either parallel or coincident.
, therefore, the direction vectors are collinear. The lines are either parallel or coincident.
The proportionality coefficient “lambda” is easy to see directly from the ratio of collinear direction vectors. However, it can also be found through the coefficients of the equations themselves: ![]() .
.
Now let's find out whether the equality is true. Both free terms are zero, so:
The resulting value satisfies this equation (any number in general satisfies it).
Thus, the lines coincide.
Answer:
Very soon you will learn (or even have already learned) to solve the problem discussed verbally literally in a matter of seconds. In this regard, I don’t see any point in offering anything for an independent solution; it’s better to lay another important brick in the geometric foundation:
How to construct a line parallel to a given one?
For ignorance of this simplest task, the Nightingale the Robber severely punishes.
Example 2
The straight line is given by the equation. Write an equation for a parallel line that passes through the point.
Solution: Let's denote the unknown line by the letter . What does the condition say about her? The straight line passes through the point. And if the lines are parallel, then it is obvious that the direction vector of the straight line “tse” is also suitable for constructing the straight line “de”.
We take the direction vector out of the equation:
Answer:
The geometry of the example looks simple: 
Analytical testing consists of the following steps:
1) We check that the lines have the same direction vector (if the equation of the line is not simplified properly, then the vectors will be collinear).
2) Check whether the point satisfies the resulting equation.
In most cases, analytical testing can be easily performed orally. Look at the two equations, and many of you will quickly determine the parallelism of the lines without any drawing.
Examples for independent solutions today will be creative. Because you will still have to compete with Baba Yaga, and she, you know, is a lover of all sorts of riddles.
Example 3
Write an equation for a line passing through a point parallel to the line if
There is a rational and not so rational way to solve it. The shortest way is at the end of the lesson.
We worked a little with parallel lines and will return to them later. The case of coinciding lines is of little interest, so let’s consider a problem that is very familiar to you from the school curriculum:
How to find the point of intersection of two lines?
If straight ![]() intersect at point , then its coordinates are the solution systems of linear equations
intersect at point , then its coordinates are the solution systems of linear equations ![]()
How to find the point of intersection of lines? Solve the system.
Here you go geometric meaning of a system of two linear equations with two unknowns- these are two intersecting (most often) lines on a plane.
Example 4
Find the point of intersection of lines
Solution: There are two ways to solve - graphical and analytical.
The graphical method is to simply draw the given lines and find out the intersection point directly from the drawing: 
Here is our point: . To check, you should substitute its coordinates into each equation of the line, they should fit both there and there. In other words, the coordinates of a point are a solution to the system. Essentially, we looked at a graphical solution systems of linear equations with two equations, two unknowns.
The graphical method is, of course, not bad, but there are noticeable disadvantages. No, the point is not that seventh graders decide this way, the point is that it will take time to create a correct and ACCURATE drawing. In addition, some straight lines are not so easy to construct, and the point of intersection itself may be located somewhere in the thirtieth kingdom outside the notebook sheet.
Therefore, it is more expedient to search for the intersection point using an analytical method. Let's solve the system: 
To solve the system, the method of term-by-term addition of equations was used. To develop relevant skills, take a lesson How to solve a system of equations?
Answer:
The check is trivial - the coordinates of the intersection point must satisfy each equation of the system.
Example 5
Find the point of intersection of the lines if they intersect.
This is an example for you to solve on your own. It is convenient to split the task into several stages. Analysis of the condition suggests that it is necessary:
1) Write down the equation of the straight line.
2) Write down the equation of the straight line.
3) Find out the relative position of the lines.
4) If the lines intersect, then find the point of intersection.
The development of an action algorithm is typical for many geometric problems, and I will repeatedly focus on this.
Full solution and answer at the end of the lesson:
Not even a pair of shoes were worn out before we got to the second section of the lesson:
Perpendicular lines. Distance from a point to a line.
Angle between straight lines
Let's start with a typical and very important task. In the first part, we learned how to build a straight line parallel to this one, and now the hut on chicken legs will turn 90 degrees:
How to construct a line perpendicular to a given one?
Example 6
The straight line is given by the equation. Write an equation perpendicular to the line passing through the point.
Solution: By condition it is known that . It would be nice to find the directing vector of the line. Since the lines are perpendicular, the trick is simple:
From the equation we “remove” the normal vector: , which will be the directing vector of the straight line.
Let's compose the equation of a straight line using a point and a direction vector:
Answer: ![]()
Let's expand the geometric sketch:

Hmmm... Orange sky, orange sea, orange camel.
Analytical verification of the solution:
1) We take out the direction vectors from the equations and use scalar product of vectors we come to the conclusion that the lines are indeed perpendicular: .
By the way, you can use normal vectors, it's even easier.
2) Check whether the point satisfies the resulting equation ![]() .
.
The test, again, is easy to perform orally.
Example 7
Find the point of intersection of perpendicular lines if the equation is known ![]() and period.
and period.
This is an example for you to solve on your own. There are several actions in the problem, so it is convenient to formulate the solution point by point.
Our exciting journey continues:
Distance from point to line
In front of us is a straight strip of the river and our task is to get to it by the shortest route. There are no obstacles, and the most optimal route will be to move along the perpendicular. That is, the distance from a point to a line is the length of the perpendicular segment.
Distance in geometry is traditionally denoted by the Greek letter “rho”, for example: – the distance from the point “em” to the straight line “de”.
Distance from point to line ![]() expressed by the formula
expressed by the formula![]()
Example 8
Find the distance from a point to a line ![]()
Solution: all you need to do is carefully substitute the numbers into the formula and carry out the calculations:
Answer: ![]()
Let's make the drawing: 
The found distance from the point to the line is exactly the length of the red segment. If you draw up a drawing on checkered paper on a scale of 1 unit. = 1 cm (2 cells), then the distance can be measured with an ordinary ruler.
Let's consider another task based on the same drawing:
The task is to find the coordinates of a point that is symmetrical to the point relative to the straight line ![]() . I suggest performing the steps yourself, but I will outline a solution algorithm with intermediate results:
. I suggest performing the steps yourself, but I will outline a solution algorithm with intermediate results:
1) Find a line that is perpendicular to the line.
2) Find the point of intersection of the lines: ![]() .
.
Both actions are discussed in detail in this lesson.
3) The point is the midpoint of the segment. We know the coordinates of the middle and one of the ends. By formulas for the coordinates of the midpoint of a segment we find .
It would be a good idea to check that the distance is also 2.2 units.
Difficulties may arise in calculations here, but a microcalculator is a great help in the tower, allowing you to calculate ordinary fractions. I have advised you many times and will recommend you again.
How to find the distance between two parallel lines?
Example 9
Find the distance between two parallel lines
This is another example for you to decide on your own. I’ll give you a little hint: there are infinitely many ways to solve this. Debriefing at the end of the lesson, but it’s better to try to guess for yourself, I think your ingenuity was well developed.
Angle between two straight lines
Every corner is a jamb: 
In geometry, the angle between two straight lines is taken to be the SMALLER angle, from which it automatically follows that it cannot be obtuse. In the figure, the angle indicated by the red arc is not considered the angle between intersecting lines. And his “green” neighbor or oppositely oriented"raspberry" corner.
If the lines are perpendicular, then any of the 4 angles can be taken as the angle between them.
How are the angles different? Orientation. Firstly, the direction in which the angle is “scrolled” is fundamentally important. Secondly, a negatively oriented angle is written with a minus sign, for example if .
Why did I tell you this? It seems that we can get by with the usual concept of an angle. The fact is that the formulas by which we will find angles can easily result in a negative result, and this should not take you by surprise. An angle with a minus sign is no worse, and has a very specific geometric meaning. In the drawing, for a negative angle, be sure to indicate its orientation with an arrow (clockwise).
How to find the angle between two straight lines? There are two working formulas:
Example 10
Find the angle between lines
Solution And Method one
Let's consider two straight lines defined by equations in general form: ![]()
If straight not perpendicular, That oriented The angle between them can be calculated using the formula: 
Let us pay close attention to the denominator - this is exactly scalar product directing vectors of straight lines:
If , then the denominator of the formula becomes zero, and the vectors will be orthogonal and the lines will be perpendicular. That is why a reservation was made about the non-perpendicularity of straight lines in the formulation.
Based on the above, it is convenient to formalize the solution in two steps:
1) Let's calculate the scalar product of the direction vectors of the lines:
, which means the lines are not perpendicular.
2) Find the angle between straight lines using the formula:

Using the inverse function, it is easy to find the angle itself. In this case, we use the oddness of the arctangent (see. Graphs and properties of elementary functions):![]()
Answer: ![]()
In your answer, we indicate the exact value, as well as an approximate value (preferably in both degrees and radians), calculated using a calculator.
Well, minus, minus, no big deal. Here is a geometric illustration: 
It is not surprising that the angle turned out to be of a negative orientation, because in the problem statement the first number is a straight line and the “unscrewing” of the angle began precisely with it.
If you really want to get a positive angle, you need to swap the lines, that is, take the coefficients from the second equation ![]() , and take the coefficients from the first equation. In short, you need to start with a direct
, and take the coefficients from the first equation. In short, you need to start with a direct ![]() .
.
In this article, we will first define the angle between crossing lines and provide a graphic illustration. Next, we will answer the question: “How to find the angle between crossing lines if the coordinates of the direction vectors of these lines in a rectangular coordinate system are known”? In conclusion, we will practice finding the angle between intersecting lines when solving examples and problems.
Page navigation.
Angle between intersecting straight lines - definition.
We will approach determining the angle between intersecting straight lines gradually.
First, let us recall the definition of skew lines: two lines in three-dimensional space are called interbreeding, if they do not lie in the same plane. From this definition it follows that intersecting lines do not intersect, are not parallel, and, moreover, do not coincide, otherwise they would both lie in a certain plane.
Let us give further auxiliary reasoning.
Let two intersecting lines a and b be given in three-dimensional space. Let's construct straight lines a 1 and b 1 so that they are parallel to the skew lines a and b, respectively, and pass through some point in space M 1 . Thus, we get two intersecting lines a 1 and b 1. Let the angle between intersecting lines a 1 and b 1 be equal to angle . Now let's construct lines a 2 and b 2, parallel to the skew lines a and b, respectively, passing through a point M 2, different from the point M 1. The angle between the intersecting lines a 2 and b 2 will also be equal to the angle. This statement is true, since straight lines a 1 and b 1 will coincide with straight lines a 2 and b 2, respectively, if a parallel transfer is performed, in which point M 1 moves to point M 2. Thus, the measure of the angle between two straight lines intersecting at a point M, respectively parallel to the given intersecting lines, does not depend on the choice of point M.
Now we are ready to define the angle between intersecting lines.
Definition.
Angle between intersecting lines is the angle between two intersecting lines that are respectively parallel to the given intersecting lines.
From the definition it follows that the angle between crossing lines will also not depend on the choice of point M. Therefore, as a point M we can take any point belonging to one of the intersecting lines.
Let us give an illustration of determining the angle between intersecting lines.

Finding the angle between intersecting lines.
Since the angle between intersecting lines is determined through the angle between intersecting lines, finding the angle between intersecting lines is reduced to finding the angle between the corresponding intersecting lines in three-dimensional space.
Undoubtedly, the methods studied in geometry lessons in high school are suitable for finding the angle between skew lines. That is, having completed the necessary constructions, you can connect the desired angle with any angle known from the condition, based on the equality or similarity of the figures, in some cases it will help cosine theorem, and sometimes leads to the result definition of sine, cosine and tangent of an angle right triangle.
However, it is very convenient to solve the problem of finding the angle between crossing lines using the coordinate method. That's what we'll consider.
Let Oxyz be introduced in three-dimensional space (however, in many problems you have to enter it yourself).
Let us set ourselves a task: find the angle between the crossing lines a and b, which correspond to some equations of a line in space in the rectangular coordinate system Oxyz.
Let's solve it.
Let's take an arbitrary point in three-dimensional space M and assume that straight lines a 1 and b 1 pass through it, parallel to the crossing straight lines a and b, respectively. Then the required angle between the intersecting lines a and b is equal to the angle between the intersecting lines a 1 and b 1 by definition.
Thus, we just have to find the angle between intersecting lines a 1 and b 1. To apply the formula for finding the angle between two intersecting lines in space, we need to know the coordinates of the direction vectors of the lines a 1 and b 1.
How can we get them? And it's very simple. The definition of the direction vector of a straight line allows us to assert that the sets of direction vectors of parallel lines coincide. Therefore, the direction vectors of straight lines a 1 and b 1 can be taken as direction vectors ![]() And
And ![]() straight lines a and b respectively.
straight lines a and b respectively.
So, The angle between two intersecting lines a and b is calculated by the formula  , Where
, Where ![]() And
And ![]() are the direction vectors of straight lines a and b, respectively.
are the direction vectors of straight lines a and b, respectively.
Formula for finding the cosine of the angle between crossing lines a and b have the form  .
.
Allows you to find the sine of the angle between crossing lines if the cosine is known: ![]() .
.
It remains to analyze the solutions to the examples.
Example.
Find the angle between the crossing lines a and b, which are defined in the Oxyz rectangular coordinate system by the equations ![]() And
And  .
.
Solution.
The canonical equations of a straight line in space allow you to immediately determine the coordinates of the directing vector of this straight line - they are given by the numbers in the denominators of the fractions, that is, ![]()
![]() . Parametric equations of a straight line in space also make it possible to immediately write down the coordinates of the direction vector - they are equal to the coefficients in front of the parameter, that is,
. Parametric equations of a straight line in space also make it possible to immediately write down the coordinates of the direction vector - they are equal to the coefficients in front of the parameter, that is, ![]() - direct vector
- direct vector  . Thus, we have all the necessary data to apply the formula by which the angle between intersecting lines is calculated:
. Thus, we have all the necessary data to apply the formula by which the angle between intersecting lines is calculated: 
Answer:
The angle between the given intersecting lines is equal to .
Example.
Find the sine and cosine of the angle between the crossing lines on which the edges AD and BC of the pyramid ABCD lie, if the coordinates of its vertices are known: .
Solution.
The direction vectors of the crossing lines AD and BC are the vectors and . Let's calculate their coordinates as the difference between the corresponding coordinates of the end and beginning points of the vector: 
According to the formula  we can calculate the cosine of the angle between the specified crossing lines:
we can calculate the cosine of the angle between the specified crossing lines:
Now let's calculate the sine of the angle between the crossing lines: 
Parallel lines. Distance between parallel lines.
.
Corresponding angles
.
Internal and external crosswise angles
.
Internal and external one-sided corners .
Angles with correspondingly perpendicular sides
.
Proportional segments
. Thales's theorem.
Two straight lines AB and CD (Fig. 11) are called parallel, if they lie in the same plane and do not intersect, no matter how long they continue. Designation: AB || CD . All points of one parallel line are at the same distance from another parallel line. All lines parallel to one line are parallel to each other. It is generally accepted that the angle between parallel lines is zero. Angle between two parallel rays is equal to zero if they have the same directions, and 180° , if their directions are opposite. All perpendiculars ( AB, CD, EF , Fig. 12) to the same straight line K.M. parallelbetween themselves. Reverse, direct K.M. , perpendicular to one of parallel lines, is perpendicular to the others. Length perpendicular segment between two parallel lines, There is distance between them.
When two parallel lines intersect with a third straight line, eight angles are formed (Fig. 13), which are called in pairs:
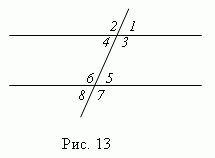
1) corresponding angles (1 And 5; 2 And 6; 3 And 7; 4 And 8 ); these angles are in pairs
are equal: ( 1 = 5; 2 = 6; 3 = 7; 4 = 8 );
2) internal crosswise angles (4 And 5; 3 And 6 ); they are pairwise equal;
3) external crosswise angles (1 And 8; 2 And 7 ); they are pairwise equal;
4) internal one-sided corners (3 And 5; 4 And 6 ); their sum is 180°
( 3 + 5 = 180
° ; 4 + 6 = 180 ° );5) external one-sided corners (1 And 7; 2 And 8 ); their sum is 180°
( 1 + 7 = 180° ; 2 + 8 = 180 ° ).
Angles with correspondingly parallel sides or equal to each other ( if they are both sharp or both dull, 1 = 2 , Fig. 14), or their sum is 180° ( 3 + 4 = 180°, Fig. 15).






