किन समतलों को समांतर कहते हैं, उदाहरण दीजिए। विमानों की समानता: संकेत, स्थिति। उदाहरण के द्वारा समानांतर विमान

अंतरिक्ष में विमान की स्थिति निम्न द्वारा निर्धारित की जाती है:

• तीन बिंदु जो एक सीधी रेखा पर स्थित नहीं हैं;
• एक सीधी रेखा और सीधी रेखा के बाहर एक बिंदु;
• दो अन्तर्विभाजक रेखाएँ;
• दो समानांतर रेखाएँ;
• सपाट आंकड़ा।

इसके अनुसार, विमान को आरेख पर सेट किया जा सकता है:

• तीन बिंदुओं के प्रक्षेपण जो एक सीधी रेखा पर स्थित नहीं हैं (चित्र 3.1, ए);
• एक बिंदु और एक सीधी रेखा के अनुमान (चित्र 3.1, बी);
• दो अन्तर्विभाजक रेखाओं के अनुमान (चित्र 3.1, सी);
• दो समानांतर रेखाओं के अनुमान (चित्र 3.1, डी);
• एक सपाट आकृति (चित्र 3.1, ई);
• विमान के निशान;
• विमान की सबसे बड़ी ढलान की रेखा।

चित्रा 3.1 - विमानों को निर्दिष्ट करने के तरीके

सामान्य स्थिति में विमानएक ऐसा तल है जो किसी प्रक्षेपण तल के न तो समांतर है और न ही लंबवत है।

विमान का पीछा करते हुएप्रक्षेपण विमानों में से एक के साथ दिए गए विमान के चौराहे के परिणामस्वरूप प्राप्त एक सीधी रेखा कहा जाता है।

एक सामान्य विमान में तीन निशान हो सकते हैं: क्षैतिज – απ 1 , ललाट – απ 2 और प्रोफ़ाइल – απ 3 , जो ज्ञात प्रक्षेपण विमानों के साथ पार करते समय बनता है: क्षैतिज π 1 , ललाट π 2 और प्रोफ़ाइल π 3 (चित्र 3.2)।

चित्र 3.2 - सामान्य स्थिति के एक विमान के निशान

3.2। निजी स्थिति विमान

निजी स्थिति विमान- एक विमान लंबवत या अनुमानों के विमान के समानांतर।

प्रोजेक्शन प्लेन के लंबवत एक प्लेन को प्रोजेक्शन प्लेन कहा जाता है, और इसे इस प्रोजेक्शन प्लेन पर एक सीधी रेखा के रूप में प्रक्षेपित किया जाएगा।

प्रोजेक्शन विमान संपत्ति: प्रोजेक्टिंग प्लेन से संबंधित सभी बिंदुओं, रेखाओं, सपाट आकृतियों में प्लेन के झुके हुए निशान पर अनुमान होते हैं(चित्र 3.3)।

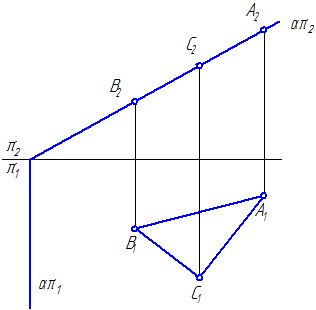
चित्रा 3.3 - फ्रंट-प्रोजेक्टिंग प्लेन जिससे वे संबंधित हैं: अंक ए, में, साथ; पंक्तियां एसी, अब, रवि; त्रिभुज विमान एबीसी

ललाट प्रक्षेपण विमान – ललाट प्रक्षेपण विमान के लंबवत विमान(चित्र 3.4, ए)।

क्षैतिज प्रक्षेपण विमान – क्षैतिज प्रक्षेपण विमान के लंबवत विमान(चित्र 3.4, बी)।

प्रोफाइल-प्रोजेक्टिंग प्लेन – प्रक्षेपणों के प्रोफ़ाइल तल के लम्बवत तल.

प्रोजेक्शन प्लेन के समानांतर प्लेन कहलाते हैं स्तर के विमानया डबल प्रोजेक्टिंग प्लेन.

ललाट स्तर का विमान – ललाट प्रक्षेपण विमान के समानांतर विमान(चित्र 3.4, सी)।

क्षैतिज स्तर का विमान – क्षैतिज प्रक्षेपण विमान के समानांतर विमान(चित्र 3.4, डी)।

स्तर प्रोफ़ाइल विमान – प्रोफाइल प्रोजेक्शन प्लेन के समानांतर प्लेन(चित्र 3.4, ई)।

चित्र 3.4 - विशेष स्थिति वाले विमानों के प्लॉट

3.3। विमान में बिंदु और रेखा। एक बिंदु और एक सीधे विमान से संबंधित

एक बिंदु एक तल का है यदि वह उस तल में पड़ी किसी रेखा से संबंधित है(चित्र 3.5)।

एक रेखा एक तल से संबंधित होती है यदि उसमें तल के साथ कम से कम दो बिंदु उभयनिष्ठ हों।(चित्र 3.6)।

चित्र 3.5 - समतल में एक बिंदु से संबंधित

α = एम // एन

डी∈ एन⇒ डी∈ α

चित्र 3.6 - एक सीधे विमान से संबंधित

व्यायाम

चतुर्भुज द्वारा परिभाषित एक तल दिया गया है (चित्र 3.7, क)। वर्टेक्स के क्षैतिज प्रक्षेपण को पूरा करना आवश्यक है साथ.

ए	बी

चित्र 3.7 - समस्या का समाधान

समाधान :

1. ए बी सी डीसमतल को परिभाषित करने वाला एक समतल चतुर्भुज है।
2. इसमें विकर्ण बनाते हैं एसीऔर बी.डी(चित्र 3.7, बी), जो प्रतिच्छेदी रेखाएँ हैं, एक ही तल को भी परिभाषित करती हैं।
3. प्रतिच्छेदी रेखाओं की कसौटी के अनुसार, हम इन रेखाओं के प्रतिच्छेदन बिंदु के क्षैतिज प्रक्षेपण का निर्माण करते हैं - कइसके ज्ञात ललाट प्रक्षेपण के अनुसार: ए 2 सी 2 ∩ बी 2 डी 2 = के 2 .
4. सीधी रेखा के क्षैतिज प्रक्षेपण के साथ प्रक्षेपण कनेक्शन की रेखा को चौराहे पर पुनर्स्थापित करें बी.डी: विकर्ण प्रक्षेपण पर बी 1 डी 1 भवन को 1 .
5. द्वारा ए 1 को 1 हम विकर्ण का प्रक्षेपण करते हैं ए 1 साथ 1 .
6. बिंदु साथ 1 हम प्रोजेक्शन कनेक्शन लाइन के माध्यम से प्राप्त करते हैं जब तक कि यह विस्तारित विकर्ण के क्षैतिज प्रक्षेपण के साथ प्रतिच्छेद नहीं करता ए 1 को 1 .

3.4। विमान की मुख्य लाइनें

तल में अनंत रेखाएँ बनाई जा सकती हैं, लेकिन तल में कुछ विशेष रेखाएँ पड़ी होती हैं, जिन्हें कहते हैं विमान की मुख्य लाइनें (चित्र 3.8 - 3.11)।

सीधा स्तर या समतल समानांतरकिसी दिए गए तल में स्थित एक सीधी रेखा कहलाती है और प्रक्षेपण तलों में से एक के समानांतर होती है।

क्षैतिज या क्षैतिज स्तर की रेखा एच(पहला समांतर) एक सीधी रेखा है जो किसी दिए गए तल में पड़ी है और प्रक्षेपणों के क्षैतिज तल के समानांतर है (π 1)(चित्र 3.8, ए; 3.9)।

ललाट या सामने सीधा स्तर एफ(दूसरा समानांतर) एक सीधी रेखा है जो किसी दिए गए विमान में पड़ी है और अनुमानों के ललाट तल के समानांतर है (π 2)(चित्र 3.8, बी; 3.10)।

स्तर प्रोफ़ाइल लाइन पी(तीसरा समानांतर) एक सीधी रेखा है जो किसी दिए गए विमान में पड़ी है और अनुमानों के प्रोफाइल विमान के समानांतर है (π 3)(चित्र 3.8, सी; 3.11)।

चित्र 3.8 a - त्रिभुज द्वारा दिए गए तल में स्तर की क्षैतिज सीधी रेखा

चित्रा 3.8 बी - त्रिकोण द्वारा दिए गए विमान में स्तर की फ्रंटल लाइन

चित्रा 3.8 सी - त्रिकोण द्वारा निर्दिष्ट विमान में स्तर प्रोफ़ाइल रेखा

चित्रा 3.9 - निशान द्वारा निर्दिष्ट विमान में स्तर की क्षैतिज सीधी रेखा

चित्र 3.10 - निशान द्वारा निर्दिष्ट विमान में ललाट स्तर की रेखा

चित्रा 3.11 - निशान द्वारा निर्दिष्ट विमान में स्तर प्रोफाइल लाइन

3.5। एक सीधी रेखा और एक समतल की पारस्परिक स्थिति

किसी दिए गए समतल के संबंध में एक सीधी रेखा समानांतर हो सकती है और इसके साथ एक उभयनिष्ठ बिंदु हो सकता है, अर्थात यह प्रतिच्छेद करती है।

3.5.1। एक सीधे विमान की समानता

सीधे विमान के समांतरता का संकेत: एक रेखा एक समतल के समांतर होती है यदि वह उस तल की किसी रेखा के समांतर हो(चित्र 3.12)।

चित्र 3.12 - एक सीधे विमान की समानता

3.5.2। समतल के साथ रेखा का चौराहा

सामान्य स्थिति (चित्र 3.13) के विमान के साथ एक सीधी रेखा के चौराहे के बिंदु का निर्माण करने के लिए, यह आवश्यक है:

1. एक सीधी रेखा समाप्त करें एसहायक विमान में (एक सहायक विमान के रूप में, आंशिक स्थिति के विमानों को चुनना चाहिए);
2. दिए गए समतल α के साथ सहायक तल β के प्रतिच्छेदन रेखा का पता लगाएं;
3. दी गई रेखा का प्रतिच्छेदन बिंदु ज्ञात कीजिए एविमानों के चौराहे की एक पंक्ति के साथ एम.एन..

चित्र 3.13 - समतल के साथ एक सीधी रेखा के मिलन बिंदु का निर्माण

व्यायाम

दिया गया: प्रत्यक्ष अबसामान्य स्थिति में, समतल σ⊥π 1 । (चित्र 3.14)। एक रेखा के प्रतिच्छेदन बिंदु का निर्माण करें अबविमान σ के साथ।

समाधान :

1. विमान σ क्षैतिज रूप से प्रोजेक्ट कर रहा है, इसलिए, विमान σ का क्षैतिज प्रक्षेपण सीधी रेखा σ 1 (विमान का क्षैतिज निशान) है;
2. डॉट कोलाइन से संबंधित होना चाहिए अब ⇒ को 1 ∈ए 1 में 1 और एक दिया गया विमान σ ⇒ को 1 ∈σ 1 , इसलिए, को 1 अनुमानों के प्रतिच्छेदन बिंदु पर है ए 1 में 1 और σ 1;
3. ललाट प्रक्षेपण बिंदु कोप्रोजेक्शन कनेक्शन लाइन के माध्यम से हम पाते हैं: को 2 ∈ए 2 में 2 .

चित्र 3.14 - सामान्य स्थिति में एक रेखा का विशेष स्थिति के तल के साथ प्रतिच्छेदन

व्यायाम

दिया गया है: समतल σ = Δ एबीसी- सामान्य स्थिति, सीधी एफई(चित्र 3.15)।

एक रेखा के प्रतिच्छेदन बिंदु का निर्माण करना आवश्यक है एफईविमान σ के साथ।

ए	बी

चित्र 3.15 - समतल के साथ एक सीधी रेखा का प्रतिच्छेदन

1. आइए एक सीधी रेखा समाप्त करें एफईसहायक विमान में, जिसके लिए हम क्षैतिज रूप से प्रक्षेपित विमान α (चित्र 3.15, ए) का उपयोग करेंगे;
2. अगर α⊥π 1 , तो अनुमानों के विमान पर π 1 विमान α को एक सीधी रेखा में प्रक्षेपित किया जाता है (विमान απ 1 या α 1 का क्षैतिज निशान) के साथ मेल खाता है इ 1 एफ 1 ;
3. आइए विमान σ के साथ प्रोजेक्टिंग विमान α के चौराहे की रेखा (1-2) खोजें (इस तरह की समस्या का समाधान माना जाएगा);
4. रेखा (1-2) और दी गई रेखा एफईएक ही समतल α में लेटें और एक बिंदु पर प्रतिच्छेद करें क.

समस्या को हल करने के लिए एल्गोरिथम (चित्र 3.15, बी):

द्वारा एफईएक सहायक विमान α बनाएं:

3.6। प्रतिस्पर्धी बिंदुओं की विधि द्वारा दृश्यता का निर्धारण

इस रेखा की स्थिति का आकलन करते समय, यह निर्धारित करना आवश्यक है - प्रक्षेपण विमान π 1 या π 2 को देखते हुए, पर्यवेक्षकों के रूप में, रेखा के किस खंड का बिंदु हमारे करीब (आगे) है।

अंक जो विभिन्न वस्तुओं से संबंधित हैं, और प्रक्षेपण विमानों में से एक पर उनके प्रक्षेपण मेल खाते हैं (अर्थात, दो बिंदुओं को एक में प्रक्षेपित किया जाता है), इस प्रक्षेपण विमान पर प्रतिस्पर्धा कहलाते हैं.

प्रत्येक प्रक्षेपण विमान पर दृश्यता को अलग से परिभाषित करना आवश्यक है।

π 2 पर दृश्यता (चित्र 3.15)

हम π 2 - अंक 3 और 4 पर प्रतिस्पर्धा करने वाले बिंदु चुनते हैं। मान लीजिए कि बिंदु 3∈ है बीसी∈σ, बिंदु 4∈ एफई.

प्रक्षेपण तल π 2 पर बिंदुओं की दृश्यता निर्धारित करने के लिए, π 2 को देखते हुए क्षैतिज प्रक्षेपण तल पर इन बिंदुओं के स्थान को निर्धारित करना आवश्यक है।

π 2 को देखने की दिशा को एक तीर से दिखाया गया है।

बिंदु 3 और 4 के क्षैतिज प्रक्षेपण से, जब π 2 को देखते हैं, तो यह देखा जा सकता है कि बिंदु 4 1 3 1 की तुलना में पर्यवेक्षक के करीब स्थित है।

4 1 ∈इ 1 एफ 1 ⇒ 4∈एफई⇒ बिन्दु 4 रेखा पर स्थित π 2 पर दिखाई देगा एफई, इसलिए सीधी रेखा एफईमाना प्रतिस्पर्धी बिंदुओं की साइट पर विमान σ के सामने स्थित है और बिंदु तक दिखाई देगा क

π 1 पर दृश्यता

दृश्यता निर्धारित करने के लिए, हम उन बिंदुओं को चुनते हैं जो π 1 - अंक 2 और 5 पर प्रतिस्पर्धा करते हैं।

प्रक्षेपण तल π 1 पर बिंदुओं की दृश्यता निर्धारित करने के लिए, π 1 को देखते समय ललाट प्रक्षेपण तल पर इन बिंदुओं के स्थान को निर्धारित करना आवश्यक है।

π 1 को देखने की दिशा को एक तीर द्वारा दिखाया गया है।

बिंदु 2 और 5 के ललाट अनुमानों से, जब π 1 को देखते हुए, यह देखा जा सकता है कि बिंदु 2 2 5 2 की तुलना में पर्यवेक्षक के करीब स्थित है।

2 1 ∈ए 2 में 2 ⇒ 2∈अब⇒ बिन्दु 2, रेखा पर स्थित π 1 पर दिखाई देगा अब, इसलिए सीधी रेखा एफईमाना प्रतिस्पर्धी बिंदुओं के खंड पर विमान σ के नीचे स्थित है और बिंदु तक अदृश्य रहेगा कसमतल σ के साथ सीधी रेखा के प्रतिच्छेदन बिंदु हैं।

दो प्रतिस्पर्धी बिंदुओं का दृश्य वह होगा जो अधिक "Z" या (और) "Y" समन्वय के साथ होगा।

3.7। सीधे विमान की लंबवतता

सीधे विमान की लंबवतता का संकेत: एक रेखा एक तल के लंबवत होती है यदि वह दिए गए तल में स्थित दो प्रतिच्छेदी रेखाओं के लंबवत हो।

ए	बी

चित्र 3.16 - विमान के लिए एक सीधी रेखा लंबवत सेट करना

प्रमेय। यदि सीधी रेखा समतल के लंबवत है, तो आरेख पर: सीधी रेखा का क्षैतिज प्रक्षेपण समतल क्षैतिज के क्षैतिज प्रक्षेपण के लंबवत होता है, और सीधी रेखा का ललाट प्रक्षेपण ललाट के ललाट प्रक्षेपण के लंबवत होता है। (चित्र 3.16, बी)

एक विशेष मामले में प्रमेय को समकोण प्रक्षेपण प्रमेय के माध्यम से सिद्ध किया जाता है।

यदि विमान निशान द्वारा दिया जाता है, तो विमान के लंबवत सीधी रेखा के प्रक्षेपण विमान के संबंधित निशान (चित्रा 3.16, ए) के लंबवत होते हैं।

लाइन करने दो पीसमतल के लंबवत σ=Δ एबीसीऔर बिंदु से गुजरता है क.

1. आइए विमान σ=Δ में एक क्षैतिज और एक ललाट का निर्माण करें एबीसी : एक-1∈σ; एक-1// π 1; सी-2∈σ; सी-2//π 2।
2. बिंदु से पुनर्स्थापित करें कदिए गए विमान के लंबवत: पी 1⊥एच 1और p2⊥f2, या पी 1⊥απ 1 और p2⊥απ 2

3.8। दो विमानों की पारस्परिक स्थिति

3.8.1। समतल समानता

दो विमान समानांतर हो सकते हैं और एक दूसरे के साथ प्रतिच्छेद कर सकते हैं।

दो विमानों की समानता का संकेत: दो तल परस्पर समांतर होते हैं यदि एक तल की दो प्रतिच्छेदी रेखाएँ क्रमशः दूसरे तल की दो प्रतिच्छेदी रेखाओं के समांतर हों।

व्यायाम

सामान्य स्थिति में एक विमान दिया α=Δ एबीसीऔर डॉट एफ∉α (चित्र 3.17)।

डॉट के माध्यम से एफसमतल α के समांतर एक तल β खींचिए।

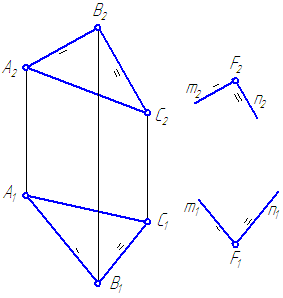
चित्र 3.17 - दिए गए के समानांतर एक विमान का निर्माण

समाधान :

समतल α की प्रतिच्छेदी रेखाओं के रूप में हम उदाहरण के लिए, त्रिभुज AB और BC की भुजाएँ लेते हैं।

1. डॉट के माध्यम से एफएक सीधी रेखा खींचना एम, समानांतर, उदाहरण के लिए, अब.
2. डॉट के माध्यम से एफ, या से संबंधित किसी भी बिंदु के माध्यम से एम, एक सीधी रेखा खींचो एन, समानांतर, उदाहरण के लिए, रवि, इसके अतिरिक्त एम∩एन = एफ.
3. β = एम∩एनऔर β // α परिभाषा के अनुसार।

3.8.2। हवाई जहाज़ का चौराहा

2 विमानों के प्रतिच्छेदन का परिणाम एक सीधी रेखा है। किसी समतल या अंतरिक्ष में किसी भी सीधी रेखा को विशिष्ट रूप से दो बिंदुओं द्वारा परिभाषित किया जा सकता है। इसलिए, दो विमानों के प्रतिच्छेदन की एक रेखा बनाने के लिए, दोनों विमानों के लिए दो सामान्य बिंदुओं को ढूंढना चाहिए और फिर उन्हें जोड़ना चाहिए।

उन्हें निर्दिष्ट करने के विभिन्न तरीकों के साथ दो विमानों के प्रतिच्छेदन के उदाहरणों पर विचार करें: निशान; तीन बिंदु जो एक सीधी रेखा पर स्थित नहीं हैं; समानांतर रेखाएं; प्रतिच्छेदन रेखाएँ, आदि।

व्यायाम

दो समतल α और β अनुरेखों द्वारा दिए गए हैं (चित्र 3.18)। विमानों के चौराहे की एक रेखा बनाएँ।

चित्र 3.18 - सामान्य स्थिति में विमानों का चौराहा, निशान द्वारा दिया गया

विमानों के चौराहे की एक पंक्ति बनाने की प्रक्रिया:

1. क्षैतिज निशानों का प्रतिच्छेदन बिंदु खोजें - यह बिंदु है एम(उसके अनुमान एम 1 और एम 2, जबकि एम 1 = एम, क्योंकि एम -समतल से संबंधित विशेष स्थिति का बिंदु π 1)।
2. ललाट के निशानों के प्रतिच्छेदन बिंदु का पता लगाएं - यह बिंदु है एन(उसके अनुमान एन 1 और एन 2, जबकि एन 2 = एन, क्योंकि एन-समतल से संबंधित विशेष स्थिति का बिंदु π 2).
3. प्राप्त बिंदुओं के अनुमानों को एक ही नाम से जोड़कर विमानों के चौराहे की एक रेखा का निर्माण करें: एम 1 एन 1 और एम 2 एन 2 .

एमएन- विमानों के चौराहे की रेखा।

व्यायाम

समतल σ = Δ एबीसी, विमान α क्षैतिज रूप से प्रोजेक्ट कर रहा है (α⊥π 1) ⇒α 1 विमान का क्षैतिज निशान है (चित्र 3.19)।

इन विमानों के प्रतिच्छेदन रेखा का निर्माण करें।

समाधान :

चूँकि समतल α भुजाओं को प्रतिच्छेद करता है अबऔर एसीत्रिकोण एबीसी, फिर चौराहे के बिंदु कऔर एलसमतल α के साथ इन पक्षों में से दोनों दिए गए विमानों के लिए सामान्य हैं, जो उन्हें जोड़कर, चौराहे की आवश्यक रेखा खोजने की अनुमति देगा।

पॉइंट्स को प्रोजेक्टिंग प्लेन के साथ लाइनों के चौराहे के बिंदुओं के रूप में पाया जा सकता है: बिंदुओं के क्षैतिज अनुमानों को खोजें कऔर एल, वह है क 1 और एल 1 , दिए गए समतल α के क्षैतिज ट्रेस (α 1) के चौराहे पर पक्षों के क्षैतिज अनुमानों के साथ Δ एबीसी: ए 1 में 1 और ए 1 सी 1। फिर, प्रोजेक्शन कनेक्शन की रेखाओं का उपयोग करते हुए, हम इन बिंदुओं के ललाट अनुमानों का पता लगाते हैं के2और एल 2 सीधी रेखाओं के ललाट अनुमानों पर अबऔर एसी. आइए एक ही नाम के अनुमानों को जोड़ते हैं: क 1 और एल 1 ; के2और एल 2. दिए गए विमानों के प्रतिच्छेदन की रेखा निर्मित है।

समस्या को हल करने के लिए एल्गोरिथम:

केएल- चौराहे की रेखा Δ एबीसीऔर σ (α∩σ = केएल).

चित्र 3.19 - सामान्य और विशेष स्थिति के विमानों का प्रतिच्छेदन

व्यायाम

दिया गया विमान α = m//n और विमान β = Δ एबीसी(चित्र 3.20)।

दिए गए समतलों के प्रतिच्छेदन रेखा का निर्माण करें।

समाधान :

1. दिए गए दोनों विमानों के लिए सामान्य बिंदुओं को खोजने और विमानों α और β के चौराहे की रेखा को परिभाषित करने के लिए, विशेष स्थिति के सहायक विमानों का उपयोग करना आवश्यक है।
2. इस तरह के विमानों के रूप में, हम विशेष स्थिति के दो सहायक विमानों का चयन करते हैं, उदाहरण के लिए: σ // τ; σ⊥π 2 ; τ⊥π 2 .
3. नए पेश किए गए विमान दिए गए प्रत्येक विमान α और β के साथ एक दूसरे के समानांतर सीधी रेखाओं के साथ प्रतिच्छेद करते हैं, क्योंकि σ // τ:

- विमानों α, σ और τ के चौराहे का नतीजा सीधी रेखाएं (4-5) और (6-7) हैं;

- विमानों के प्रतिच्छेदन का परिणाम β, σ और τ रेखाएं (3-2) और (1-8) हैं।

1. सीधी रेखाएँ (4-5) और (3-2) समतल σ में स्थित हैं; चौराहे का बिंदु एमएक साथ विमानों α और β में स्थित है, यानी इन विमानों के चौराहे की रेखा पर;
2. इसी तरह, हम बिंदु पाते हैं एन, विमानों α और β के लिए सामान्य।
3. बिंदियों को जोड़कर एमऔर एन, हम विमानों α और β के चौराहे की रेखा का निर्माण करते हैं।

चित्र 3.20 - सामान्य स्थिति में दो विमानों का चौराहा (सामान्य स्थिति)

समस्या को हल करने के लिए एल्गोरिथम:

व्यायाम

विमान α = Δ एबीसीऔर बी = ए//बी. दिए गए तलों के प्रतिच्छेदन रेखा की रचना कीजिए (चित्र 3.21)।

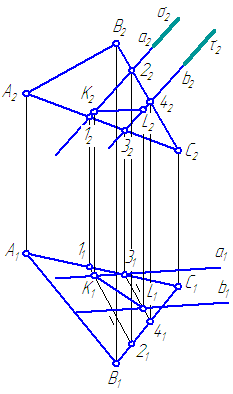
चित्र 3.21 विमानों के प्रतिच्छेदन की समस्या को हल करना

समाधान :

आइए निजी स्थिति के सहायक सेकेंडरी विमानों का उपयोग करें। हम उन्हें इस तरह से पेश करते हैं जैसे कि निर्माण की संख्या कम करना। उदाहरण के लिए, आइए रेखा को घेरते हुए समतल σ⊥π 2 का परिचय दें एसहायक तल में σ (σ∈ ए). विमान σ समतल α को सीधी रेखा (1-2) के साथ काटता है, और σ∩β= ए. अत: (1-2)∩ ए=क.

डॉट कोदोनों विमानों α और β के अंतर्गत आता है।

इसलिए बिंदु क, वांछित बिंदुओं में से एक है जिसके माध्यम से दिए गए विमानों α और β के चौराहे की रेखा गुजरती है।

α और β के प्रतिच्छेदन रेखा से संबंधित दूसरे बिंदु को खोजने के लिए, हम रेखा को समाप्त करते हैं बीसहायक विमान में τ⊥π 2 (τ∈ बी).

बिंदियों को जोड़कर कऔर एल, हम विमानों α और β के चौराहे की रेखा प्राप्त करते हैं।

3.8.3। परस्पर लंबवत विमान

विमान परस्पर लंबवत होते हैं यदि उनमें से एक दूसरे के लंबवत से होकर गुजरता है।

व्यायाम

एक विमान σ⊥π 2 और सामान्य स्थिति में एक सीधी रेखा को देखते हुए - डे(चित्र 3.22)

माध्यम से बनाना आवश्यक है डेविमान τ⊥σ।

समाधान ।

आइए एक लंब रेखा खींचें सीडीविमान के लिए σ - सी 2 डी 2 ⊥σ 2 (पर आधारित) ।

चित्र 3.22 - किसी दिए गए विमान के लम्बवत विमान का निर्माण

समकोण प्रक्षेपण प्रमेय के अनुसार सी 1 डी 1 प्रक्षेपण अक्ष के समानांतर होना चाहिए। प्रतिच्छेदन रेखाएँ सीडी∩डेसमतल τ को परिभाषित करें। तो, τ⊥σ।

समान तर्क, सामान्य स्थिति में विमान के मामले में।

व्यायाम

विमान α = Δ एबीसीऔर डॉट कविमान के बाहर α।

बिंदु से गुजरने वाले विमान β⊥α का निर्माण करना आवश्यक है क.

समाधान एल्गोरिथ्म(चित्र 3.23):

1. चलो एक क्षैतिज बनाते हैं एचऔर ललाट एफकिसी दिए गए विमान α में = Δ एबीसी;
2. डॉट के माध्यम से कएक लंबवत ड्रा करें बीविमान के लिए α (के अनुसार विमान प्रमेय के लंबवत: यदि रेखा समतल के लंबवत है, तो इसके प्रक्षेपण समतल में पड़े क्षैतिज और ललाट के तिरछे अनुमानों के लंबवत हैं:बी 2⊥f2; बी 1⊥एच 1;
3. हम विमान β को किसी भी तरह से सेट करते हैं, उदाहरण के लिए, β = ए∩बी, इस प्रकार, दिए गए तल के लम्बवत् तल का निर्माण किया जाता है: α⊥β।

चित्र 3.23 - दिए गए Δ के लंबवत समतल का निर्माण एबीसी

3.9। स्वतंत्र समाधान के लिए कार्य

1. विमान α = एम//एन(चित्र 3.24)। ह ज्ञात है कि क∈α.

बिंदु के ललाट प्रक्षेपण को प्लॉट करें को.

चित्र 3.24

2. एक खंड द्वारा दी गई एक सीधी रेखा के निशान बनाएँ सीबी, और उन चतुर्भुजों को निर्धारित करें जिनसे यह गुजरता है (चित्र 3.25)।

चित्र 3.25

3. समतल α⊥π 2 से संबंधित एक वर्ग के अनुमानों का निर्माण करें यदि इसका विकर्ण है एम.एन.//π 2 (चित्र 3.26)।

चित्र 3.26

4. एक आयत की रचना कीजिए ए बी सी डीबड़े पक्ष के साथ रविएक सीधी रेखा पर एम, इस शर्त के आधार पर कि इसके पक्षों का अनुपात 2 है (चित्र 3.27)।

चित्र 3.27

5. विमान α= ए//बी(चित्र 3.28)। समतल α के समानांतर और उससे 20 मिमी की दूरी पर एक विमान β का निर्माण करें।

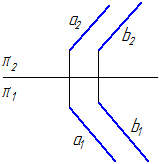
चित्र 3.28

6. समतल α=∆ एबीसीऔर डॉट डी डीसमतल β⊥α और β⊥π 1।

7. एक समतल α=∆ दिया है एबीसीऔर डॉट डीहवाई जहाज से बाहर। एक बिंदु के माध्यम से बनाएँ डीप्रत्यक्ष डे// α और डे// π 1।

समतल समानता। यदि एक तल की दो प्रतिच्छेदी रेखाएँ क्रमशः दूसरे तल की दो प्रतिच्छेदी रेखाओं के समांतर हों, तो ये तल समांतर होते हैं।
सबूत। होने देना एऔर बी- विमान डेटा, एक 1और एक 2- विमान में सीधी रेखाएँ ए, बिंदु A पर प्रतिच्छेद करता है, बी 1और बी 2विमान में उनके समानांतर रेखाएँ बी. आइए मान लें कि विमान एऔर बीसमानांतर नहीं, यानी वे किसी रेखा के साथ प्रतिच्छेद करते हैं साथ. सीधा ए 1 रेखा के समानांतर बी 1, इसलिए यह स्वयं समतल के समांतर है बी(एक सीधी रेखा और एक विमान के समानता का संकेत)। सीधा ए 2 रेखा के समानांतर बी 2,इसलिए यह विमान के समानांतर है। बी(एक सीधी रेखा और एक विमान के समानता का संकेत)। सीधा साथविमान के अंतर्गत आता है ए, तो कम से कम एक लाइन एक 1या एक 2रेखा पार करता है साथ,अर्थात्, इसके साथ एक सामान्य बिंदु है। लेकिन सीधा साथभी विमान के अंतर्गत आता है बी, जिसका अर्थ है कि रेखा को पार करना साथ,सीधा एक 1या एक 2विमान पार करता है बी, जो प्रत्यक्ष के बाद से नहीं हो सकता एक 1और एक 2विमान के समानांतर बी. यह इस प्रकार है कि विमान एऔर बीप्रतिच्छेद न करें, अर्थात वे समानांतर हैं।

प्रमेय 1 . यदि दो समानांतर समतल एक तीसरे के साथ प्रतिच्छेद करते हैं, तो प्रतिच्छेदन रेखाएँ समानांतर होती हैं।
सबूत। होने देना एऔर बीसमानांतर विमान हैं, और जी - विमान जो उन्हें काटता है। विमान एविमान के साथ प्रतिच्छेद करें जी एक सीधी रेखा में एक।विमान बीविमान के साथ प्रतिच्छेद करें जीएक सीधी रेखा में बी।चौराहे की रेखाएँ एऔर बीएक ही विमान में लेट जाओ जी और इसलिए या तो प्रतिच्छेदी या समानांतर रेखाएँ हो सकती हैं। लेकिन, दो समानांतर विमानों से संबंधित, उनके सामान्य बिंदु नहीं हो सकते। इसलिए, वे समानांतर हैं।

प्रमेय 2। दो समानांतर विमानों के बीच संलग्न समानांतर रेखाओं के खंड समान होते हैं।
सबूत। होने देना एऔर बीसमानांतर विमान हैं, और ए और बीसमानांतर रेखाएँ हैं जो उन्हें काटती हैं। सीधी रेखाओं द्वारा एऔर बीहम खर्च करेंगे विमान जी (ये रेखाएँ समानांतर हैं, इसलिएएक विमान को परिभाषित करें, और केवल एक)। विमान एविमान के साथ प्रतिच्छेद करें जी सीधी रेखा एबी . विमान बीविमान के साथ प्रतिच्छेद करें जीलाइन एसडी के साथ। पिछले प्रमेय के अनुसार, रेखा साथएक सीधी रेखा के समानांतर डी. प्रत्यक्ष ए,बी,अब और एसडी विमान के हैं जीइन रेखाओं से घिरा चतुर्भुज एक समांतर चतुर्भुज है (इसकी विपरीत भुजाएँ समानांतर हैं)। और चूँकि यह एक समांतर चतुर्भुज है, तो इसके विपरीत भुजाएँ समान हैं, अर्थात AD \u003d BC

समतलों के समांतरता, उसके गुणों और अनुप्रयोगों के संबंध पर विचार किया जाता है।

दो के स्थान का एक दृश्य प्रतिनिधित्व

प्लेन आसन्न दीवारों की सतहों, एक कमरे की छत और फर्श, बंक बेड, कागज की दो बंधी हुई चादरों के विमानों का उपयोग करके मॉडलिंग करते हैं

जादूगर, आदि (चित्र। 242-244)।

यद्यपि विभिन्न विमानों की सापेक्ष स्थिति के लिए अनंत संख्या में विकल्प हैं, जिनकी स्थापना और लक्षण वर्णन के लिए कोणों और दूरियों के माप को बाद में लागू किया जाएगा, हम पहले उन पर ध्यान केन्द्रित करेंगे जहां वर्गीकरण (साथ ही विमानों के साथ रेखाएं) उनके सामान्य बिंदुओं की संख्या पर आधारित है।

1. दो तलों में कम से कम तीन उभयनिष्ठ बिंदु होते हैं जो एक सीधी रेखा पर स्थित नहीं होते हैं। इस तरह के विमान मेल खाते हैं (स्वयंसिद्ध С 2 , §7)।

2. दो विमानों के सामान्य बिंदु एक सीधी रेखा पर स्थित होते हैं, जो इन विमानों के प्रतिच्छेदन की रेखा है (स्वयंसिद्ध C 3, § 7)। ये विमान प्रतिच्छेद करते हैं।

3. दोनों विमानों के सामान्य बिंदु नहीं हैं।

में इस मामले में उन्हें बुलाया जाता हैसमानांतर-

दो समतल समानांतर कहलाते हैं यदि उनके पास कोई उभयनिष्ठ बिंदु नहीं है।

समतलों की समानता को ||: α || द्वारा निरूपित किया जाता है β।

हमेशा की तरह, ज्यामितीय अवधारणाओं को प्रस्तुत करते समय,

उनके अस्तित्व को लेकर समस्या है। क्रॉस का अस्तित्व-

विमान अंतरिक्ष की एक विशेषता है,

और हमने इसे पहले भी कई बार इस्तेमाल किया है। कम स्पष्ट

समानांतर विमानों का अस्तित्व। कोई नहीं है

संदेह है कि, उदाहरण के लिए, विपरीत चेहरों के विमान

घन इसके समानांतर हैं, अर्थात वे प्रतिच्छेद नहीं करते हैं। लेकिन तुरंत

निश्चित रूप से, परिभाषा के अनुसार, इसे स्थापित करना असंभव है। हल करने के लिए

सवाल उठाया, साथ ही साथ अन्य मुद्दों से संबंधित

विमानों की समानता, समानता का संकेत होना जरूरी है।

संकेत खोजने के लिए, विमान पर विचार करना उचित है,

सीधी रेखाओं से "बुना"। जाहिर है, एक की प्रत्येक पंक्ति

समांतर विमानों को दूसरे के समानांतर होना चाहिए।

अन्यथा, विमानों का एक सामान्य बिंदु होगा। दोस्त-

क्या विमान β के समानांतर एक सीधे विमान α के समान हैं

ताकि समतल α और β समांतर हों? बिना शर्त

लेकिन, नहीं (इसे उचित ठहराएं!)। व्यावहारिक अनुभव यह दर्शाता है

ऐसी दो प्रतिच्छेदी रेखाएँ पर्याप्त हैं। पिन करने के लिए

मस्तूल पर जमीन के समानांतर एक मंच, इसे लगाने के लिए पर्याप्त है

दूसरे तल के समांतर हैं, तो ये तल समांतर हैं।

मान लीजिए कि समतल α की प्रतिच्छेदी रेखाएँ a और b समतल β के समांतर हैं। आइए सिद्ध करें कि समतल α और β विरोधाभास द्वारा समानांतर हैं। इसके लिए, हम मानते हैं कि समतल α और β सीधी रेखा के साथ प्रतिच्छेद करते हैं

टी (चित्र। 246)। रेखाएँ a और b धारणा द्वारा रेखा m को नहीं काट सकती हैं। हालाँकि, तब समतल α में एक बिंदु के माध्यम से दो सीधी रेखाएँ खींची जाती हैं जो रेखा m के साथ प्रतिच्छेद नहीं करती हैं, अर्थात इसके समानांतर। यह एक विरोधाभास है

और प्रमेय की उपपत्ति को पूरा करता है।

समतल संरचनाओं (कंक्रीट स्लैब, फर्श, डिस्क गोनियोमीटर, आदि) के क्षैतिज प्लेसमेंट के लिए विमानों के समांतरता के संकेत का उपयोग चौराहे की रेखाओं पर संरचना के विमान में रखे दो स्तरों का उपयोग करके किया जाता है। इस विशेषता के आधार पर, आप दिए गए विमान के समानांतर एक विमान बना सकते हैं।

कार्य 1। दिए गए विमान के बाहर स्थित एक बिंदु के माध्यम से, दिए गए एक के समानांतर एक विमान खींचें।

 मान लें कि समतल β और बिंदु M को तल के बाहर दिया गया है (चित्र 247, a)। बिंदु M के माध्यम से समतल β के समानांतर दो प्रतिच्छेदी रेखाएँ a और b खींचें। ऐसा करने के लिए, आपको विमान में दो इंटरसेक्टिंग लाइन सी और डी (चित्र। 247, बी) लेने की जरूरत है। फिर बिंदु M से क्रमशः c और d के समानांतर रेखाएँ a और b खींचें।

और (चित्र। 247, सी)।

प्रतिच्छेदी रेखाएँ a और b रेखा और समतल के समांतरता की कसौटी के अनुसार समतल β के समानांतर हैं (प्रमेय 1 §11)। वे विशिष्ट रूप से समतल α को परिभाषित करते हैं। सिद्ध कसौटी के अनुसार, α || β।

उदाहरण 1. एक घन ABCDA 1 B 1 C 1 D 1 दिया गया है, बिंदु M, N, P क्रमशः किनारों BC, B 1 C 1, A 1 D 1 के मध्य बिंदु हैं। विमानों की सापेक्ष स्थिति निर्धारित करें: 1) एबीबी 1 और पीएनएम; 2) एनएमए और ए 1 सी 1 सी; 3) ए 1 एनएम

और पीसी 1 सी; 4) एमएडी 1 और डीबी 1 सी।

 1) तलों की समानता (प्रमेय 1) के आधार पर तल ABB 1 और RNM (चित्र 248) समानांतर हैं। वास्तव में, रेखाएँ PN और NM प्रतिच्छेद करती हैं और समतल ABB 1 के समांतर हैं, रेखा और तल के समांतरता के संकेत द्वारा (§11 का प्रमेय 1), क्योंकि खंड PN और NM विपरीत भुजाओं के मध्यबिंदुओं को जोड़ते हैं वर्ग, इसलिए वे वर्गों की भुजाओं के समानांतर हैं:

पीएन || ए 1 बी 1, एनएम || 1 बी में

2) विमान NMA और A 1 C 1 C सीधी रेखा AA 1 (चित्र। 249) के साथ प्रतिच्छेद करते हैं। वास्तव में, रेखाएँ AA 1 और CC 1 समानांतर हैं, समानांतर रेखाओं (AA 1 || BB 1 , BB 1 || CC 1 ) के संकेत से। इसलिए, रेखा AA 1 समतल A 1 C 1 C में स्थित है। विमान एनएमए के लिए लाइन एए 1 से संबंधित एक समान तरीके से उचित है।

3) विमानों के समानता के आधार पर विमान ए 1 एनएम और पीसी 1 सी (छवि 250) समानांतर हैं। दरअसल, एनएम || 1 सी के साथ। इसलिए, रेखा NM समतल PC 1 C के समानांतर है। खंड PC 1 और A 1 N भी समानांतर हैं, क्योंकि चतुर्भुज PC 1 NA 1 एक समांतर चतुर्भुज है (A 1 P || NC 1, A 1 P = NC 1)। इस प्रकार, रेखा A 1 N समतल PC 1 C के समानांतर है। रेखाएँ A 1 N और NM प्रतिच्छेद करती हैं।

4) समतल MAD 1 और DB 1 C प्रतिच्छेद करते हैं (चित्र 251)। हालांकि उनके प्रतिच्छेदन की रेखा खींचना आसान नहीं है, लेकिन इस रेखा के एक बिंदु को इंगित करना मुश्किल नहीं है। वास्तव में, रेखाएँ A 1 D और B 1 C समानांतर हैं, क्योंकि चतुर्भुज A 1 B 1 CD एक समांतर चतुर्भुज है (A 1 B 1 \u003d AB \u003d CD, A 1 B 1 || AB, AB || CD) . इसलिए, रेखा A 1 D समतल DB 1 C से संबंधित है। रेखाएँ A 1 D और AD 1 समतल MAD 1 और DB 1 C के उभयनिष्ठ बिंदु पर प्रतिच्छेद करती हैं।

यदि एक तल की दो प्रतिच्छेदी रेखाएँ क्रमशः दूसरे तल की दो रेखाओं के समांतर हों, तो ये तल समांतर होते हैं।

एक सीधी रेखा और एक समतल (प्रमेय 1 §11) के समांतरता के चिह्न का उपयोग करके, यह स्थापित करना आसान है कि प्रमेय 1 की शर्त प्रमेय 1′ की स्थिति से अनुसरण करती है।

स्वाभाविक रूप से, समस्या 1 में दिए गए निर्माण की विशिष्टता के बारे में सवाल उठता है। चूंकि हमें इस संपत्ति का एक से अधिक बार उपयोग करना होगा, इसलिए हम इसे एक अलग प्रमेय के रूप में अलग करते हैं। हालाँकि, पहले एक और कथन पर विचार करें।

प्रमेय 2 (एक तिहाई द्वारा दो समानांतर विमानों के चौराहे पर)।

यदि दो समानांतर विमानों को तीसरे विमान द्वारा काट दिया जाता है, तो विमानों के प्रतिच्छेदन की रेखाएं समानांतर होती हैं।

 मान लें कि समांतर तल α, β और समतल γ उन्हें प्रतिच्छेद करते हैं (चित्र 252)। चौराहे की रेखाओं को निरूपित करें

ए और बी के माध्यम से। ये रेखाएँ समतल γ में स्थित हैं और प्रतिच्छेद नहीं करती हैं, क्योंकि समतल α और β का कोई उभयनिष्ठ बिंदु नहीं है। इसलिए प्रत्यक्ष

मेरे ए और बी समानांतर हैं।

प्रमेय 3 (किसी दिए गए के समानांतर एक विमान के अस्तित्व और विशिष्टता पर)।

किसी दिए गए विमान के बाहर एक बिंदु के माध्यम से दिए गए विमान के समानांतर केवल एक ही विमान होता है।

 ऐसे विमान का निर्माण समस्या 1 में किया गया है। हम विरोधाभास द्वारा निर्माण की विशिष्टता को सिद्ध करेंगे। आइए मान लें कि दो अलग-अलग विमान α और γ बिंदु एम के माध्यम से खींचे जाते हैं, पा-

समांतर विमान β (चित्र। 253), और सीधी रेखा एम उनके चौराहे की रेखा है। आइए हम बिंदु M से सीधी रेखा के साथ प्रतिच्छेद करता हुआ समतल δ खींचते हैं

मी और समतल β (यह कैसे किया जा सकता है?) ए और बी द्वारा निरूपित करें

विमानों α और γ के साथ विमान के चौराहे की रेखा, और c के माध्यम से - विमानों के चौराहे की रेखा δ और β (चित्र। 253)। प्रमेय 2 के अनुसार, और || साथ

और बी || साथ। यानी δ प्लेन में थ्रू

बिंदु M को रेखा c के समानांतर दो रेखाओं से गुजारा जाता है। विरोधाभास धारणा की गलतता को इंगित करता है।

समतलों के समांतरता के संबंध में अनेक गुण होते हैं जिनके समतलमिति में अनुरूप होते हैं।

प्रमेय 4 (समानांतर विमानों के बीच समानांतर रेखाओं के खंडों पर)।

समानांतर विमानों द्वारा काटे गए समानांतर रेखाओं के खंड एक दूसरे के बराबर होते हैं।

 दो समांतर विमानों α और β और सेगमेंट देंअब

और सीडी समानांतर रेखाएँ ए और डी, इन विमानों द्वारा काटी जाती हैं (चित्र। 254, ए)। आइए हम ए और डी (चित्र 254, बी) लाइनों के माध्यम से विमान γ को खींचते हैं। यह AC और BD के अनुदिश α और β समतलों को प्रतिच्छेदित करता है, जो प्रमेय 2 के अनुसार समानांतर हैं। इसलिए, चतुर्भुज ABCD एक समांतर चतुर्भुज है, इसकी सम्मुख भुजाएँ AC और BD बराबर हैं।

उपरोक्त संपत्ति से यह इस प्रकार है कि यदि हम विमान के सभी बिंदुओं से अलग रख दें

समतल के एक तरफ समान लंबाई के समानांतर खंड, फिर इन खंडों के सिरे दो समानांतर समतल बनाते हैं। यह इस संपत्ति पर है कि एक समानांतर चतुर्भुज का निर्माण खंडों के जमाव के माध्यम से आधारित है (चित्र। 255)।

प्रमेय 5 (विमानों के समानांतरवाद के संबंध की परिवर्तनशीलता पर)।

यदि दोनों में से प्रत्येक तल तीसरे के समांतर है, तो ये दोनों तल एक दूसरे के समांतर होंगे।

 विमानों α और β को विमान γ के समानांतर होने दें। चलिए मान लेते हैं

α तथा β समांतर नहीं हैं। तब समतल α और β का एक उभयनिष्ठ बिंदु होता है, और दो अलग-अलग तल इस बिंदु से गुजरते हैं और समतल γ के समानांतर होते हैं, जो प्रमेय 3 का खंडन करता है। इसलिए, समतल α और β के उभयनिष्ठ बिंदु नहीं हैं, अर्थात, वे हैं समानांतर।

प्रमेय 5 समतलों की समानता का एक और संकेत है। यह व्यापक रूप से ज्यामिति और व्यावहारिक गतिविधियों दोनों में उपयोग किया जाता है। उदाहरण के लिए, एक बहुमंजिला इमारत में, प्रत्येक मंजिल पर फर्श और छत के विमानों की समानता अलग-अलग मंजिलों पर उनकी समानता की गारंटी देती है।

समस्या 2। सिद्ध करें कि यदि एक रेखा एक समतल α को काटती है, तो यह समतल α के समानांतर प्रत्येक समतल को भी काटती है।

 मान लीजिए कि समतल α और β समानांतर हैं, और रेखा a समतल α को बिंदु A पर काटती है। आइए हम सिद्ध करें कि यह समतल को भी काटती है

β। चलिए मान लेते हैं कि ऐसा नहीं है। तब रेखा a समतल β के समांतर होती है। आइए हम रेखा a और समतल β (चित्र 256) के मनमाना बिंदु के माध्यम से विमान γ को खींचते हैं।

यह तल समानांतर समतल α और β को सीधी रेखाओं b और c के साथ काटता है। सह

प्रमेय 2 के अनुसार, बी || सी, यानी, बिंदु ए के माध्यम से विमान γ में दो रेखाएं ए और बी गुजरती हैं, लाइन सी के समानांतर . यह विरोधाभास कथन को सिद्ध करता है।

अपने लिए यह सिद्ध करने का प्रयास करें कि यदि कोई समतल α किसी तल β को काटता है, तो वह समतल β के समांतर प्रत्येक तल को भी प्रतिच्छेद करता है।

उदाहरण 2. चतुष्फलक ABCD में, बिंदु K, F, E किनारों के मध्यबिंदु हैं DA, DC, DB, और M और P क्रमशः चेहरों ABD और BCD के द्रव्यमान के केंद्र हैं।

1) केईएफ और एबीसी विमानों की सापेक्ष स्थिति निर्धारित करें;

डीईएफ और एबीसी।

2) AFB और KEC विमानों के प्रतिच्छेदन रेखा का निर्माण करें।

3) टेट्राहेड्रॉन के क्रॉस-सेक्शनल क्षेत्र को विमान एबीडी के समानांतर और बिंदु पी के माध्यम से गुजरने वाले विमान द्वारा खोजें, यदि टेट्राहेड्रॉन के सभी किनारों के बराबर हैं।

 आइए स्थिति के अनुरूप एक चित्र बनाएं (चित्र 257, ए)। 1) विमानों के समानता के आधार पर केईएफ और एबीसी समानांतर हैं (प्रमेय 1 '): केईएफ विमान के प्रतिच्छेदी रेखाएं केई और केएफ विमान एबीसी के प्रतिच्छेदी रेखाओं एबी और एसी के समानांतर हैं (द संबंधित की मध्य रेखाएँ

त्रिकोण बनाना)।

विमान DEF और ABC रेखा BC के साथ प्रतिच्छेद करते हैं, क्योंकि रेखा BC दोनों विमानों से संबंधित है, और वे संयोग नहीं कर सकते - बिंदु A, B, C, D एक ही विमान में नहीं हैं।

2) समतल AFB समतल KEC को बिंदु P वाली एक सीधी रेखा के साथ प्रतिच्छेद करता है, क्योंकि इन तलों में पड़ी रेखाएँ CE और BF समतल BCD में हैं और बिंदु P पर प्रतिच्छेद करती हैं। एक अन्य बिंदु समतल ACD (चित्र 257, b) में AF और CK की रेखाओं का प्रतिच्छेदन बिंदु Q है। जाहिर है, यह बिंदु एसीडी चेहरे के द्रव्यमान का केंद्र है। वांछित प्रतिच्छेदन रेखा PQ है।

3) विमानों के समांतरता के संकेत का उपयोग करके स्थिति में निर्दिष्ट अनुभाग का निर्माण करें। आइए हम क्रमशः DB और DA के समानांतर बिंदुओं P और Q से होकर रेखाएँ खींचते हैं (चित्र 257, c)। ये रेखाएँ बिंदु L पर खंड CD को काटती हैं। उत्तरार्द्ध त्रिभुज के द्रव्यमान के केंद्र की संपत्ति से अनुसरण करता है - यह त्रिभुज के मध्य को 2: 1 के अनुपात में विभाजित करता है, शीर्ष से गिनती करता है। यह थेल्स प्रमेय को लागू करने के लिए बनी हुई है। इस प्रकार विमान PLQ और BDA समानांतर हैं। वांछित खंड त्रिभुज एलएसएन है।

रचना के द्वारा, त्रिभुज BCD और SCL समानता गुणांक CE CP = 3 2 के साथ समान हैं। इसलिए एलएस = 3 2 बीडी। इसी प्रकार, द

समानताएँ जोड़ी जाती हैं: LN = 3 2 AD , NS = 3 2 AB । इसका तात्पर्य है कि त्रिभुज LSN और ABD समानता गुणांक 3 2 के समरूप हैं। समरूप त्रिभुजों के क्षेत्रफलों के गुणों से,

एस एलएनएस = 4 9 एस एबीडी। यह त्रिभुज ABD का क्षेत्रफल ज्ञात करना बाकी है। द्वारा-

चूंकि, धारणा के अनुसार, चतुष्फलक के सभी किनारे a के बराबर हैं, तो S ABD = 4 3 a 2 ।

वांछित क्षेत्र 3 1 3 a 2 है।

इस तथ्य पर ध्यान देना उचित है कि उत्तर केवल पहलू ABD के क्षेत्र पर निर्भर करता है। इसलिए, सभी किनारों की समानता इस क्षेत्र को खोजने का एक साधन मात्र है। इस प्रकार, इस समस्या को काफी हद तक सामान्यीकृत किया जा सकता है।

उत्तर। 1) केईएफ || एबीसी; 3) 3 1 3 ए 2।

 प्रश्नों को नियंत्रित करें

1. क्या यह सच है कि दो तल समांतर होते हैं यदि एक तल की प्रत्येक रेखा दूसरे तल के समांतर हो?

2. विमान α और β समानांतर हैं। क्या इन तलों में प्रतिच्छेदी रेखाएँ पड़ी हैं?

3. एक त्रिभुज की दो भुजाएँ किसी तल के समांतर हैं। क्या त्रिभुज की तीसरी भुजा इस समतल के समानांतर है?

4. एक समांतर चतुर्भुज की दो भुजाएँ किसी समतल के समानांतर होती हैं। क्या यह सत्य है कि समांतर चतुर्भुज का तल दिए गए तल के समांतर है?

5. क्या समांतर तलों द्वारा काटे गए दो सीधी रेखाओं के खंड असमान हो सकते हैं?

6. क्या घन का अनुप्रस्थ काट एक समद्विबाहु समलम्बाकार हो सकता है? क्या घन का खंड एक नियमित पेंटागन हो सकता है? क्या यह सच है कि एक ही रेखा के समांतर दो तल एक दूसरे के समांतर होते हैं?

समतल γ द्वारा समतल α और β के प्रतिच्छेदन की रेखाएँ एक दूसरे के समानांतर हैं। क्या समतल α और β समांतर हैं?

क्या एक घन के तीन फलक एक ही तल के समांतर हो सकते हैं?

ग्राफिक अभ्यास

1. चित्र 258 घन ABCDA 1 B 1 C 1 D 1 को दर्शाता है, बिंदु M , N , K , L , P संबंधित किनारों के मध्य बिंदु हैं। दिए गए नमूने के अनुसार तालिका में भरें, α और β विमानों की आवश्यक व्यवस्था का चयन करें।

आपसी

जगह

α || β α = β

α × β α || β α = β

2. अंजीर में। 259 चतुष्फलक ABCD को दर्शाता है, बिंदु K, F, M, N, Q संबंधित किनारों के मध्य बिंदु हैं। उल्लिखित करना:

1) बिंदु K से होकर गुजरने वाला समतल, समतल ABC के समानांतर;

2) विमान MNQ के समानांतर रेखा BD से गुजरने वाला एक विमान।

3. निर्धारित करें कि आकृति में दिखाए गए तीन बिंदुओं से गुजरने वाले विमान द्वारा आकृति का खंड क्या है।

कह 260, ए)-ई) और 261, ए)-डी)।

4. दिए गए आँकड़ों के अनुसार एक चित्र बनाएँ।

1) समांतर चतुर्भुज ABCD के शीर्ष से, दो समानांतर विमानों में से एक में स्थित, समानांतर रेखाएँ खींची जाती हैं जो क्रमशः A 1, B 1, C 1, D 1 बिंदुओं पर दूसरे विमान को काटती हैं।

2) त्रिभुज A 1 B 1 C 1 इसके समानांतर समतल α पर त्रिभुज ABC का प्रक्षेपण है। बिंदु M, BC का मध्य है, M 1 समतल α पर बिंदु M का प्रक्षेपण है।

207. घन ABCDA में 1 B 1 C 1 D 1 अंक O , O 1 चेहरों के केंद्र हैं ABCD और A 1 B 1 C 1 D 1 क्रमशः, M किनारे AB का मध्य बिंदु है।

1°) समतल MO 1 O की सापेक्ष स्थिति निर्धारित करें

और ADD 1 , ABD 1 और CO 1 C 1 ।

2°) समतल DCC 1 और रेखा MO 1 के प्रतिच्छेदन बिंदु और समतल MCC 1 और A 1 D 1 C 1 के प्रतिच्छेदन रेखा का निर्माण करें।

3) समतल AD 1 C 1 के समांतर समतल द्वारा घन का अनुप्रस्थ क्षेत्रफल ज्ञात करें और यदि घन का किनारा a है तो बिंदु O 1 से होकर गुजरें।

208. चतुष्फलक ABCD में बिंदु K, L, P क्रमशः ABD, BDC, ABC के फलकों के द्रव्यमान के केंद्र हैं, और M किनारे AD का मध्यबिंदु है।

1°) एसीडी विमानों की सापेक्ष स्थिति निर्धारित करें

और केएलपी; एमएलके और एबीसी।

2°) समतल ABC और रेखा ML के प्रतिच्छेदन बिंदु और समतल MKL और ABC के प्रतिच्छेदन रेखा का निर्माण करें।

3) टेट्राहेड्रॉन के क्रॉस-सेक्शनल क्षेत्र को बिंदु K, L और M से होकर गुजरने वाले विमान द्वारा सीधी रेखा AD के समानांतर खोजें, यदि टेट्राहेड्रॉन के सभी किनारे बराबर हैं।

209. एक घन ABCDA 1 B 1 C 1 D 1 दिया है। बिंदु L, M, M 1 क्रमशः किनारों AB, AD और A 1 D 1 के मध्य बिंदु हैं।

1°) तलों B 1 D 1 D की आपेक्षिक स्थिति निर्धारित करें

और एलएमएम1.

2) समतल ACC 1 के समानांतर बिंदु M से गुजरने वाले एक तल का निर्माण करें।

3) समतल CDD 1 के समानांतर बिंदु M 1 से गुजरने वाले तल द्वारा घन के एक खंड का निर्माण करें।

4) विमानों MA 1 IN 1 की सापेक्ष स्थिति निर्धारित करें

और सीडीएम1.

5) C 1 D 1 से गुजरने वाले समतल का निर्माण समतल CDM 1 के समानांतर करें।

210. एक नियमित चतुष्कोणीय पिरामिड SABCD में, सभी किनारे एक दूसरे के बराबर होते हैं। बिंदु L , M और N किनारों के मध्य बिंदु क्रमशः AS , BS , CS हैं।

1°) की सापेक्ष स्थिति निर्धारित करें: सीधी रेखाएँ LM और BC; सीधी रेखा एलएन और विमान एबीडी; विमान एलएमएन और बीडीसी।

2°) सिद्ध कीजिए कि त्रिभुज ABC और LMN समरूप हैं।

3) समतल AMN द्वारा पिरामिड के एक भाग का निर्माण करें; विमान एलएमएन; विमान एलबीसी।

4*) शीर्ष S से गुजरने वाले पिरामिड के किस भाग का क्षेत्रफल सबसे बड़ा है?

रेखाओं और विमानों की समानता

SABC चतुष्फलक में, सभी फलक नियमित त्रिभुज हैं। बिंदु एल, एम और एन क्रमश: एएस, बीएस, सीएस किनारों के मध्य बिंदु हैं। 1°) LM और BC रेखाओं की आपेक्षिक स्थिति निर्धारित करें। 2°) रेखा LN और समतल ABC की सापेक्ष स्थिति निर्धारित करें।

3) सिद्ध कीजिए कि त्रिभुज LMN और ABC समरूप हैं।

एक घन का एक भाग बनाएँ जो: 1°) एक समबाहु त्रिभुज हो; 2) एक पेंटागन।

217. एक चतुष्फलक के एक खंड का निर्माण करें जो एक समांतर चतुर्भुज है।

218°. सिद्ध कीजिए कि समान्तर चतुर्भुज के सम्मुख फलक समांतर होते हैं।

219. सिद्ध कीजिए कि दिए गए बिंदु से गुजरने वाली और दिए गए तल के समांतर सभी रेखाओं का समुच्चय दिए गए तल के समांतर तल बनाता है।

220. चार बिंदु A, B, C, D दिए गए हैं, जो एक ही तल में नहीं हैं। सिद्ध कीजिए कि रेखाओं AB और CD के समांतर प्रत्येक तल रेखाओं AC, AD, BD, BC को समांतर चतुर्भुज के शीर्षों पर प्रतिच्छेद करता है।

221. सिद्ध कीजिए कि एक समतल और एक रेखा जो इस तल से संबंधित नहीं है, एक दूसरे के समांतर होते हैं यदि वे दोनों एक ही तल के समांतर हों।

222. घन ABCDA 1 B 1 C 1 D 1 के विकर्णों के प्रतिच्छेदन बिंदु O के माध्यम से फलक ABCD के समांतर एक समतल खींचा जाता है। यह तल किनारों BB 1 और CC 1 को क्रमश: बिंदु M और N पर काटता है। सिद्ध कीजिए कि कोण MON एक समकोण है।

223. सिद्ध कीजिए कि दो तल एक दूसरे के समांतर होते हैं यदि और केवल यदि प्रत्येक रेखा जो एक तल को काटती है दूसरे को प्रतिच्छेद करती है।

224*. त्रिकोणीय पिरामिड SABC में AD और CE खंडों के माध्यम से, जहाँ D SB का मध्य है, और E SA का मध्य है, पिरामिड के खंडों को एक दूसरे के समानांतर खींचें।

225. ज्यामितीय स्थानों का पता लगाएं:

1) दिए गए दो समांतर तलों पर सिरों वाले सभी खंडों के मध्य बिंदु; 2*) दो दी गई प्रतिच्छेदी रेखाओं पर सिरों वाले खंडों के मध्य बिंदु।

226*. समतल α में स्थित त्रिभुज ABC की भुजा AB समतल β के समांतर है। एक समबाहु त्रिभुज A 1 B 1 C 1 समतल β पर त्रिभुज ABC का एक समानांतर प्रक्षेपण है; एबी = 5, बीसी = 6, एसी = 9।

1) रेखाओं AB और A 1 B 1 की सापेक्ष स्थिति निर्धारित करें,

बीसी और बी1 सी1, ए1 सी1 और एसी।

2) त्रिभुज A 1 B 1 C 1 का क्षेत्रफल ज्ञात कीजिए।

227*. दो प्रतिच्छेदी रेखाएँ दी गई हैं। अंतरिक्ष में सभी बिंदुओं का सेट निर्दिष्ट करें जिसके माध्यम से दो दी गई रेखाओं में से प्रत्येक को प्रतिच्छेद करने वाली रेखा खींचना संभव है।

मूल परिभाषा

दो विमानों को कहा जाता है

समानांतर हैं,

यदि उनके पास सामान्य बिंदु नहीं हैं।

मुख्य कथन

समांतर का चिह्न यदि समतल के एक तल की दो रेखाओं के दो प्रतिच्छेद क्रमशः दूसरे तल की दो रेखाओं के समांतर हों, तो ये तल

हड्डियाँ समानांतर होती हैं।

Ne के बारे में प्रमेय- यदि दो समांतर तलों के दो समांतर-प्रतिच्छेदों को किसी तल द्वारा किसी तीसरे तल द्वारा प्रतिच्छेदित किया जाए, तो तल के तीसरे प्रतिच्छेदन की रेखाएँ

वे समानांतर हैं।

ए α, बी α, ए × बी, सी β, डी β, ए || सी, बी || dα || β

α || β, a = γ∩α, b = γ∩β a || बी

मा

β: α || बी, एम बी

विषयगत के लिए तैयार हो रही है

किसके लिए "रेखाओं और विमानों की समानता" विषय पर मूल्यांकन

आत्म-नियंत्रण के लिए कार्य

1. चार बिंदु एक ही तल के नहीं हैं। क्या उनमें से कोई तीन एक ही रेखा पर स्थित हो सकते हैं?

2. क्या तीन भिन्न तलों में ठीक दो बिंदु उभयनिष्ठ हो सकते हैं?

3. क्या दो प्रतिच्छेदी रेखाएँ एक साथ तीसरी रेखा के समानांतर हो सकती हैं?

4. क्या यह सच है कि सीधेए और बी समानांतर नहीं हैं यदि ए और बी के समानांतर कोई रेखा सी नहीं है?

5. क्या समान खंडों में असमान प्रक्षेपण हो सकते हैं?

6. क्या किरण एक रेखा का समानांतर प्रक्षेपण हो सकता है?

7. क्या वर्ग, घन का प्रतिबिम्ब हो सकता है?

8. क्या यह सच है कि अंतरिक्ष में दिए गए बिंदु के माध्यम से दी गई रेखा के समानांतर केवल एक ही तल हो सकता है?

9. क्या किसी दिए गए बिंदु के समानांतर दो दिए गए विमानों के समानांतर एक रेखा खींचना संभव है जिसमें यह बिंदु नहीं है?

10. क्या दो प्रतिच्छेदी रेखाओं के माध्यम से समानांतर समतल बनाना संभव है?

आत्म-नियंत्रण के लिए कार्यों के उत्तर

नमूना जांच

दो समांतरोग्राम एबीसीडी और एबीसी 1 डी 1 अलग-अलग विमानों में स्थित हैं।

1°) रेखाओं CD और C 1 D 1 की आपेक्षिक स्थिति निर्धारित करें।

2°) रेखा C 1 D 1 और समतल की सापेक्ष स्थिति निर्धारित करें

3°) समतल DD 1 C 1 और BCC 1 के प्रतिच्छेदन रेखा का निर्माण करें।

4 °) ADD 1 और BCC 1 विमानों की सापेक्ष स्थिति निर्धारित करें।

5) बिंदु M के माध्यम से, खंड AB को 2: 1 के अनुपात में विभाजित करते हुए, बिंदु A से गिनती करते हुए, एक समतल α को समतल C 1 BC के समानांतर खींचें। 6) समतल α के साथ रेखा AC के प्रतिच्छेदन बिंदु का निर्माण करें और वह अनुपात ज्ञात करें जिसमें यह बिंदु खंड AC को विभाजित करता है।

अंतरिक्ष में सीधी रेखाओं और तलों की पारस्परिक व्यवस्था

त्रिकोणमितीय

आप पहले ही ज्यामिति के पाठों में त्रिकोणमितीय फलनों के बारे में पढ़ चुके हैं। अब तक, उनके अनुप्रयोग मुख्य रूप से त्रिभुजों के समाधान तक ही सीमित रहे हैं, अर्थात यह त्रिभुज के कुछ तत्वों को दूसरों से खोजने के बारे में था। गणित के इतिहास से ज्ञात होता है कि त्रिकोणमिति का उद्भव लंबाई और कोणों के मापन से जुड़ा है। बहरहाल, अब गुंजाइश है

उसका पुरातनता की तुलना में अनुप्रयोग बहुत व्यापक हैं।

शब्द "त्रिकोणमिति" ग्रीक τριγωνον से आया है

(त्रिकोण) - एक त्रिकोण और μετρεω (मेट्रो) - मैं मापता हूं, बदलता हूं

रयू। इसका शाब्दिक अर्थ है त्रिभुजों की माप।

में यह अध्याय ज्यामिति पाठ्यक्रम से आपके लिए पहले से ज्ञात सामग्री को व्यवस्थित करता है, त्रिकोणमितीय कार्यों का अध्ययन जारी रखता है और आवधिक प्रक्रियाओं को चिह्नित करने के लिए उनके अनुप्रयोग, विशेष रूप से, घूर्णी गति, दोलन संबंधी प्रक्रियाएं, आदि।

त्रिकोणमिति के अधिकांश अनुप्रयोग सटीक आवधिक प्रक्रियाओं से संबंधित हैं, अर्थात ऐसी प्रक्रियाएँ जो नियमित अंतराल पर दोहराई जाती हैं। सूर्य का उदय और अस्त होना, ऋतुओं का परिवर्तन, चक्र का घूमना ऐसी प्रक्रियाओं के सबसे सरल उदाहरण हैं। यांत्रिक और विद्युत चुम्बकीय दोलन भी आवधिक प्रक्रियाओं के महत्वपूर्ण उदाहरण हैं। इसलिए, आवधिक प्रक्रियाओं का अध्ययन एक महत्वपूर्ण कार्य है। और इसके समाधान में गणित की भूमिका निर्णायक होती है।

"त्रिकोणमितीय फ़ंक्शंस" विषय का अध्ययन करने के लिए तैयार होना

त्रिकोण के कोणों के त्रिकोणमितीय कार्यों की परिभाषाओं और गुणों को दोहराकर और समकोण और मनमाने त्रिकोण दोनों को हल करने के लिए उनके अनुप्रयोगों का अध्ययन शुरू करने की सलाह दी जाती है।

एक आयताकार के कोणों की साइन, कोसाइन, स्पर्शरेखा, स्पर्शरेखा

त्रिकोण

तालिका 24

एक तीव्र कोण की साइन कर्ण के विपरीत पैर का अनुपात है:

sinα = एक सी।

एक तीव्र कोण का कोज्या कर्ण के निकटवर्ती पैर का अनुपात है:

cosα = बी सी।

एक तीव्र कोण का स्पर्शरेखा विपरीत पैर के आसन्न पैर का अनुपात है:

टीजीए = ए बी।

एक तीव्र कोण का कोटिस्पर्श आसन्न पैर के विपरीत के अनुपात का अनुपात है:

सीटीजीए = ए बी।

साइन, कोसाइन, स्पर्शरेखा, 0° से 180° कोणों की कोटिस्पर्श रेखा

तालिका 25

sin α = R y ; cosα = आर एक्स;

टीजीए = एक्स वाई; ctgα = एक्स वाई.

(एक्स; पर) - बिंदु निर्देशांक एऊपरी अर्धवृत्त पर स्थित, α - त्रिज्या द्वारा गठित कोण ओएधुरी के साथ घेरा एक्स.

साइन, कोसाइन, स्पर्शरेखा, कोटेंगेंट मान

कुछ कोने

तालिका 26

कोना टी

मनमाना त्रिभुजों को हल करना

तालिका 27

ज्या प्रमेय

त्रिभुज की भुजाएँ विपरीत कोणों की ज्या के समानुपाती होती हैं:

पाप एα = पाप बीβ = पाप सीγ .

कोसाइन प्रमेय

त्रिभुज की एक मनमाना भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है, इन भुजाओं के उत्पाद को उनके बीच के कोण के कोसाइन से दोगुना किए बिना:

सी2 = ए2 + बी2 − 2 अबओल γ ,बी2 = ए2 + सी2 − 2 एसीओल β , ए2 = बी2 + सी2 − 2 ईसा पूर्वओल α .

किसी त्रिभुज का क्षेत्रफल उसकी दो भुजाओं के गुणनफल और उनके बीच के कोण की ज्या का आधा होता है:

एस= 1 2 अबपापγ = 1 2 एसीपापβ = 1 2 ईसा पूर्वपापα .

बुनियादी त्रिकोणमितीय पहचान

5. एक स्वेच्छ समकोण त्रिभुज के तीव्र कोणों की ज्याओं के योग की तुलना करें (हम इसे निरूपित करते हैंए) एकता के साथ।

< 1. बी।ए= 1.

> 1. जी।तुलना करना असंभव है। आरोही क्रम में व्यवस्थित करें: ए= पाप 30°, बी= कॉस 30°,

= टीजी 30 डिग्री।

< बी< सी. बी।ए< सी< बी. में।सी< ए< बी. जी।बी< ए< सी.

कम्प्यूटेशनल साधनों के बिना तुलना करें तीव्र कोण α और β, 7.

15. बिंदु निर्देशांक निर्दिष्ट करेंएत्रिज्या 1 के एक वृत्त पर स्थित है (चित्र देखें।)।

(−1; 0). बी।(1; 0).

(0; − 1). जी।(0; 1).एक।में।

किसी भी तकनीकी संचालन को एक निश्चित सटीकता के साथ किया जा सकता है, जिसका अर्थ है कि प्रसंस्करण के परिणामस्वरूप प्राप्त भाग के आयाम आदर्श नहीं होंगे, वे एक निश्चित सीमा में उतार-चढ़ाव कर सकते हैं। विधानसभा की शर्तों को पूरा करने और दी गई शर्तों के तहत भाग के विश्वसनीय संचालन को सुनिश्चित करने के लिए, स्वीकार्य अंतराल निर्धारित करना आवश्यक है जिसमें अंतिम आकार गिरना चाहिए। यह अंतराल न केवल रैखिक या व्यासीय आयामों को नियंत्रित कर सकता है, बल्कि सतहों के आकार या सापेक्ष स्थिति को भी नियंत्रित कर सकता है।

असेंबली स्थितियों और तंत्र में भाग की विशेषताओं के आधार पर डिज़ाइनर द्वारा आकार और स्थान सहनशीलता को असाइन किया जाता है।

प्रपत्र सहिष्णुता के प्रकार

रूप सहिष्णुताफॉर्म के विचलन का अधिकतम स्वीकार्य मूल्य कहा जाता है।

प्रपत्र सहिष्णुता क्षेत्र- यह एक विमान या अंतरिक्ष में एक क्षेत्र है, जिसके अंदर विचाराधीन तत्व के सभी बिंदु सामान्यीकृत क्षेत्र के भीतर स्थित होने चाहिए, जिसकी चौड़ाई या व्यास सहिष्णुता मूल्य और वास्तविक तत्व के सापेक्ष स्थान से निर्धारित होता है आसन्न तत्व द्वारा।

प्रपत्र विचलन और सहनशीलता

आकार विचलन के लिए निम्नलिखित सहनशीलता हैं:

• विमान में सीधेपन से विचलन
• उत्तल
• अवतलता
• समतलता और समतलता सहिष्णुता से विचलन
• उत्तल
• अवतलता
• गोलाई विचलन और गोलाई सहिष्णुता
• ओवेलिटि
• काटना
• बेलनाकार विचलन और बेलनाकार सहिष्णुता
• बेलनाकार सतह के अनुदैर्ध्य खंड के प्रोफ़ाइल का विचलन और सहनशीलता
• अनुदैर्ध्य खंड के प्रोफ़ाइल का विचलन
• टेपर
• बैरल का आकार
• काठी का आकार

अनुमेय विचलन विशेष प्रतीकों द्वारा इंगित किए जाते हैं।

स्थान सहिष्णुता के प्रकार

स्थान सहिष्णुता- एक सीमा जो स्थान के विचलन के स्वीकार्य मूल्य को सीमित करती है।

स्थान सहिष्णुता और अभिविन्यास सहिष्णुता हैं।

स्थान सहिष्णुता क्षेत्र- एक विमान या अंतरिक्ष में एक क्षेत्र, जिसके अंदर एक आसन्न तत्व या समरूपता का एक विमान होना चाहिए, एक अक्ष, सामान्यीकृत क्षेत्र के भीतर एक केंद्र, जिसका व्यास या चौड़ाई सहिष्णुता मूल्य और रिश्तेदार द्वारा निर्धारित किया जाता है स्थिति विचाराधीन तत्व के नाममात्र स्थान से निर्धारित होती है।

विचलन और स्थान सहिष्णुता

निम्नलिखित प्रकार के स्थान सहिष्णुता हैं:

• समानांतरवाद विचलन और समानांतरवाद सहिष्णुता
• विचलन और लम्बवत सहिष्णुता
• विचलन और झुकाव सहिष्णुता
• विचलन और संरेखण सहिष्णुता
• त्रिज्या सहिष्णुता
• विचलन और समरूपता सहिष्णुता
• स्थितीय विचलन और स्थितीय सहिष्णुता
• व्यास के संदर्भ में सहिष्णुता
• त्रिज्या सहिष्णुता
• चौराहों से विचलन और कुल्हाड़ियों के प्रतिच्छेदन की सहनशीलता
• व्यास के संदर्भ में सहिष्णुता
• त्रिज्या सहिष्णुता

कुल सहनशीलता

कई प्रकार के कुल आकार और स्थान सहिष्णुता हैं।

• रेडियल रनआउट
• पूर्ण रेडियल रनआउट
• फेस रनआउट
• पूर्ण अक्षीय अपवाह
• एक निश्चित दिशा में रनआउट करें
• किसी दिए गए प्रोफ़ाइल के आकार का विचलन और सहनशीलता
• किसी दिए गए सतह के आकार का विचलन और सहनशीलता

इन सहनशीलता को प्रतीकों द्वारा दर्शाया गया है।

ड्राइंग में आकार और स्थान की सहनशीलता का पदनाम

आकृतियों में आकार और स्थान की सहनशीलता को एक फ्रेम के रूप में दर्शाया गया है, जिसे कई भागों में विभाजित किया गया है। पहले भाग में, सहिष्णुता का एक ग्राफिक पदनाम दर्शाया गया है, दूसरे भाग में - सहिष्णुता का संख्यात्मक मान, तीसरे और बाद में - एक या अधिक आधारों का अक्षर पदनाम।

सहनशीलता के आधार के अभाव में, फ्रेम में केवल दो भाग होते हैं। आकृति और स्थान सहिष्णुता फ्रेम के उदाहरण चित्र में दिखाए गए हैं।

बाईं ओर का आंकड़ा एक स्थान सहिष्णुता (समानता से अनुमेय विचलन) के साथ दाईं ओर एक आकार सहिष्णुता (सीधापन से अनुमेय विचलन) के साथ एक फ्रेम दिखाता है।

फ्रेम पतली रेखाओं से बना है। फ़्रेम में टेक्स्ट की ऊंचाई आयाम संख्या के फ़ॉन्ट आकार के बराबर होनी चाहिए। एक तीर के साथ समाप्त होने वाली रेखा सहिष्णुता फ्रेम से सतह या नेता तक खींची जाती है।

सहिष्णुता के संख्यात्मक मूल्य से पहले, संकेतों को इंगित किया जा सकता है:

• च - यदि एक बेलनाकार या वृत्ताकार सहिष्णुता क्षेत्र एक व्यास द्वारा इंगित किया गया है
• R - यदि एक बेलनाकार या वृत्ताकार क्षेत्र को एक त्रिज्या द्वारा इंगित किया जाता है
• टी - यदि कुल्हाड़ियों, समरूपता के प्रतिच्छेदन के लिए सहिष्णुता क्षेत्र, दो समानांतर रेखाओं या विमानों में व्यास के संदर्भ में सीमित है।
• टी / 2 - टी के समान मामले में, केवल त्रिज्या अभिव्यक्ति में
• क्षेत्र - एक गोलाकार सहिष्णुता क्षेत्र के लिए।

यदि सहिष्णुता को पूरी सतह पर नहीं, बल्कि केवल एक निश्चित क्षेत्र पर लागू किया जाना चाहिए, तो इसे बिंदीदार रेखा के साथ डैश द्वारा इंगित किया जाता है।

एक तत्व के लिए, कई सहिष्णुता निर्दिष्ट की जा सकती हैं, इस मामले में फ्रेम एक के ऊपर एक खींचे जाते हैं।

अतिरिक्त जानकारी फ़्रेम के ऊपर या नीचे दिखाई दे सकती है।

आकार और स्थान की सहनशीलता के बारे में जानकारी में निर्दिष्ट किया जा सकता है।

GOST 25069-81 के अनुसार अनिर्दिष्ट संरेखण सहनशीलता।

आश्रित सहनशीलता

आश्रित स्थान सहनशीलता निम्नलिखित प्रतीक द्वारा इंगित की जाती है।

यह प्रतीक सहिष्णुता के संख्यात्मक मान के बाद रखा जा सकता है, यदि आश्रित सहिष्णुता संबंधित तत्व के वास्तविक आयामों से संबंधित है। साथ ही, प्रतीक को अक्षर पदनाम के बाद रखा जा सकता है (यदि यह अनुपस्थित है, तो फ्रेम के तीसरे क्षेत्र में) यदि आश्रित सहिष्णुता आधार तत्व के वास्तविक आयामों से संबंधित है।

आकार और स्थान सहनशीलता असाइन करें

जितना अधिक सटीक रूप से एक भाग बनाया जाता है, उसके निर्माण और आयामी नियंत्रण के लिए उतने ही सटीक उपकरणों की आवश्यकता होगी। इससे इसकी कीमत अपने आप बढ़ जाएगी। यह पता चला है कि एक हिस्से के निर्माण की लागत काफी हद तक इसके निर्माण में आवश्यक सटीकता पर निर्भर करती है। इसका मतलब यह है कि डिजाइनर को केवल उन सहनशीलता को निर्दिष्ट करना चाहिए जो असेंबली और आंदोलन के विश्वसनीय संचालन के लिए वास्तव में आवश्यक हैं। संग्रह और प्रदर्शन की शर्तों के आधार पर अनुमेय अंतराल भी निर्दिष्ट किए जाने चाहिए।

प्रपत्र सहिष्णुता संख्यात्मक मान

सटीकता वर्ग के आधार पर, फॉर्म टॉलरेंस के मानक मान निर्धारित किए जाते हैं।

सपाटपन और सीधापन सहनशीलता

इस मामले में, नाममात्र आकार को सामान्यीकृत खंड की नाममात्र लंबाई माना जाता है।

गोलाई, बेलनाकार, अनुदैर्ध्य खंड प्रोफ़ाइल की सहनशीलता

ये सहनशीलता उन मामलों में निर्दिष्ट की जाती हैं जहां उन्हें आकार सहिष्णुता से कम होना चाहिए।

नाममात्र आकार नाममात्र सतह व्यास है।

लंबवतता, समानता, झुकाव, अक्षीय रनआउट के लिए सहनशीलता

समांतरता, लंबवतता, झुकाव के लिए सहिष्णुता निर्दिष्ट करते समय नाममात्र आकार को नाममात्र सामान्यीकृत अनुभाग या संपूर्ण नियंत्रित सतह की नाममात्र लंबाई के रूप में समझा जाता है।

रेडियल रनआउट, समरूपता, व्यास के संदर्भ में कुल्हाड़ियों के चौराहे की समाक्षीयता की सहनशीलता

रेडियल रनआउट सहनशीलता निर्दिष्ट करते समय, नाममात्र आकार को प्रश्न में सतह का नाममात्र व्यास माना जाता है।

समरूपता के लिए सहनशीलता निर्दिष्ट करने के मामले में, संरेखण की धुरी के चौराहे, नाममात्र आकार सतह का नाममात्र व्यास या सतहों के बीच नाममात्र आकार है जो प्रश्न में तत्व बनाते हैं।

हर कोई जिसने कभी अध्ययन किया है या वर्तमान में स्कूल में पढ़ रहा है, को शिक्षा मंत्रालय द्वारा विकसित कार्यक्रम में शामिल विषयों का अध्ययन करने में विभिन्न कठिनाइयों का सामना करना पड़ा है।

आपको किन कठिनाइयों का सामना करना पड़ता है

भाषाओं का अध्ययन मौजूदा व्याकरणिक नियमों के संस्मरण और उनके मुख्य अपवादों के साथ है। शारीरिक शिक्षा के लिए छात्रों से महान गणना, अच्छे शारीरिक आकार और महान धैर्य की आवश्यकता होती है।

हालांकि, सटीक विषयों के अध्ययन में आने वाली कठिनाइयों की तुलना में कुछ भी नहीं है। बीजगणित, जिसमें प्रारंभिक समस्याओं को हल करने के जटिल तरीके शामिल हैं। भौतिक कानूनों के सूत्रों के एक समृद्ध सेट के साथ भौतिकी। ज्यामिति और उसके खंड, जो जटिल प्रमेयों और स्वयंसिद्धों पर आधारित हैं।

एक उदाहरण स्वयंसिद्ध है जो विमानों के समानांतरवाद के सिद्धांत की व्याख्या करता है, जिसे याद रखना चाहिए, क्योंकि वे रूढ़िवादिता पर स्कूल के पाठ्यक्रम के पूरे पाठ्यक्रम को रेखांकित करते हैं। आइए यह पता लगाने की कोशिश करें कि यह कितना आसान और तेज़ किया जा सकता है।

उदाहरण के द्वारा समानांतर विमान

विमानों की समानता को इंगित करने वाला स्वयंसिद्ध इस प्रकार है: " किन्हीं भी दो तलों को समानांतर तभी माना जाता है जब उनमें उभयनिष्ठ बिंदु न हों।”, अर्थात वे एक दूसरे के साथ प्रतिच्छेद नहीं करते हैं। इस तस्वीर की अधिक विस्तार से कल्पना करने के लिए, प्राथमिक उदाहरण के रूप में, हम एक इमारत में छत और फर्श या विपरीत दीवारों के अनुपात का हवाला दे सकते हैं। यह तुरंत स्पष्ट हो जाता है कि क्या मतलब है, और इस तथ्य की भी पुष्टि की जाती है कि सामान्य स्थिति में ये विमान कभी भी प्रतिच्छेद नहीं करेंगे।

एक अन्य उदाहरण एक डबल-चकाचले खिड़की है, जहां कांच की चादरें विमानों के रूप में कार्य करती हैं। वे भी किसी भी परिस्थिति में एक दूसरे के साथ प्रतिच्छेदन बिंदु नहीं बनाएंगे। इसके अलावा, आप बुकशेल्फ़, एक रूबिक क्यूब, जहां प्लेन इसके विपरीत चेहरे हैं, और रोजमर्रा की जिंदगी के अन्य तत्व जोड़ सकते हैं।

विचार किए गए विमानों को दो सीधी रेखाओं "||" के रूप में एक विशेष चिन्ह के साथ नामित किया गया है, जो स्पष्ट रूप से विमानों की समानता को दर्शाता है। इस प्रकार, वास्तविक उदाहरणों को लागू करके, विषय की स्पष्ट धारणा बना सकते हैं, और इसलिए, अधिक जटिल अवधारणाओं पर विचार करने के लिए आगे बढ़ सकते हैं।

समानांतर विमानों का सिद्धांत कहाँ और कैसे लागू होता है?

स्कूल ज्यामिति पाठ्यक्रम का अध्ययन करते समय, छात्रों को बहुमुखी कार्यों से निपटना पड़ता है, जहाँ अक्सर सीधी रेखाओं की समानता, एक सीधी रेखा और एक दूसरे के बीच एक विमान या एक दूसरे पर विमानों की निर्भरता का निर्धारण करना आवश्यक होता है। मौजूदा स्थिति का विश्लेषण करते हुए, प्रत्येक कार्य को स्टीरियोमेट्री के चार मुख्य वर्गों से जोड़ा जा सकता है।

प्रथम श्रेणी में ऐसे कार्य शामिल हैं जिनमें एक सीधी रेखा और एक विमान के बीच समानता को निर्धारित करना आवश्यक है। इसका समाधान उसी नाम के प्रमेय की उपपत्ति के लिए कम हो जाता है। ऐसा करने के लिए, आपको यह निर्धारित करने की आवश्यकता है कि क्या उस रेखा के लिए जो विचाराधीन विमान से संबंधित नहीं है, इस विमान में एक समानांतर रेखा पड़ी है।

दूसरी श्रेणी की समस्याओं में वे शामिल हैं जिनमें समानांतर विमानों के चिह्न का उपयोग किया जाता है। इसका उपयोग प्रूफ प्रक्रिया को सरल बनाने के लिए किया जाता है, जिससे समाधान खोजने में लगने वाला समय काफी कम हो जाता है।

अगली कक्षा में समतलों की समानता के मुख्य गुणों के साथ रेखाओं की संगति पर समस्याओं के स्पेक्ट्रम को शामिल किया गया है। चतुर्थ श्रेणी की समस्याओं का समाधान यह निर्धारित करना है कि समानांतर विमानों की स्थिति पूरी होती है या नहीं। यह जानने के बाद कि किसी विशेष समस्या का प्रमाण कैसे होता है, ज्यामितीय स्वयंसिद्धों के मौजूदा शस्त्रागार को लागू करते समय छात्रों के लिए नेविगेट करना आसान हो जाता है।

इस प्रकार, कार्य, जिसकी स्थिति में सीधी रेखाओं, एक सीधी रेखा और एक दूसरे के साथ एक समतल या दो विमानों की समानता को निर्धारित करने और सिद्ध करने की आवश्यकता होती है, को प्रमेय के सही चयन और समाधान के मौजूदा सेट के अनुसार घटाया जाता है। नियम।

एक सीधी रेखा और एक समतल की समानता पर

एक सीधी रेखा और एक विमान की समानता रूढ़िवादिता में एक विशेष विषय है, क्योंकि यह ठीक यही मूल अवधारणा है जिस पर ज्यामितीय आकृतियों के समानता के बाद के सभी गुण आधारित हैं।

उपलब्ध स्वयंसिद्धों के अनुसार, जब एक सीधी रेखा के दो बिंदु एक निश्चित तल से संबंधित होते हैं, तो हम यह निष्कर्ष निकाल सकते हैं कि दी गई सीधी रेखा भी इसमें निहित है। इस स्थिति में, यह स्पष्ट हो जाता है कि अंतरिक्ष में विमान के सापेक्ष रेखा के स्थान के लिए तीन विकल्प हैं:

1. रेखा विमान से संबंधित है।
2. एक रेखा और एक समतल के लिए प्रतिच्छेदन का एक सामान्य बिंदु होता है।
3. एक सीधी रेखा और एक समतल के लिए कोई प्रतिच्छेदन बिंदु नहीं हैं।

हम विशेष रूप से अंतिम संस्करण में रुचि रखते हैं, जब कोई चौराहे बिंदु नहीं होते हैं। तभी हम कह सकते हैं कि रेखा और तल एक दूसरे के सापेक्ष समानांतर हैं। इस प्रकार, एक सीधी रेखा और एक विमान के समानता के संकेत पर मुख्य प्रमेय की स्थिति की पुष्टि की जाती है, जिसमें कहा गया है कि: "यदि प्रश्न में विमान से संबंधित रेखा उस विमान में किसी भी रेखा के समानांतर नहीं है, तो प्रश्न में रेखा भी दिए गए विमान के समानांतर है।"

समानता के चिह्न का उपयोग करने की आवश्यकता

समतलों के समांतरता चिह्न का प्रयोग सामान्यतः तलों के बारे में समस्याओं का सरलीकृत समाधान खोजने के लिए किया जाता है। इस चिन्ह का सार इस प्रकार है: यदि एक ही तल में दो प्रतिच्छेदी रेखाएँ पड़ी हों, जो किसी दूसरे तल की दो रेखाओं के समानांतर हों, तो ऐसे तलों को समांतर कहा जा सकता है».

अतिरिक्त प्रमेय

एक सुविधा का उपयोग करने के अलावा जो विमानों की समानता को साबित करता है, व्यवहार में दो अन्य अतिरिक्त प्रमेयों के उपयोग का सामना कर सकता है। पहले निम्नलिखित रूप में प्रस्तुत किया गया है: यदि दो समानांतर विमानों में से एक तीसरे के समानांतर है, तो दूसरा विमान या तो तीसरे के समानांतर है, या इसके साथ पूरी तरह से मेल खाता है।».

दिए गए प्रमेयों के उपयोग के आधार पर, विचाराधीन स्थान के संबंध में समतलों की समानता को सिद्ध करना हमेशा संभव होता है। दूसरा प्रमेय एक लंब रेखा पर विमानों की निर्भरता को प्रदर्शित करता है और इसका रूप है: " यदि दो गैर-संपाती तल किसी सीधी रेखा के लंबवत हैं, तो उन्हें एक दूसरे के समानांतर माना जाता है».

एक आवश्यक और पर्याप्त स्थिति की अवधारणा

समतलों की समानता सिद्ध करने की समस्याओं को बार-बार हल करते समय, समतलों की समानता के लिए एक आवश्यक और पर्याप्त स्थिति प्राप्त हुई। यह ज्ञात है कि किसी भी विमान को फॉर्म के पैरामीट्रिक समीकरण द्वारा दिया जाता है: ए 1 एक्स + बी 1 वाई + सी 1 जेड + डी 1 = 0। हमारी स्थिति समीकरणों की एक प्रणाली के उपयोग पर आधारित है जो अंतरिक्ष में विमानों के स्थान को निर्दिष्ट करती है, और निम्नलिखित फॉर्मूलेशन द्वारा इसका प्रतिनिधित्व किया जाता है: दो समतलों की समानता को सिद्ध करने के लिए यह आवश्यक और पर्याप्त है कि इन समतलों का वर्णन करने वाले समीकरणों की प्रणाली असंगत हो, अर्थात इसका कोई हल न हो।».

मूल गुण

हालाँकि, ज्यामितीय समस्याओं को हल करते समय, समानता के चिह्न का उपयोग करना हमेशा पर्याप्त नहीं होता है। कभी-कभी ऐसी स्थिति उत्पन्न हो जाती है जब विभिन्न तलों में दो या दो से अधिक रेखाओं की समांतरता या इन रेखाओं में निहित खंडों की समानता को सिद्ध करना आवश्यक हो जाता है। ऐसा करने के लिए, समांतर विमानों के गुणों का उपयोग करें। ज्यामिति में उनमें से केवल दो हैं।

पहली संपत्ति आपको कुछ विमानों में रेखाओं की समानता का न्याय करने की अनुमति देती है और इसे निम्न रूप में प्रस्तुत किया जाता है: यदि दो समांतर तलों को एक तिहाई द्वारा प्रतिच्छेद किया जाता है, तो प्रतिच्छेदन रेखाओं से बनी रेखाएँ भी एक दूसरे के समांतर होंगी».

द्वितीय गुण का अर्थ समांतर रेखाओं पर स्थित खण्डों की समानता सिद्ध करना है। इसकी व्याख्या नीचे प्रस्तुत की गई है। " यदि हम दो समानांतर तलों पर विचार करें और उनके बीच एक क्षेत्र को घेर लें, तो यह तर्क दिया जा सकता है कि इस क्षेत्र द्वारा बनाए गए खंडों की लंबाई समान होगी».