Navedite primjere koje se ravnine nazivaju paralelnima. Paralelnost ravnina: znak, uvjet. Paralelne ravnine na primjerima

Položaj ravnine u prostoru određen je:

• tri točke koje ne leže na jednoj ravnoj liniji;
• pravac i točka uzeta izvan pravca;
• dvije linije koje se sijeku;
• dvije paralelne crte;
• ravna figura.

U skladu s tim, ravnina se može postaviti na dijagram:

• projekcije tri točke koje ne leže na jednoj ravnoj liniji (Slika 3.1, a);
• projekcije točke i ravne linije (Slika 3.1, b);
• projekcije dviju linija koje se presijecaju (Slika 3.1, c);
• projekcije dviju paralelnih linija (Slika 3.1, d);
• ravna figura (slika 3.1, e);
• tragovi aviona;
• linija najvećeg nagiba ravnine.

Slika 3.1 - Metode zadavanja ravnina

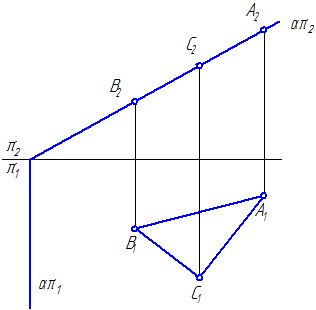
Avion u općem položaju je ravnina koja nije ni paralelna ni okomita ni na jednu od ravnina projekcije.

Prateći avion naziva se ravna crta dobivena kao rezultat presjeka dane ravnine s jednom od ravnina projekcije.

Generička ravnina može imati tri traga: horizontalna – απ 1, frontalni – απ 2 i profil – απ 3 , koju tvori križanjem s poznatim ravninama projekcija: horizontalnom π 1 , frontalnom π 2 i profilnom π 3 (slika 3.2).

Slika 3.2 - Tragovi ravnine općeg položaja

3.2. Privatni položaj aviona

Privatni položaj aviona- ravnina okomita ili paralelna s ravninom projekcija.

Ravnina okomita na ravninu projiciranja naziva se ravnina projiciranja, a na tu ravninu projiciranja projicirat će se u obliku pravca.

Svojstvo ravnine projekcije: sve točke, pravci, ravni likovi koji pripadaju projicirajućoj ravnini imaju projekcije na kosi trag ravnine(Slika 3.3).

Slika 3.3 - Ravnina frontalne projekcije kojoj pripadaju: točke ALI, NA, IZ; linije AC, AB, Sunce; ravnina trokuta ABC

Ravnina frontalne projekcije – ravnina okomita na ravninu frontalne projekcije(Slika 3.4, a).

Horizontalna projekcijska ravnina – ravnina okomita na ravninu horizontalne projekcije(Slika 3.4, b).

Ravnina za projiciranje profila – ravnina okomita na profilnu ravninu projekcija.

Ravnine paralelne s ravninama projekcije nazivaju se ravni ravnine ili dvostruko projicirane ravnine.

Frontalna ravnina – ravnina paralelna s ravninom frontalne projekcije(Slika 3.4, c).

Horizontalna ravnina – ravnina paralelna s horizontalnom ravninom projekcije(Slika 3.4, d).

Ravna profilna ravnina – ravnina paralelna s ravninom projekcije profila(Slika 3.4, e).

Slika 3.4 - Crteži ravnina određenog položaja

3.3. Točka i pravac u ravnini. Pripadanje točki i ravnoj ravnini

Točka pripada ravnini ako pripada bilo kojem pravcu koji leži u toj ravnini(Slika 3.5).

Pravac pripada ravnini ako ima najmanje dvije zajedničke točke s ravninom.(Slika 3.6).

Slika 3.5 - Pripadanje točki u ravnini

α = m // n

D∈ n⇒ D∈ α

Slika 3.6 - Pripadanje ravnoj ravnini

Vježba

Dana je ravnina definirana četverokutom (slika 3.7, a). Potrebno je dovršiti horizontalnu projekciju vrha IZ.

a	b

Slika 3.7 - Rješenje problema

Riješenje :

1. ABCD je ravni četverokut koji određuje ravninu.
2. Nacrtajmo dijagonale u njemu AC i BD(Slika 3.7, b), koje su linije koje se sijeku, a također definiraju istu ravninu.
3. Prema kriteriju sjecišta linija, konstruiramo horizontalnu projekciju točke sjecišta tih linija - K prema poznatoj frontalnoj projekciji: A 2 C 2 ∩ B 2 D 2 =K 2 .
4. Vratite liniju spoja projekcije u sjecište s vodoravnom projekcijom pravca BD: na dijagonalnoj projekciji B 1 D 1 zgrada Do 1 .
5. Kroz ALI 1 Do 1 izvodimo projekciju dijagonale ALI 1 IZ 1 .
6. točka IZ 1 dobivamo pomoću projekcijskog spojnog pravca dok se ne siječe s horizontalnom projekcijom produžene dijagonale ALI 1 Do 1 .

3.4. Glavne linije aviona

U ravnini se može konstruirati beskonačno mnogo pravaca, ali u ravnini leže posebni pravci tzv. glavne linije ravnine (Slika 3.8 - 3.11).

Ravna razina ili ravnina paralelna naziva se pravac koji leži u zadanoj ravnini i paralelan je s jednom od ravnina projekcije.

Horizontalno ili horizontalna linija razine h(prva paralela) je pravac koji leži u zadanoj ravnini i paralelan je s vodoravnom ravninom projekcija (π 1)(Slika 3.8, a; 3.9).

Frontalni ili prednja ravna razina f(druga paralela) je pravac koji leži u zadanoj ravnini i paralelan je s frontalnom ravninom projekcija (π 2)(Slika 3.8, b; 3.10).

Linija profila razine str(treća paralela) je pravac koji leži u zadanoj ravnini i paralelan je s profilnom ravninom projekcija (π 3)(Slika 3.8, c; 3.11).

Slika 3.8 a - Horizontalna ravna crta libele u ravnini zadanoj trokutom

Slika 3.8 b - Frontalna linija nibele u ravnini zadanoj trokutom

Slika 3.8 c - Ravna linija profila u ravnini određenoj trokutom

Slika 3.9 - Horizontalna ravna crta libele u ravnini određenoj tragovima

Slika 3.10 - Linija frontalne razine u ravnini određenoj tragovima

Slika 3.11 - Ravna linija profila u ravnini određenoj tragovima

3.5. Međusobni položaj pravca i ravnine

Pravac u odnosu na zadanu ravninu može biti paralelan i može s njom imati zajedničku točku, odnosno sijeći se.

3.5.1. Paralelnost ravne ravnine

Znak paralelnosti ravne ravnine: pravac je paralelan s ravninom ako je paralelan s bilo kojim pravcem u toj ravnini(Slika 3.12).

Slika 3.12 - Paralelnost ravne ravnine

3.5.2. Presjek pravca s ravninom

Za konstruiranje točke presjeka prave linije s ravninom općeg položaja (slika 3.13) potrebno je:

1. Zaključite ravnu liniju a u pomoćnu ravninu β (kao pomoćnu ravninu treba izabrati ravnine parcijalnog položaja);
2. Odredi presječnu liniju pomoćne ravnine β sa zadanom ravninom α;
3. Pronađite točku sjecišta zadanog pravca a s linijom presjeka ravnina MN.

Slika 3.13 - Konstrukcija točke susreta pravca s ravninom

Vježba

Dano: izravno AB u općem položaju ravnina σ⊥π 1 . (Slika 3.14). Konstruirajte točku sjecišta pravca AB s ravninom σ.

Riješenje :

1. Ravnina σ se horizontalno projicira, dakle, horizontalna projekcija ravnine σ je pravac σ 1 (horizontalni trag ravnine);
2. Točka Do mora pripadati liniji AB ⇒ Do 1 ∈ALI 1 NA 1 i zadane ravnine σ ⇒ Do 1 ∈σ 1 , dakle, Do 1 je u točki sjecišta projekcija ALI 1 NA 1 i σ 1;
3. Točka frontalne projekcije Do nalazimo pomoću linije spajanja projekcije: Do 2 ∈ALI 2 NA 2 .

Slika 3.14 - Presjek pravca općeg položaja s ravninom posebnog položaja

Vježba

Zadano je: ravnina σ = Δ ABC– opći položaj, ravno EF(Slika 3.15).

Potrebno je konstruirati točku sjecišta pravca EF s ravninom σ.

a	b

Slika 3.15 - Sjecište pravca s ravninom

1. Zaključimo ravnu liniju EF u pomoćnu ravninu, za koju ćemo koristiti vodoravno projicirajuću ravninu α (Slika 3.15, a);
2. Ako je α⊥π 1 , tada se na ravninu projekcija π 1 ravnina α projicira u ravnu liniju (vodoravni trag ravnine απ 1 ili α 1) koja se podudara s E 1 F 1 ;
3. Nađimo presječnu liniju (1-2) projicirajuće ravnine α s ravninom σ (razmotrit ćemo rješenje takvog problema);
4. Pravac (1-2) i zadani pravac EF leže u istoj ravnini α i sijeku se u točki K.

Algoritam za rješavanje problema (Slika 3.15, b):

Kroz EF nacrtati pomoćnu ravninu α:

3.6. Određivanje vidljivosti metodom natjecateljskih točaka

Pri ocjeni položaja ovog pravca potrebno je utvrditi - točka kojeg odsječka pravca je bliža (dalje) nama, kao promatračima, gledajući u ravninu projekcije π 1 ili π 2 .

Točke koje pripadaju različitim objektima, a na jednoj od projekcijskih ravnina njihove se projekcije poklapaju (odnosno, dvije točke se projiciraju u jednu), nazivamo konkurentnim na tu projekcijsku ravninu..

Potrebno je posebno definirati vidljivost na svakoj ravnini projekcije.

Vidljivost na π 2 (Sl. 3.15)

Biramo točke koje se natječu na π 2 - točke 3 i 4. Neka je točka 3∈ prije Krista∈σ, točka 4∈ EF.

Za određivanje vidljivosti točaka na ravnini projekcije π 2 potrebno je odrediti položaj tih točaka na horizontalnoj ravnini projekcije gledajući na π 2 .

Smjer gledanja na π 2 prikazan je strelicom.

Iz horizontalnih projekcija točaka 3 i 4, gledajući π 2 , vidljivo je da se točka 4 1 nalazi bliže promatraču nego 3 1 .

4 1 ∈E 1 F 1 ⇒ 4∈EF⇒ točka 4 bit će vidljiva na π 2, koja leži na liniji EF, dakle ravna crta EF na mjestu razmatranih konkurentskih točaka nalazi se ispred ravnine σ i bit će vidljiv do točke K

Vidljivost na π 1

Za određivanje vidljivosti biramo točke koje se natječu na π 1 - točke 2 i 5.

Za određivanje vidljivosti točaka na ravnini projekcije π 1 potrebno je odrediti položaj tih točaka na ravnini frontalne projekcije gledajući u π 1 .

Smjer gledanja na π 1 prikazan je strelicom.

Iz frontalnih projekcija točaka 2 i 5, gledajući π 1 , vidljivo je da se točka 2 2 nalazi bliže promatraču nego 5 2 .

2 1 ∈ALI 2 NA 2 ⇒ 2∈AB⇒ točka 2 bit će vidljiva na π 1, koja leži na liniji AB, dakle ravna crta EF na presjeku razmatranih konkurentskih točaka nalazi se ispod ravnine σ i bit će nevidljiv do točke K su točke presjeka pravca s ravninom σ.

Vidljiva od dvije konkurentne točke bit će ona s većom koordinatom "Z" ili (i) "Y".

3.7. Okomitost ravne ravnine

Znak okomitosti ravne ravnine: Pravac je okomit na ravninu ako je okomit na dva pravca koji se sijeku i leže u zadanoj ravnini.

a	b

Slika 3.16 - Postavljanje pravca okomitog na ravninu

Teorema. Ako je pravac okomit na ravninu, tada je na dijagramu: horizontalna projekcija pravca okomita na horizontalnu projekciju ravnine horizontale, a frontalna projekcija pravca okomita je na frontalnu projekciju frontala. (Slika 3.16, b)

Teorem se dokazuje kroz teorem o pravokutnoj projekciji u konkretnom slučaju.

Ako je ravnina dana tragovima, tada su projekcije ravne linije okomite na ravninu okomite na odgovarajuće tragove ravnine (slika 3.16, a).

Neka linija str okomito na ravninu σ=Δ ABC i prolazi kroz točku K.

1. Konstruirajmo horizontalu i frontalu u ravnini σ=Δ ABC : A-1∈σ; A-1//π 1 ; C-2∈σ; C-2//π 2 .
2. Vrati iz točke K okomito na zadanu ravninu: p1⊥h1 i p2⊥f2, ili p1⊥απ 1 i p2⊥απ 2

3.8. Međusobni položaj dviju ravnina

3.8.1. Planparalelizam

Dvije ravnine mogu biti paralelne i međusobno se sijeku.

Znak paralelnosti dviju ravnina: Dvije ravnine su međusobno paralelne ako su dvije sjecišne prave jedne ravnine paralelne s dvije sjecišne prave druge ravnine.

Vježba

Zadana je ravnina u općem položaju α=Δ ABC i točka F∉α (slika 3.17).

Kroz točku F nacrtati ravninu β paralelnu s ravninom α.

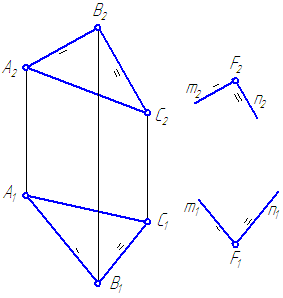
Slika 3.17 - Konstrukcija ravnine paralelne sa zadanom

Riješenje :

Kao presječne pravce ravnine α uzimamo npr. stranice trokuta AB i BC.

1. Kroz točku F nacrtati ravnu liniju m, paralelno, npr. AB.
2. Kroz točku F, ili kroz bilo koju točku koja pripada m, nacrtajte ravnu liniju n, paralelno, npr. Sunce, štoviše m∩n=F.
3. β = m∩n a β//α po definiciji.

3.8.2. Ravno sjecište

Rezultat presjeka 2 ravnine je ravna linija. Bilo koja ravna crta u ravnini ili prostoru može se jednoznačno odrediti s dvije točke. Dakle, da bi se izgradila linija presjeka dviju ravnina, treba pronaći dvije točke zajedničke objema ravninama, a zatim ih spojiti.

Razmotrimo primjere presjeka dviju ravnina s različitim načinima njihovog određivanja: tragovi; tri točke koje ne leže na jednoj ravnoj liniji; paralelne linije; linije koje se sijeku itd.

Vježba

Dvije ravnine α i β zadane su tragovima (slika 3.18). Konstruirajte liniju presjeka ravnina.

Slika 3.18 - Sjecište ravnina u općem položaju, zadano tragovima

Postupak konstruiranja pravca presjeka ravnina:

1. Pronađite točku sjecišta horizontalnih tragova - to je točka M(njezine projekcije M 1 i M 2, dok M 1 =M, jer M - točka posebnog položaja koja pripada ravnini π 1).
2. Pronađite točku sjecišta frontalnih tragova - to je točka N(njezine projekcije N 1 i N 2, dok N 2 = N, jer N- točka posebnog položaja koja pripada ravnini π 2).
3. Konstruirajte crtu presjeka ravnina spajanjem istoimenih projekcija dobivenih točaka: M 1 N 1 i M 2 N 2 .

MN- linija presjeka ravnina.

Vježba

Ravnina σ = Δ ABC, ravnina α se horizontalno projicira (α⊥π 1) ⇒α 1 je horizontalni trag ravnine (slika 3.19).

Konstruirajte presjek tih ravnina.

Riješenje :

Budući da ravnina α siječe stranice AB i AC trokut ABC, zatim sjecišne točke K i L ovih stranica s ravninom α zajedničke su za obje zadane ravnine, što će omogućiti da se njihovim spajanjem pronađe tražena linija presjeka.

Točke se mogu pronaći kao točke sjecišta pravaca s projicirajućom ravninom: pronađite horizontalne projekcije točaka K i L, to je K 1 i L 1 , u sjecištu horizontalnog traga (α 1) zadane ravnine α s horizontalnim projekcijama stranica Δ ABC: ALI 1 NA 1 i A 1 C jedan . Zatim pomoću linija projekcijske veze nalazimo frontalne projekcije tih točaka K2 i L 2 na frontalnim projekcijama ravnih linija AB i AC. Kombinirajmo istoimene projekcije: K 1 i L 1 ; K2 i L 2. Izgrađena je linija presjeka zadanih ravnina.

Algoritam za rješavanje problema:

KL– linija presjeka Δ ABC i σ (α∩σ = KL).

Slika 3.19 - Sjecište ravnina općeg i posebnog položaja

Vježba

Zadane su ravnine α = m//n i ravnina β = Δ ABC(Slika 3.20).

Konstruirajte presjek zadanih ravnina.

Riješenje :

1. Za pronalaženje točaka koje su zajedničke objema zadanim ravninama i koje određuju sjecište ravnina α i β, potrebno je koristiti pomoćne ravnine određenog položaja.
2. Kao takve ravnine biramo dvije pomoćne ravnine određenog položaja, npr.: σ // τ; σ⊥π 2 ; τ⊥π 2 .
3. Novouvedene ravnine sijeku se sa svakom od zadanih ravnina α i β duž ravnih linija koje su međusobno paralelne, budući da je σ // τ:

- rezultat presjeka ravnina α, σ i τ su prave (4-5) i (6-7);

- rezultat presjeka ravnina β, σ i τ su pravci (3-2) i (1-8).

1. Pravci (4-5) i (3-2) leže u ravnini σ; točka sjecišta M istovremeno leži u ravninama α i β, odnosno na presjecištu tih ravnina;
2. Slično, nalazimo točku N, zajednički za ravnine α i β.
3. Spajanjem točaka M i N, konstruiramo presječnu liniju ravnina α i β.

Slika 3.20 - Presjek dviju ravnina u općem položaju (opći slučaj)

Algoritam za rješavanje problema:

Vježba

Ravnine α = Δ ABC i β = a//b. Konstruirajte presječnu liniju zadanih ravnina (slika 3.21).

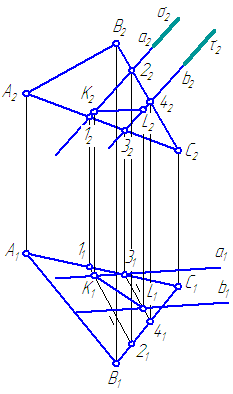
Slika 3.21 Rješavanje zadatka za presjek ravnina

Riješenje :

Upotrijebimo pomoćne sekantne ravnine privatnog položaja. Uvodimo ih na način da smanjimo broj konstrukcija. Na primjer, uvedimo ravninu σ⊥π 2 koja zatvara pravac a u pomoćnu ravninu σ (σ∈ a). Ravnina σ siječe ravninu α po pravoj liniji (1-2), a σ∩β= a. Stoga (1-2)∩ a=K.

Točka Do pripada objema ravninama α i β.

Otuda i točka K, jedna je od željenih točaka kroz koje prolazi presjek zadanih ravnina α i β.

Da bismo pronašli drugu točku koja pripada presjecištu α i β, zaključimo pravac b u pomoćnu ravninu τ⊥π 2 (τ∈ b).

Spajanjem točaka K i L, dobivamo presječnu liniju ravnina α i β.

3.8.3. Međusobno okomite ravnine

Ravnine su međusobno okomite ako jedna od njih prolazi kroz okomitu na drugu.

Vježba

Zadana je ravnina σ⊥π 2 i pravac u općem položaju – DE(Slika 3.22)

Potreban za izgradnju putem DE ravnina τ⊥σ.

Riješenje .

Povucimo okomicu CD na ravninu σ – C 2 D 2 ⊥σ 2 (na temelju ).

Slika 3.22 - Konstrukcija ravnine okomite na zadanu ravninu

Prema teoremu o pravokutnoj projekciji C 1 D 1 mora biti paralelan s osi projekcije. linije koje se sijeku CD∩DE definiraju ravninu τ. Dakle, τ⊥σ.

Slično razmišljanje, u slučaju ravnine u općem položaju.

Vježba

Ravnina α = Δ ABC i točka K izvan ravnine α.

Potrebno je konstruirati ravninu β⊥α koja prolazi točkom K.

Algoritam rješenja(Slika 3.23):

1. Izgradimo horizontalu h i frontalni f u zadanoj ravnini α = Δ ABC;
2. Kroz točku K nacrtati okomicu b na ravninu α (prema teorem okomice na ravninu: ako je pravac okomit na ravninu, onda su njegove projekcije okomite na kose projekcije horizontale i frontale koje leže u ravnini:b 2⊥f2; b 1⊥h1;
3. Ravninu β postavljamo na bilo koji način, npr. β = a∩b, pa je konstruirana ravnina okomita na zadanu: α⊥β.

Slika 3.23 - Konstrukcija ravnine okomite na zadani Δ ABC

3.9. Zadaci za samostalno rješavanje

1. Ravnina α = m//n(Slika 3.24). Poznato je da K∈α.

Nacrtajte frontalnu projekciju točke Do.

Slika 3.24

2. Konstruirajte tragove pravca zadanog segmentom CB, te odrediti kvadrante kroz koje prolazi (slika 3.25).

Slika 3.25

3. Konstruirajte projekcije kvadrata koji pripada ravnini α⊥π 2 ako je njegova dijagonala MN//π 2 (slika 3.26).

Slika 3.26

4. Konstruiraj pravokutnik ABCD s većom stranom Sunce na ravnoj liniji m, pod uvjetom da je omjer njegovih stranica 2 (slika 3.27).

Slika 3.27

5. Ravnina α= a//b(Slika 3.28). Konstruirajte ravninu β paralelnu s ravninom α i udaljenu od nje 20 mm.

Slika 3.28

6. Ravnina α=∆ ABC i točka D D ravnina β⊥α i β⊥π 1 .

7. Zadana je ravnina α=∆ ABC i točka D izvan aviona. Konstruiraj kroz točku D direktno DE//α i DE//π 1 .

Planparalelizam. Ako su dva pravca jedne ravnine koje se sijeku paralelna s dvama pravcima druge ravnine, tada su te ravnine paralelne.
Dokaz. Neka a i b- podaci o avionu, a 1 i a 2- ravne linije u ravnini a, koji se sijeku u točki A, b 1 i b 2 njima paralelnih pravaca u ravnini b. Pretpostavimo da avioni a i b nisu paralelni, odnosno sijeku se duž neke linije S. Ravno a 1 paralelno s pravcem b 1, pa je paralelna sa samom ravninom b(znak paralelnosti pravca i ravnine). Ravno a 2 paralelno s pravcem b2, pa je paralelna sa samom ravninom. b(znak paralelnosti pravca i ravnine). Ravno S pripada ravnini a, dakle barem jedan od redaka a 1 ili a 2 prelazi granicu S, odnosno s njim ima dodirnu točku. Ali ravno S također pripada ravnini b, što znači da prelazak crte S, ravno a 1 ili a 2 prelazi ravninu b, što ne može biti, budući da je izravan a 1 i a 2 paralelno s ravninom b. Iz ovoga slijedi da su avioni a i b ne sijeku, odnosno paralelni su.

Teorem 1 . Ako se dvije paralelne ravnine sijeku s trećom, tada su sjecišne linije paralelne.
Dokaz. Neka a i b su paralelne ravnine, i g - ravnina koja ih siječe. Avion a sijeku s ravninom g u ravnoj liniji a. Avion b sijeku s ravninom g u ravnoj liniji b. Presječne linije a i b leže u istoj ravnini g i stoga mogu biti ili sijeku ili paralelne linije. Ali, budući da pripadaju dvjema paralelnim ravninama, ne mogu imati zajedničkih točaka. Stoga su paralelni.

Teorem 2. Isječci paralelnih pravaca zatvoreni između dvije paralelne ravnine su jednaki.
Dokaz. Neka a i b su paralelne ravnine, i a i b su paralelne linije koje ih sijeku. Kroz ravne linije a i b potrošit ćemo avion g (Ove linije su paralelne, dakle definirati ravninu, i to samo jednu). Avion a sijeku s ravninom g pravac AB . Avion b sijeku s ravninom g duž pravca SD.Prema prethodnom teoremu pravac S paralelno s ravnom linijom d. Direktno a,b, AB i SD pripadaju ravnini g.Četverokut omeđen ovim pravcima je paralelogram (suprotne stranice su mu paralelne). A budući da je to paralelogram, tada su njegove suprotne strane jednake, odnosno AD \u003d BC

Razmatran je odnos paralelnosti ravnina, njegova svojstva i primjene.

Vizualni prikaz položaja dva

Ravnine daju modeliranje pomoću ravnina površina susjednih zidova, stropa i poda sobe, kreveta na kat, dva pričvršćena lista papira

mađioničari itd. (sl. 242-244).

Iako postoji beskonačno mnogo opcija za relativni položaj raznih ravnina, za čije će se utvrđivanje i karakterizaciju naknadno primijeniti mjerenja kutova i udaljenosti, najprije ćemo se zadržati na onima gdje je klasifikacija (kao i linija s ravninama) temelji se na broju njihovih zajedničkih točaka.

1. Dvije ravnine imaju najmanje tri zajedničke točke koje ne leže na istoj ravnini. Takve ravnine se podudaraju (aksiom S 2 , §7).

2. Zajedničke točke dviju ravnina nalaze se na jednoj ravnoj liniji koja je presjecište tih ravnina (aksiom C 3, § 7). Ove se ravnine sijeku.

3. Dvije ravnine nemaju zajedničkih točaka.

NA u ovom slučaju se zovu paralelno-

Dvije ravnine nazivamo paralelnim ako nemaju zajedničkih točaka.

Paralelnost ravnina označava se sa ||: α || β.

Kao i uvijek, pri uvođenju geometrijskih pojmova,

Postoji problem njihove egzistencije. Postojanje unakrsnog

ravnina je karakteristično obilježje prostora,

a koristili smo ga već mnogo puta. Manje očito

postojanje paralelnih ravnina. Ne postoji

sumnje da npr. ravnine suprotnih lica

kocke su joj paralelne, odnosno ne sijeku se. Ali odmah

Naravno, po definiciji, to je nemoguće utvrditi. Za rješavanje

postavljeno pitanje, kao i druga pitanja vezana uz

paralelnost ravnina, potrebno je imati znak paralelnosti.

Za traženje znaka, preporučljivo je uzeti u obzir avion,

"satkana" od ravnih linija. Očito, svaki redak jednog od

paralelne ravnine moraju biti paralelne jedna s drugom.

Inače će ravnine imati zajedničku točku. dosta-

Jesu li paralelnosti ravnine β točno s jednom ravnom ravninom α

tako da su ravnine α i β paralelne? Bezuvjetno

ali, ne (opravdajte!). Praktična iskustva to pokazuju

dovoljne su dvije takve crte koje se sijeku. Zakačiti

na jarbol platforma paralelna s tlom, dovoljno ju je staviti

paralelne s drugom ravninom, tada su te ravnine paralelne.

 Neka su presječne prave a i b ravnine α paralelne s ravninom β. Dokažimo suprotno da su ravnine α i β paralelne. Za to pretpostavimo da se ravnine α i β sijeku po pravoj liniji

t (slika 246). Pravci a i b ne mogu sijeći pravac m prema pretpostavci. Međutim, tada su u ravnini α kroz jednu točku povučene dvije prave koje se ne sijeku s pravcem m, odnosno paralelne su s njim. To je kontradikcija

i dovršava dokaz teorema.

Oznaka paralelnosti ravnina koristi se za horizontalno postavljanje ravnih konstrukcija (betonskih ploča, podova, diskastih goniometara itd.) pomoću dvije razine postavljene u ravnini konstrukcije na presječne linije. Na temelju ove značajke možete izgraditi ravninu paralelnu sa zadanom.

Zadatak 1. Kroz točku koja leži izvan zadane ravnine povuci ravninu paralelnu sa zadanom.

 Neka su ravnina β i točka M zadane izvan ravnine (slika 247, a). Povuci kroz točku M dva pravca a i b koji se sijeku, paralelna s ravninom β. Da biste to učinili, trebate uzeti u ravninu β dvije crte c i d koje se sijeku (slika 247, b). Zatim kroz točku M povucite pravce a i b paralelne s pravcima c odnosno d.

ali (Slika 247, c).

Sjecište pravaca a i b paralelne su s ravninom β, prema kriteriju paralelnosti pravca i ravnine (teorem 1 §11). Oni jednoznačno određuju ravninu α. Prema dokazanom kriteriju, α || β.

Primjer 1. Dana je kocka ABCDA 1 B 1 C 1 D 1, točke M, N, P su polovišta bridova BC, redom B 1 C 1, A 1 D 1. Postavite relativni položaj ravnina: 1) ABB 1 i PNM; 2) NMA i A1C1C; 3) A 1 NM

i PC 1 C; 4) MAD 1 i DB 1 C.

 1) Ravnine ABB 1 i RNM (sl. 248) su paralelne, na temelju paralelnosti ravnina (teorem 1). Doista, pravci PN i NM sijeku se i paralelni su s ravninom ABB 1, prema znaku paralelnosti pravca i ravnine (teorem 1 iz §11), jer odsječci PN i NM spajaju središta suprotnih stranica ravnine. kvadrata, dakle paralelni su sa stranicama kvadrata:

PN || A 1 B 1 , NM || U 1 B.

2) Ravnine NMA i A 1 C 1 C sijeku se po pravcu AA 1 (sl. 249). Doista, pravci AA 1 i CC 1 su paralelni, prema znaku paralelnosti (AA 1 || BB 1 , BB 1 || CC 1 ). Dakle, pravac AA 1 leži u ravnini A 1 C 1 C . Na sličan se način opravdava pripadnost pravca AA 1 ravnini NMA.

3) Ravnine A 1 NM i PC 1 C (sl. 250) su paralelne, na temelju paralelnosti ravnina. Doista, NM || Sa 1 C. Dakle, pravac NM je paralelan s ravninom PC 1 C. Odsječci PC 1 i A 1 N također su paralelni jer je četverokut PC 1 NA 1 paralelogram (A 1 P || NC 1 , A 1 P = NC 1). Dakle, pravac A 1 N paralelan je s ravninom PC 1 C. Pravci A 1 N i NM se sijeku.

4) Ravnine MAD 1 i DB 1 C se sijeku (slika 251). Iako nije lako povući crtu njihova sjecišta, nije teško naznačiti jednu točku te linije. Doista, pravci A 1 D i B 1 C su paralelni, jer je četverokut A 1 B 1 CD paralelogram (A 1 B 1 \u003d AB \u003d CD, A 1 B 1 || AB, AB || CD) . Dakle, pravac A 1 D pripada ravnini DB 1 C. Pravci A 1 D i AD 1 sijeku se u zajedničkoj točki ravninama MAD 1 i DB 1 C.

Ako su dva pravca jedne ravnine koji se sijeku paralelna s dvama pravcima druge ravnine, tada su te ravnine paralelne.

Korištenjem znaka paralelnosti pravca i ravnine (teorem 1 §11) lako je utvrditi da uvjet teorema 1 slijedi iz uvjeta teorema 1′.′.

Naravno, postavlja se pitanje jedinstvenosti konstrukcije dane u problemu 1. Budući da ćemo ovo svojstvo morati koristiti više puta, izdvajamo ga kao poseban teorem. Prvo, međutim, razmotrite još jednu izjavu.

Teorem 2 (o presjeku dviju paralelnih ravnina trećom).

Ako su dvije paralelne ravnine presječene trećom ravninom, tada su sjecišne linije ravnina paralelne.

 Neka su zadane paralelne ravnine α, β i ravnina γ koja ih siječe (slika 252). Označite linije sjecišta

kroz a i b. Ovi pravci leže u ravnini γ i ne sijeku se jer ravnine α i β nemaju zajedničkih točaka. Stoga, izravni

moji a i b su paralelni.

Teorem 3 (o postojanju i jedinstvenosti ravnine paralelne s danom).

Kroz točku izvan zadane ravnine prolazi samo jedna ravnina paralelna zadanoj ravnini.

 Konstrukcija takve ravnine izvedena je u zadatku 1. Jedinstvenost konstrukcije ćemo dokazati kontradikcijom. Pretpostavimo da su kroz točku M povučene dvije različite ravnine α i γ, pa-

paralelne ravnine β (sl. 253), a pravac m je pravac njihova sjecišta. Povucimo kroz točku M ravninu δ koja se siječe s pravcem

m i ravnina β (kako se to može učiniti?). Označimo s a i b

presječna linija ravnine δ s ravninama α i γ, a kroz c - presječna linija ravnina δ i β (slika 253). Prema teoremu 2, i || S

i b || S. To jest, u δ ravnini kroz

točkom M prolaze dva pravca paralelna s pravcem c. Kontradikcija ukazuje na netočnost pretpostavke.

Odnos paralelnosti ravnina ima niz svojstava koja imaju analogije u planimetriji.

Teorem 4 (o odsječcima paralelnih pravaca između paralelnih ravnina).

Segmenti paralelnih pravaca odsječeni paralelnim ravninama međusobno su jednaki.

 Neka su dvije paralelne ravnine α i β i odsječci AB

a CD paralelne linije a i d, odsječene ovim ravninama (slika 254, a). Nacrtajmo ravninu γ kroz pravce a i d (slika 254, b). On siječe ravnine α i β duž pravaca AC i BD koji su prema teoremu 2 paralelni. Dakle, četverokut ABCD je paralelogram, njegove suprotne stranice AC i BD su jednake.

Iz gornjeg svojstva proizlazi da ako oduzmemo od svih točaka ravnine

paralelnih odsječaka iste duljine na jednoj strani ravnine, tada krajevi tih odsječaka tvore dvije paralelne ravnine. Na tom se svojstvu temelji konstrukcija paralelopipeda slaganjem segmenata (slika 255).

Teorem 5 (o tranzitivnosti relacije paralelnosti ravnina).

Ako je svaka od dvije ravnine paralelna s trećom, tada su te dvije ravnine međusobno paralelne.

 Neka su ravnine α i β paralelne s ravninom γ. Pretpostavimo da

α i β nisu paralelni. Tada ravnine α i β imaju zajedničku točku, a kroz tu točku prolaze dvije različite ravnine koje su paralelne s ravninom γ, što je u suprotnosti s teoremom 3. Dakle, ravnine α i β nemaju zajedničkih točaka, tj. paralelno.

Teorem 5 je još jedan znak paralelnosti ravnina. Široko se koristi u geometriji iu praktičnim aktivnostima. Na primjer, u višekatnoj zgradi, paralelizam ravnina poda i stropa na svakom katu jamči njihovu paralelnost na različitim katovima.

Zadatak 2. Dokažite da ako pravac a siječe ravninu α, onda siječe i svaku ravninu paralelnu s ravninom α.

 Neka su ravnine α i β paralelne, a pravac a siječe ravninu α u točki A. Dokažimo da i ona siječe ravninu

β. Pretpostavimo da to nije slučaj. Tada je pravac a paralelan s ravninom β. Povucimo ravninu γ kroz pravac a i proizvoljnu točku ravnine β (slika 256).

Ta ravnina siječe paralelne ravnine α i β po ravnima b i c. su-

prema teoremu 2, b || c, odnosno u ravnini γ kroz točku A prolaze dvije prave a i b paralelne s pravcem c . Ova kontradikcija dokazuje tvrdnju.

Pokušajte sami dokazati da ako ravnina α siječe ravninu β, onda siječe i svaku ravninu paralelnu s ravninom β.

Primjer 2. U tetraedru ABCD točke K, F, E su polovišta bridova DA, DC, DB, a M i P su središta mase stranica ABD, odnosno BCD.

1) Postavite međusobni položaj ravnina KEF i ABC;

DEF i ABC.

2) Konstruirajte presječnu liniju ravnina AFB i KEC.

3) Odredite površinu presjeka tetraedra ravninom koja je paralelna s ravninom ABD i prolazi kroz točku P, ako su svi rubovi tetraedra jednaki a.

 Izgradimo sliku koja odgovara stanju (Sl. 257, a). 1) Ravnine KEF i ABC su paralelne, na temelju paralelnosti ravnina (teorem 1'): sjecišne pravce KE i KF ravnine KEF paralelne su s presječnim pravcima AB i AC ravnine ABC (tj. središnje linije odgovarajućih

crtanje trokuta).

Ravnine DEF i ABC sijeku se duž pravca BC jer pravac BC pripada objema ravninama i ne mogu se poklapati - točke A, B, C, D ne leže u istoj ravnini.

2) Ravnina AFB siječe se s ravninom KEC duž pravca koji sadrži točku P, jer su pravci CE i BF koji leže u tim ravninama u ravnini BCD i sijeku se u točki P. Druga točka je sjecište Q linija AF i CK u ravnini ACD (slika 257, b). Očito, ova točka je središte mase lica ACD. Željeno sjecište je pravac PQ.

3) Izgradimo presjek naveden u uvjetu, koristeći znak paralelnosti ravnina. Povucimo linije kroz točke P i Q paralelne s linijama DB i DA (slika 257, c). Ove linije sijeku segment CD u točki L. Potonje proizlazi iz svojstva središta mase trokuta - ono dijeli medijane trokuta u omjeru 2:1, računajući od vrha. Ostaje primijeniti Thalesov teorem. Dakle, ravnine PLQ i BDA su paralelne. Traženi presjek je trokut LSN.

Po konstrukciji su trokuti BCD i SCL slični s koeficijentom sličnosti CE CP = 3 2 . Stoga je LS = 3 2 BD . Slično tome,

zbrajaju se jednakosti: LN = 3 2 AD , NS = 3 2 AB . To implicira da su trokuti LSN i ABD slični s koeficijentom sličnosti 3 2 . Po svojstvima površina sličnih trokuta,

S LNS = 4 9 S ABD . Ostaje pronaći površinu trokuta ABD. Po-

budući da su, prema pretpostavci, svi bridovi tetraedra jednaki a, tada je S ABD = 4 3 a 2 .

Željena površina je 3 1 3 a 2 .

Prikladno je obratiti pozornost na činjenicu da odgovor ovisi samo o području aspekta ABD. Stoga je jednakost svih rubova samo sredstvo da se pronađe ovo područje. Stoga se ovaj problem može bitno generalizirati.

Odgovor. 1) KEF || ABC; 3) 3 1 3 a 2 .

 Kontrolna pitanja

1. Je li točno da su dvije ravnine paralelne ako je svaki pravac u jednoj ravnini paralelan s drugom ravninom?

2. Ravnine α i β su paralelne. Leže li u tim ravninama pravci koji se sijeku?

3. Dvije stranice trokuta paralelne su s nekom ravninom. Je li treća stranica trokuta paralelna s tom ravninom?

4. Dvije stranice paralelograma paralelne su s nekom ravninom. Je li točno da je ravnina paralelograma paralelna sa zadanom ravninom?

5. Mogu li odsječci dviju ravnina odsječenih paralelnim ravninama biti nejednaki?

6. Može li presjek kocke biti jednakokračni trapez? Može li presjek kocke biti pravilan peterokut? Je li točno da su dvije ravnine paralelne s istim pravcem međusobno paralelne?

Sjecišta ravnina α i β s ravninom γ međusobno su paralelne. Jesu li ravnine α i β paralelne?

Mogu li tri stranice kocke biti paralelne s istom ravninom?

Grafičke vježbe

1. Slika 258 prikazuje kocku ABCDA 1 B 1 C 1 D 1 , točke M , N , K , L , P su polovišta odgovarajućih bridova. Ispunite tablicu prema zadanom uzorku, odabirući željeni raspored ravnina α i β.

Uzajamno

mjesto

α || β α = β

α × β α || β α = β

2. Na sl. 259 prikazan je tetraedar ABCD, točke K, F, M, N, Q su polovišta odgovarajućih bridova. Navedite:

1) ravnina koja prolazi točkom K paralelno s ravninom ABC;

2) ravnina koja prolazi pravcem BD paralelno s ravninom MNQ.

3. Odredi koliki je presjek lika ravninom koja prolazi kroz zadane tri točke prikazane na slici.

kah 260, a)–e) i 261, a)–d).

4. Napravite crtež prema zadanim podacima.

1) Iz vrhova paralelograma ABCD, koji leže u jednoj od dviju paralelnih ravnina, povučeni su paralelni pravci koji drugu ravninu sijeku redom u točkama A 1 , B 1 , C 1 , D 1 .

2) Trokut A 1 B 1 C 1 je projekcija trokuta ABC na ravninu α koja mu je paralelna. Točka M je sredina BC, M 1 je projekcija točke M na ravninu α.

207. U kocki ABCDA 1 B 1 C 1 D 1 točke O , O 1 su središta stranica ABCD odnosno A 1 B 1 C 1 D 1 , M je polovište brida AB .

1°) Odredi međusobni položaj ravnina MO 1 O

i ADD 1 , ABD 1 i CO 1 C 1 .

2°) Konstruirajte sjecište ravnine DCC 1 i pravca MO 1 i presjecište ravnina MCC 1 i A 1 D 1 C 1 .

3) Odredite površinu presjeka kocke ravninom koja je paralelna s ravninom AD 1 C 1 i prolazi kroz točku O 1 ako je rub kocke a.

208. U tetraedru ABCD točke K , L , P su središta masa redom stranica ABD , BDC , ABC, a M je polovište brida AD .

1°) Odredite međusobni položaj ravnina ACD

i KLP; MLK i ABC.

2°) Konstruirajte sjecište ravnine ABC i pravca ML i presjecište ravnina MKL i ABC.

3) Odredite površinu presjeka tetraedra ravninom koja prolazi kroz točke K, L i M paralelno s pravcem AD, ako su svi rubovi tetraedra jednaki a.

209. Dana je kocka ABCDA 1 B 1 C 1 D 1 . Točke L, M, M 1 polovišta su bridova AB, AD odnosno A 1 D 1.

1°) Odredi međusobni položaj ravnina B 1 D 1 D

i LMM1.

2) Konstruirajte ravninu koja prolazi točkom M paralelno s ravninom ACC 1 .

3) Konstruirajte presjek kocke ravninom koja prolazi točkom M 1 paralelno s ravninom CDD 1 .

4) Odredi međusobni položaj ravnina MA 1 IN 1

i CDM1.

5) Konstruirajte ravninu koja prolazi pravcem C 1 D 1 paralelno s ravninom CDM 1 .

210. U pravilnoj četverokutnoj piramidi SABCD svi bridovi su međusobno jednaki. Točke L, M i N su polovišta bridova AS, BS, CS redom.

1°) Odredi međusobni položaj: pravaca LM i BC ; pravac LN i ravnine ABD; ravnine LMN i BDC .

2°) Dokažite da su trokuti ABC i LMN slični.

3) Konstruirajte presjek piramide ravninom AMN ; ravnina LMN; ravnina LBC.

4*) Koji od presjeka piramide koji prolazi vrhom S ima najveću površinu?

Paralelnost pravaca i ravnina

U SABC tetraedru sva lica su pravilni trokuti. Točke L, M i N su polovišta bridova AS, BS, CS. 1°) Odredi međusobni položaj pravaca LM i BC. 2°) Odredi međusobni položaj pravca LN i ravnine ABC.

3) Dokažite da su trokuti LMN i ABC slični.

Konstruiraj presjek kocke koji je: 1°) jednakostranični trokut; 2) peterokut.

217. Konstruirajte presjek tetraedra koji je paralelogram.

218°. Dokažite da su suprotne plohe paralelopipeda paralelne.

219. Dokaži da skup svih pravaca koji prolaze kroz zadanu točku i paralelni su sa zadanom ravninom čini ravninu paralelnu sa zadanom ravninom.

220. Date su četiri točke A , B , C , D koje ne leže u istoj ravnini. Dokažite da svaka ravnina paralelna s pravcima AB i CD siječe pravce AC, AD, BD, BC u vrhovima paralelograma.

221. Dokaži da su ravnina i pravac koji ne pripada toj ravnini međusobno paralelni ako su oboje paralelni s istom ravninom.

222. Kroz sjecište O dijagonala kocke ABCDA 1 B 1 C 1 D 1 povučena je ravnina paralelna s plohom ABCD. Ova ravnina siječe bridove BB 1 i CC 1 u točkama M odnosno N. Dokažite da je kut MON pravi kut.

223. Dokažite da su dvije ravnine međusobno paralelne ako i samo ako svaki pravac koji siječe jednu od ravnina siječe i drugu.

224*. U trokutastoj piramidi SABC kroz segmente AD i CE, gdje je D sredina SB, a E sredina SA, nacrtajte isječke piramide međusobno paralelne.

225. Pronađite geometrijska mjesta:

1) središta svih segmenata s krajevima na dvije zadane paralelne ravnine; 2*) središta odsječaka s krajevima na dvjema zadanim pravcima koji se sijeku.

226*. Stranica AB trokuta ABC koja leži u ravnini α paralelna je s ravninom β. Jednakostranični trokut A 1 B 1 C 1 je paralelna projekcija trokuta ABC na ravninu β; AB = 5, BC = 6, AC = 9.

1) Postavite relativni položaj pravaca AB i A 1 B 1,

BC i B1 C1 , A1 C1 i AC.

2) Pronađite površinu trokuta A 1 B 1 C 1.

227*. Zadane su dvije crte koje se sijeku. Odredite skup svih točaka u prostoru kroz koje je moguće povući pravac koji siječe svaki od dva zadana pravca.

Osnovna definicija

Dva aviona su tzv

su paralelni,

ako nemaju dodirnih točaka.

Glavne izjave

Znak paralelnosti Ako su dva sjecišta dviju pravaca jedne ravnine ravnine redom paralelna s dvama pravcima druge ravnine, te ravnine

kosti su paralelne.

Teorem o ne- Ako dva paralelna sjecišta dviju paralelnih ravnina sijeku treću ravninu ravninom, tada su pravci trećeg sjecišta ravnine.

to su paralelne.

a α,b α,a ×b ,c β, d β, a || c , b || dα || β

α || β, a = γ∩α, b = γ∩β a || b

Mα

β: α || β, M β

Pripreme za tematski

kome ocjena na temu "Paralelnost pravaca i ravnina"

Zadaci za samokontrolu

1. Četiri točke ne pripadaju istoj ravnini. Mogu li neka tri od njih ležati na istoj liniji?

2. Mogu li tri različite ravnine imati točno dvije zajedničke točke?

3. Mogu li dva pravca koji se sijeku biti istovremeno paralelna s trećim pravcem?

4. Je li istina da ravno a i b nisu paralelni ako ne postoji pravac c paralelan s a i b?

5. Mogu li jednaki segmenti imati nejednake projekcije?

6. Može li zraka biti paralelna projekcija pravca?

7. Može li kvadrat biti slika kocke?

8. Je li točno da kroz danu točku u prostoru može proći samo jedna ravnina paralelna s danim pravcem?

9. Je li uvijek moguće povući pravac kroz zadanu točku paralelan s dvjema zadanim ravninama koje ne sadrže tu točku?

10. Je li moguće povući paralelne ravnine kroz dvije crte koje se sijeku?

Odgovori na zadatke za samokontrolu

Ispitni uzorak

Dva paralelograma ABCD i ABC 1 D 1 leže u različitim ravninama.

1°) Odredi međusobni položaj pravaca CD i C 1 D 1 .

2°) Odredi međusobni položaj pravca C 1 D 1 i ravnine

3°) Konstruirajte presjek ravnina DD 1 C 1 i BCC 1 .

4 °) Odredite međusobni položaj ravnina ADD 1 i BCC 1.

5) Kroz točku M, dijeleći segment AB u omjeru 2:1, računajući od točke A, nacrtajte ravninu α paralelnu s ravninom C 1 BC. 6) Konstruirajte presječnu točku pravca AC s ravninom α i pronađite omjer u kojem ta točka dijeli dužinu AC.

Međusobni raspored pravaca i ravnina u prostoru

Trigonometrijski

Već ste se bavili trigonometrijskim funkcijama na nastavi geometrije. Do sada su njihove primjene uglavnom bile ograničene na rješavanje trokuta, odnosno radilo se o pronalaženju nekih elemenata trokuta iz drugih. Iz povijesti matematike poznato je da je nastanak trigonometrije povezan s mjerenjem duljina i kutova. Međutim, sada opseg

nju primjene su mnogo šire nego u antici.

Riječ "trigonometrija" dolazi od grčke riječi τριγωνον

(trigonon) - trokut i µετρεω (metreo) - mjerim, mijenjam

ryu. Doslovno, to znači mjerenje trokuta.

NA Ovo poglavlje sistematizira gradivo koje vam je već poznato iz kolegija geometrije, nastavlja proučavanje trigonometrijskih funkcija i njihove primjene za karakterizaciju periodičnih procesa, posebno rotacijskog gibanja, oscilatornih procesa itd.

Većina primjena trigonometrije tiče se upravo periodičkih procesa, odnosno procesa koji se ponavljaju u pravilnim intervalima. Izlazak i zalazak Sunca, promjena godišnjih doba, okretanje kotača najjednostavniji su primjeri takvih procesa. Mehaničke i elektromagnetske oscilacije također su važni primjeri periodičnih procesa. Stoga je proučavanje periodičnih procesa važan zadatak. A uloga matematike u njegovom rješavanju je odlučujuća.

priprema za proučavanje teme "Trigonometrijske funkcije"

Preporučljivo je započeti proučavanje teme "Trigonometrijske funkcije" ponavljanjem definicija i svojstava trigonometrijskih funkcija kutova trokuta i njihove primjene za rješavanje pravokutnih i proizvoljnih trokuta.

Sinus, kosinus, tangens, kotangens kutova pravokutnika

trokut

Tablica 24

Sinus oštrog kuta je omjer suprotnog kraka i hipotenuze:

sinα = a c .

Kosinus oštrog kuta je omjer susjedne noge i hipotenuze:

cosα = b c .

Tangens oštrog kuta je omjer suprotnog kraka i susjednog:

tgα = a b .

Kotangens oštrog kuta je omjer susjednog kraka i suprotnog:

ctga = a b .

Sinus, kosinus, tangens, kotangens kutova od 0° do 180°

Tablica 25

sin α = R y ; cosα = R x;

tgα = x y ; ctgα = x g.

(x; na) - koordinate točke ALI nalazi se na gornjem polukrugu, α - kut koji tvori radijus OA krug s osi x.

Vrijednosti sinusa, kosinusa, tangensa, kotangensa

neki kutovi

Tablica 26

Kutak t

Rješavanje proizvoljnih trokuta

Tablica 27

Sinusni teorem

Stranice trokuta proporcionalne su sinusima suprotnih kutova:

grijeh aα = grijeh bβ = grijeh cγ .

Kosinusni teorem

Kvadrat proizvoljne stranice trokuta jednak je zbroju kvadrata druge dvije stranice bez umnožavanja tih stranica s kosinusom kuta između njih:

c2 = a2 + b2 − 2 ab cos γ ,b2 = a2 + c2 − 2 ak cos β , a2 = b2 + c2 − 2 prije Krista cos α .

Površina trokuta je polovica umnoška njegovih dviju stranica i sinusa kuta između njih:

S= 1 2 abgrijehγ = 1 2 akgrijehβ = 1 2 prije Kristagrijehα .

Osnovni trigonometrijski identiteti

5. Usporedite zbroj sinusa šiljastih kutova proizvoljnog pravokutnog trokuta (označavamo ga sALI) s jedinstvom.

< 1. B.ALI= 1.

> 1. G. Nemoguće je usporediti. Poredajte uzlaznim redoslijedom: a= sin 30°, b= cos 30°,

= tg 30°.

< b< c. B.a< c< b. NA.c< a< b. G.b< a< c.

Usporedite bez računalnih sredstava šiljaste kutove α i β, 7.

15. Navedite koordinate točkeALI koji leži na kružnici radijusa 1 (vidi sliku).

(−1; 0). B.(1; 0).

(0; − 1). G.(0; 1).ALI.NA.

Svaka tehnološka operacija može se izvesti s određenom točnošću, što znači da dimenzije dijela dobivenog obradom neće biti idealne, mogu varirati u određenom rasponu. Kako bi se ispunili uvjeti montaže i osigurao pouzdan rad dijela u zadanim uvjetima, potrebno je postaviti dopušteni interval u kojem mora biti konačna veličina. Ovaj interval može regulirati ne samo linearne ili dijametralne dimenzije, već i oblik ili relativni položaj površina.

Tolerancije oblika i položaja dodjeljuje projektant na temelju uvjeta montaže i značajki rada dijela u mehanizmu.

Vrste tolerancija oblika

Tolerancija oblika naziva najveća dopuštena vrijednost odstupanja oblika.

Polje tolerancije oblika- ovo je područje na ravnini ili u prostoru, unutar kojeg se sve točke razmatranog elementa moraju nalaziti unutar normaliziranog područja, čija je širina ili promjer određena vrijednošću tolerancije, a položaj u odnosu na pravi element susjednim elementom.

Odstupanja oblika i tolerancije

Postoje sljedeće tolerancije za odstupanja oblika:

• Odstupanje od ravnosti u ravnini
• konveksan
• konkavnost
• Odstupanje od ravnosti i tolerancija ravnosti
• Konveksan
• Konkavnost
• Odstupanje od zaobljenosti i tolerancija zaobljenosti
• ovalnost
• Izrezati
• Odstupanje cilindričnosti i tolerancija cilindričnosti
• Odstupanje i tolerancija profila uzdužnog presjeka cilindrične površine
• Odstupanje profila uzdužnog presjeka
• sužavanje
• oblik bačve
• oblik sedla

Dopuštena odstupanja označena su posebnim znakovima.

Vrste tolerancija položaja

Tolerancija lokacije- granica koja ograničava dopuštenu vrijednost odstupanja lokacije.

Postoje tolerancije lokacije i tolerancije orijentacije.

Polje tolerancije lokacije- područje na ravnini ili u prostoru, unutar kojega se mora nalaziti susjedni element ili ravnina simetrije, os, središte unutar normaliziranog područja, čiji je promjer ili širina određena tolerancijskom vrijednošću i relativna položaj je određen nominalnim položajem predmetnog elementa.

Odstupanja i tolerancije lokacije

Postoje sljedeće vrste tolerancija lokacije:

• Odstupanje paralelizma i tolerancija paralelizma
• Tolerancija odstupanja i okomitosti
• Tolerancija odstupanja i nagiba
• Tolerancija odstupanja i poravnanja
• Tolerancija radijusa
• Tolerancija odstupanja i simetrije
• Položajna devijacija i položajna tolerancija
• Tolerancija u dijametralnim uvjetima
• Tolerancija radijusa
• Odstupanje od sjecišta i tolerancija sjecišta osi
• Tolerancija u dijametralnim uvjetima
• Tolerancija radijusa

Ukupna dopuštena odstupanja

Postoji nekoliko vrsta ukupnih tolerancija oblika i položaja.

• Radijalno odstupanje
• Potpuno radijalno odstupanje
• Pobjeći u lice
• Potpuno aksijalno odstupanje
• Istrčavanje u zadanom smjeru
• Odstupanje i tolerancija oblika zadanog profila
• Odstupanje i tolerancija oblika zadane površine

Ove su tolerancije označene simbolima.

Označavanje tolerancija oblika i položaja na crtežima

Tolerancije oblika i položaja prikazane su na crtežima u obliku okvira koji je podijeljen na nekoliko dijelova. U prvom dijelu prikazana je grafička oznaka tolerancije, u drugom dijelu - brojčana vrijednost tolerancije, u trećem i sljedećim - slovna oznaka jedne ili više baza.

U nedostatku baze tolerancije, okvir se sastoji od samo dva dijela. Primjeri okvira tolerancije oblika i položaja prikazani su na slici.

Slika lijevo prikazuje okvir s tolerancijom oblika (dopušteno odstupanje od ravnosti), desno s tolerancijom položaja (dopušteno odstupanje od paralelnosti).

Okvir je izrađen tankim linijama. Visina teksta u okviru treba biti jednaka veličini slova dimenzijskih brojeva. Crta koja završava strelicom povlači se od okvira tolerancije do površine ili do vođice.

Ispred brojčane vrijednosti tolerancije mogu se označiti znakovi:

• f - ako je valjkasto ili kružno tolerancijsko polje označeno promjerom
• R - ako je valjkasto ili kružno polje označeno radijusom
• T - ako je tolerancijsko polje za sjecište osi, simetrija, ograničeno na dva paralelna pravca ili ravnine u dijametralnom smislu.
• T / 2 - u istom slučaju kao i T, samo u izrazu radijusa
• Sfera - za sferno tolerancijsko polje.

Ako se tolerancija ne smije primijeniti na cijelu površinu, već samo na određeno područje, tada je označena crticom s točkastom linijom.

Za jedan element može se odrediti više tolerancija, u ovom slučaju okviri se crtaju jedan iznad drugog.

Dodatne informacije mogu se pojaviti iznad ili ispod okvira.

Informacije o tolerancijama oblika i položaja mogu se navesti u .

Neodređene tolerancije poravnanja prema GOST 25069-81.

Zavisna odstupanja

Tolerancije ovisne lokacije označene su sljedećim simbolom.

Ovaj simbol može se staviti iza brojčane vrijednosti tolerancije, ako je zavisna tolerancija povezana sa stvarnim dimenzijama predmetnog elementa. Također, simbol se može postaviti nakon oznake slova (ako ga nema, onda u trećem polju okvira) ako je zavisna tolerancija povezana sa stvarnim dimenzijama osnovnog elementa.

Dodijelite tolerancije oblika i položaja

Što je dio preciznije izrađen, to će biti potrebni precizniji alati za njegovu izradu i kontrolu dimenzija. To će automatski povećati njegovu vrijednost. Ispada da trošak proizvodnje dijela uvelike ovisi o potrebnoj točnosti u njegovoj izradi. To znači da dizajner mora navesti samo one tolerancije koje su stvarno potrebne za montažu i pouzdan rad mehanizma. Dopuštene intervale treba također odrediti na temelju uvjeta sakupljanja i izvedbe.

Brojčane vrijednosti tolerancije oblika

Ovisno o klasi točnosti, postavljaju se standardne vrijednosti tolerancija oblika.

Tolerancije ravnosti i ravnosti

U tom se slučaju nazivna veličina smatra nazivnom duljinom normaliziranog presjeka.

Tolerancije zaobljenosti, cilindričnosti, profila uzdužnog presjeka

Ove tolerancije se dodjeljuju u slučajevima kada moraju biti manje od tolerancije veličine.

Nazivna veličina je nazivni promjer površine.

Tolerancije za okomitost, paralelizam, nagib, aksijalno odstupanje

Nazivna veličina pri dodjeljivanju tolerancija za paralelizam, okomitost, nagib podrazumijeva se kao nazivni normalizirani presjek ili nazivna duljina cijele kontrolirane površine.

Tolerancije radijalnog odstupanja, simetrije, koaksijalnosti sjecišta osi u dijametralnom smislu

Pri dodjeljivanju tolerancija radijalnog odstupanja, nazivna veličina se smatra nazivnim promjerom predmetne površine.

U slučaju zadavanja tolerancija simetrije, sjecišta osi nivelacije, nazivna veličina je nazivni promjer površine ili nazivna veličina između površina koje tvore predmetni element.

Svatko tko je ikada studirao ili trenutno studira u školi morao se suočiti s raznim poteškoćama u proučavanju disciplina koje su uključene u program koji je izradilo Ministarstvo obrazovanja.

S kojim poteškoćama se susrećete

Proučavanje jezika popraćeno je pamćenjem postojećih gramatičkih pravila i glavnih iznimaka od njih. Tjelesni odgoj zahtijeva od učenika veliku računicu, dobru tjelesnu formu i veliko strpljenje.

Međutim, ništa se ne može usporediti s poteškoćama koje se javljaju u proučavanju egzaktnih disciplina. Algebra, koja sadrži zamršene načine rješavanja elementarnih problema. Fizika s bogatim skupom formula za fizičke zakone. Geometrija i njezini dijelovi koji se temelje na složenim teoremima i aksiomima.

Primjer su aksiomi koji objašnjavaju teoriju paralelizma ravnina, koji se moraju zapamtiti, budući da su u osnovi cijelog školskog kurikuluma o stereometriji. Pokušajmo shvatiti kako se to lakše i brže može učiniti.

Paralelne ravnine na primjerima

Aksiom koji ukazuje na paralelnost ravnina je sljedeći: " Bilo koje dvije ravnine smatraju se paralelnima samo ako nemaju zajedničkih točaka.”, odnosno ne sijeku se međusobno. Da bismo detaljnije zamislili ovu sliku, kao elementarni primjer možemo navesti omjer stropa i poda ili nasuprotnih zidova u zgradi. Odmah postaje jasno o čemu se radi, a potvrđuje se i činjenica da se ove ravnine u uobičajenom slučaju nikada neće presijecati.

Drugi primjer je prozor s dvostrukim ostakljenjem, gdje staklene ploče djeluju kao ravnine. Oni također ni pod kojim uvjetima neće formirati točke međusobnog sjecišta. Osim toga, možete dodati police za knjige, Rubikovu kocku, gdje su ravnine suprotna lica, i druge elemente svakodnevnog života.

Razmatrane ravnine označene su posebnim znakom u obliku dviju ravnih linija "||", koje jasno prikazuju paralelnost ravnina. Dakle, primjenom stvarnih primjera može se formirati jasnija percepcija teme, a samim tim i dalje u razmatranju složenijih pojmova.

Gdje i kako se primjenjuje teorija paralelnih ravnina?

Prilikom proučavanja školskog tečaja geometrije, učenici se moraju nositi s raznovrsnim zadacima, gdje je često potrebno odrediti paralelizam ravnih linija, prave linije i ravnine između sebe ili ovisnost ravnina jedna o drugoj. Analizirajući postojeće stanje, svaki se zadatak može povezati s četiri glavne klase stereometrije.

U prvom razredu nalaze se zadaci u kojima je potrebno odrediti međusobnu paralelnost pravca i ravnine. Njegovo se rješenje svodi na dokaz istoimenog teorema. Da biste to učinili, morate utvrditi da li za liniju koja ne pripada ravnini koja se razmatra postoji paralelna linija koja leži u ovoj ravnini.

U drugu klasu zadataka spadaju oni u kojima se koristi znak paralelnih ravnina. Koristi se za pojednostavljenje postupka dokazivanja, čime se značajno smanjuje vrijeme potrebno za pronalaženje rješenja.

Sljedeći razred pokriva spektar problema o podudarnosti pravaca s glavnim svojstvima paralelnosti ravnina. Rješenje zadataka četvrtog razreda je utvrditi je li ispunjen uvjet paralelnosti ravnina. Znajući točno kako se odvija dokaz određenog problema, učenicima postaje lakše snalaziti se pri primjeni postojećeg arsenala geometrijskih aksioma.

Tako se zadaci čiji uvjet zahtijeva određivanje i dokazivanje paralelnosti pravaca, pravca i ravnine ili dviju ravnina međusobno svode na točan odabir teorema i rješenje prema postojećem skupu pravila.

O paralelnosti pravca i ravnine

Paralelnost pravca i ravnine posebna je tema u stereometriji, budući da je upravo to temeljni pojam na kojem se temelje sva kasnija svojstva paralelnosti geometrijskih likova.

Prema dostupnim aksiomima, u slučaju kada dvije točke pravca pripadaju određenoj ravnini, možemo zaključiti da i zadani pravac leži u njoj. U ovoj situaciji postaje jasno da postoje tri opcije za položaj linije u odnosu na ravninu u prostoru:

1. Pravac pripada ravnini.
2. Za pravac i ravninu postoji jedna zajednička točka presjeka.
3. Ne postoje sjecišne točke pravca i ravnine.

Nas posebno zanima posljednja varijanta, kada nema sjecišta. Tek tada možemo reći da su pravac i ravnina paralelne jedna s drugom. Time je potvrđen uvjet glavnog teorema o predznaku paralelnosti pravca i ravnine koji kaže: "Ako je pravac koji ne pripada dotičnoj ravnini paralelan s bilo kojim pravcem u toj ravnini, tada je dotični pravac također paralelan s danom ravninom."

Potreba za upotrebom znaka paralelizma

Oznaka paralelnosti ravnina obično se koristi za pronalaženje pojednostavljenog rješenja zadataka o ravninama. Suština ovog znaka je sljedeća: Ako postoje dvije crte koje se sijeku u istoj ravnini, paralelne s dvjema linijama koje pripadaju drugoj ravnini, tada se takve ravnine mogu nazvati paralelnim».

Dodatni teoremi

Osim korištenja svojstva koje dokazuje paralelnost ravnina, u praksi se može susresti korištenje još dva dodatna teorema. Prvi je predstavljen u sljedećem obliku: Ako je jedna od dviju paralelnih ravnina paralelna s trećom, tada je i druga ravnina paralelna s trećom ili se s njom potpuno poklapa.».

Na temelju korištenja navedenih teorema uvijek je moguće dokazati paralelnost ravnina u odnosu na promatrani prostor. Drugi teorem prikazuje ovisnost ravnina o okomitoj liniji i ima oblik: “ Ako su dvije nepoklapajuće ravnine okomite na neku ravnu crtu, tada se smatraju međusobno paralelnima».

Pojam nužnog i dovoljnog uvjeta

Uzastopnim rješavanjem zadataka dokazivanja paralelnosti ravnina izveden je potreban i dovoljan uvjet za paralelnost ravnina. Poznato je da je svaka ravnina dana parametarskom jednadžbom oblika: A 1 x+ B 1 y+ C 1 z+D 1 =0. Naš se uvjet temelji na korištenju sustava jednadžbi koje određuju položaj ravnina u prostoru, a predstavljen je sljedećom formulacijom: Da bi se dokazala paralelnost dviju ravnina, potrebno je i dovoljno da sustav jednadžbi koje opisuju te ravnine bude nekonzistentan, odnosno da nema rješenja».

Osnovna svojstva

Međutim, pri rješavanju geometrijskih problema korištenje znaka paralelnosti nije uvijek dovoljno. Ponekad se javlja situacija kada je potrebno dokazati paralelizam dviju ili više linija u različitim ravninama ili jednakost segmenata sadržanih na tim linijama. Da biste to učinili, koristite svojstva paralelnih ravnina. U geometriji ih ima samo dva.

Prvo svojstvo omogućuje procjenu paralelnosti linija u određenim ravninama i predstavljeno je u sljedećem obliku: Ako su dvije paralelne ravnine presječene trećom, tada će linije koje tvore crte presjeka također biti paralelne jedna s drugom».

Značenje drugog svojstva je dokazati jednakost segmenata koji se nalaze na paralelnim linijama. Njegovo tumačenje predstavljeno je u nastavku. " Ako uzmemo u obzir dvije paralelne ravnine i zatvorimo područje između njih, tada se može tvrditi da će duljina segmenata koje tvori ovo područje biti ista».