Pateikite pavyzdžių, kokios plokštumos vadinamos lygiagrečiomis. Plokštumų lygiagretumas: ženklas, sąlyga. Lygiagrečios plokštumos pagal pavyzdžius

Plokštumos padėtis erdvėje nustatoma pagal:

• trys taškai, kurie nėra vienoje tiesėje;
• tiesi linija ir taškas, paimtas už tiesės;
• dvi susikertančios linijos;
• dvi lygiagrečios linijos;
• plokščia figūra.

Pagal tai diagramoje galima nustatyti plokštumą:

• trijų taškų, kurie nėra vienoje tiesėje, projekcijos (3.1 pav., a);
• taško ir tiesės projekcijos (3.1 pav., b);
• dviejų susikertančių tiesių projekcijos (3.1 pav., c);
• dviejų lygiagrečių tiesių projekcijos (3.1 pav., d);
• plokščia figūra (3.1 pav., e);
• lėktuvo pėdsakai;
• didžiausio plokštumos nuolydžio linija.

3.1 pav. – Plokštumų nustatymo metodai

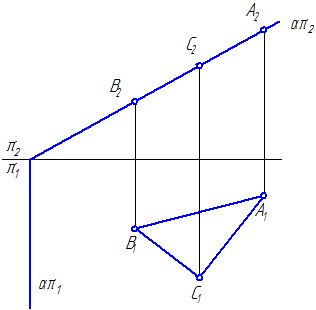
Lėktuvas bendroje padėtyje yra plokštuma, kuri nėra nei lygiagreti, nei statmena jokiai projekcijų plokštumai.

Sekdamas lėktuvu vadinama tiesia linija, gauta susikirtus tam tikrai plokštumai su viena iš projekcijos plokštumų.

Bendrasis lėktuvas gali turėti tris pėdsakus: horizontaliai – απ 1 , priekinis – απ 2 ir profilį – απ 3 , kurį susidaro kertant su žinomomis projekcijų plokštumomis: horizontaliąja π 1, frontaliąja π 2 ir profiliu π 3 (3.2 pav.).

3.2 pav. Bendrosios padėties plokštumos pėdsakai

3.2. Privačios padėties lėktuvai

Privati ​​​​pozicijos plokštuma- plokštuma, statmena arba lygiagreti projekcijų plokštumai.

Plokštuma, statmena projekcijos plokštumai, vadinama projekcijos plokštuma, ir ji bus projektuojama į šią projekcijos plokštumą tiesia linija.

Projekcinės plokštumos savybė: visi taškai, linijos, plokščios figūros, priklausančios išsikišusiai plokštumai, turi projekcijas ant plokštumos pasvirimo(3.3 pav.).

3.3 pav. Priekinė projektavimo plokštuma, kuriai jie priklauso: taškai BET, AT, NUO; linijos AC, AB, saulė; trikampio plokštuma ABC

Priekinės projekcijos plokštuma – priekinei projekcijos plokštumai statmena plokštuma(3.4 pav., a).

Horizontali projekcijos plokštuma – plokštuma, statmena horizontaliai projekcijos plokštumai(3.4 pav., b).

Profilio projektavimo plokštuma – plokštuma, statmena profilinei projekcijų plokštumai.

Plokštumos, lygiagrečios projekcinėms plokštumoms, vadinamos lygio plokštumos arba dvigubai išsikišančios plokštumos.

Priekinė lygio plokštuma – plokštuma, lygiagreti priekinei projekcijos plokštumai(3.4 pav., c).

Horizontali lygio plokštuma – plokštuma, lygiagreti horizontaliai projekcijos plokštumai(3.4 pav., d).

Lygio profilio plokštuma – plokštuma, lygiagreti profilio projekcijos plokštumai(3.4 pav., e).

3.4 pav. – konkrečios padėties plokštumų grafikai

3.3. Taškas ir linija plokštumoje. Priklausymas taškui ir tiesiajai plokštumai

Taškas priklauso plokštumai, jei jis priklauso bet kuriai toje plokštumoje esančiai tiesei(3.5 pav.).

Tiesė priklauso plokštumai, jei ji turi bent du bendrus taškus su plokštuma.(3.6 pav.).

3.5 pav. Priklausymas taškui plokštumoje

α = m // n

D∈ n⇒ D∈ α

3.6 pav. Priklausymas tiesiajai plokštumai

Pratimas

Duota plokštuma, apibrėžta keturkampiu (3.7 pav., a). Būtina užbaigti horizontalią viršūnės projekciją NUO.

a	b

3.7 pav. Uždavinio sprendimas

Sprendimas:

1. ABCD yra plokščias keturkampis, apibrėžiantis plokštumą.
2. Nubrėžkime jame įstrižaines AC ir BD(3.7 pav., b), kurios yra susikertančios linijos, taip pat apibrėžiančios tą pačią plokštumą.
3. Pagal susikirtimo tiesių kriterijų sudarome horizontalią šių linijų susikirtimo taško projekciją - K pagal žinomą priekinę projekciją: A 2 C 2 ∩ B 2 D 2 =K 2 .
4. Atkurkite projekcijos jungties liniją iki sankirtos su horizontalia tiesės projekcija BD: įstrižinėje projekcijoje B 1 D 1 pastatas Į 1 .
5. Per BET 1 Į 1 atliekame įstrižainės projekciją BET 1 NUO 1 .
6. Taškas NUO 1 gauname per projekcinę jungties liniją, kol ji susikerta su horizontalia išplėstos įstrižainės projekcija BET 1 Į 1 .

3.4. Pagrindinės lėktuvo linijos

Plokštumoje galima sukonstruoti begalę linijų, tačiau plokštumoje guli specialios tiesės, vadinamos pagrindinės plokštumos linijos (3.8 - 3.11 pav.).

Tiesus lygis arba plokštuma lygiagreti vadinama tiese, esančia tam tikroje plokštumoje ir lygiagrečia vienai iš projekcinių plokštumų.

Horizontalus arba horizontali lygio linija h(pirmoji lygiagretė) yra tiesė, esanti tam tikroje plokštumoje ir lygiagreti horizontaliai projekcijų plokštumai (π 1)(3.8 pav., a; 3.9).

Priekinės arba priekinis tiesus lygis f(antra lygiagretė) yra tiesė, esanti tam tikroje plokštumoje ir lygiagreti priekinei projekcijų plokštumai (π 2)(3.8 pav., b; 3.10).

Lygio profilio linija p(trečioji lygiagretė) yra tiesė, esanti tam tikroje plokštumoje ir lygiagreti projekcijų profilio plokštumai (π 3)(3.8 pav., c; 3.11).

3.8 pav. a – Horizontali lygio tiesė trikampio pateiktoje plokštumoje

3.8 pav. b – Trikampio nurodytoje plokštumoje esančio lygio priekinė linija

3.8 pav. c – Lygio profilio linija trikampio nurodytoje plokštumoje

3.9 pav. – Horizontali lygio linija plokštumoje, nurodytoje pėdsakais

3.10 pav. Priekinė lygio linija plokštumoje, nurodytoje pėdsakais

3.11 pav. Lygio profilio linija plokštumoje, nurodytoje pėdsakais

3.5. Tiesės ir plokštumos tarpusavio padėtis

Tiesi linija tam tikros plokštumos atžvilgiu gali būti lygiagreti ir turėti su ja bendrą tašką, tai yra, susikirsti.

3.5.1. Tiesios plokštumos lygiagretumas

Tiesios plokštumos lygiagretumo ženklas: tiesė yra lygiagreti plokštumai, jei ji lygiagreti bet kuriai tos plokštumos tiesei(3.12 pav.).

3.12 pav. – Tiesios plokštumos lygiagretumas

3.5.2. Tiesės susikirtimas su plokštuma

Norint sukurti tiesės susikirtimo tašką su bendrosios padėties plokštuma (3.13 pav.), būtina:

1. Uždarykite tiesią liniją aį pagalbinę plokštumą β (kaip pagalbinę plokštumą reikėtų rinktis dalinės padėties plokštumas);
2. Raskite pagalbinės plokštumos β susikirtimo tiesę su duota plokštuma α;
3. Raskite nurodytos linijos susikirtimo tašką a su plokštumų susikirtimo linija MN.

3.13 pav. – Tiesios linijos ir plokštumos susitikimo taško konstravimas

Pratimas

Duota: tiesioginis AB bendroje padėtyje plokštuma σ⊥π 1 . (3.14 pav.). Sukurkite tiesės susikirtimo tašką AB su plokštuma σ.

Sprendimas:

1. Plokštuma σ yra horizontaliai projektuojama, todėl plokštumos σ horizontalioji projekcija yra tiesė σ 1 (horizontalus plokštumos pėdsakas);
2. Taškas Į turi priklausyti linijai AB ⇒ Į 1 ∈BET 1 AT 1 ir duotoji plokštuma σ ⇒ Į 1 ∈σ 1, todėl Į 1 yra projekcijų susikirtimo taške BET 1 AT 1 ir σ1;
3. Priekinės projekcijos taškas Į projekcijos jungties linija randame: Į 2 ∈BET 2 AT 2 .

3.14 pav. Bendrosios padėties linijos sankirta su konkrečios padėties plokštuma

Pratimas

Duota: plokštuma σ = Δ ABC– bendra padėtis, tiesi EF(3.15 pav.).

Būtina sukurti linijos susikirtimo tašką EF su plokštuma σ.

a	b

3.15 pav. – Tiesės susikirtimas su plokštuma

1. Padarykim tiesią liniją EFį pagalbinę plokštumą, kuriai naudosime horizontaliai projektuojančią plokštumą α (3.15 pav., a);
2. Jei α⊥π 1 , tai į projekcijų plokštumą π 1 plokštuma α projektuojama į tiesę (horizontalus plokštumos απ 1 arba α 1 pėdsakas), sutampančią su E 1 F 1 ;
3. Raskime projektuojančios plokštumos α susikirtimo (1-2) tiesę su plokštuma σ (bus svarstomas tokio uždavinio sprendimas);
4. Eilutę (1-2) ir duotą eilutę EF yra toje pačioje plokštumoje α ir susikerta taške K.

Uždavinio sprendimo algoritmas (3.15 pav., b):

Per EF nubrėžkite pagalbinę plokštumą α:

3.6. Matomumo nustatymas konkuruojančių taškų metodu

Vertinant šios tiesės padėtį, reikia nustatyti - kurio tiesės atkarpos taškas yra arčiau (toliau) mums, kaip stebėtojams, žiūrint į projekcijos plokštumą π 1 ar π 2 .

Taškai, priklausantys skirtingiems objektams ir vienoje iš projekcinių plokštumų jų projekcijos sutampa (ty du taškai projektuojami į vieną), vadinami konkuruojančiais šioje projekcijos plokštumoje..

Būtina atskirai apibrėžti matomumą kiekvienoje projekcijos plokštumoje.

Matomumas ties π 2 (3.15 pav.)

Mes pasirenkame taškus, konkuruojančius ant π 2 – taškais 3 ir 4. Tegul taškas 3∈ BC∈σ, taškas 4∈ EF.

Norint nustatyti taškų matomumą projekcijos plokštumoje π 2, reikia nustatyti šių taškų vietą horizontalioje projekcijos plokštumoje žiūrint į π 2 .

Žiūrėjimo į π 2 kryptis rodoma rodykle.

Iš 3 ir 4 taškų horizontalių projekcijų, žvelgiant į π 2, matyti, kad taškas 4 1 yra arčiau stebėtojo nei 3 1 .

4 1 ∈E 1 F 1 ⇒ 4∈EF⇒ 4 taškas bus matomas ant π 2, gulint ant linijos EF, taigi tiesi linija EF nagrinėjamų konkuruojančių taškų vietoje yra prieš plokštumą σ ir bus matomas iki taško K

Matomumas ties π 1

Matomumui nustatyti pasirenkame taškus, kurie varžosi π 1 – taškais 2 ir 5.

Norint nustatyti taškų matomumą projekcijos plokštumoje π 1, reikia nustatyti šių taškų vietą priekinėje projekcijos plokštumoje žiūrint į π 1 .

Žiūrėjimo į π 1 kryptis rodoma rodykle.

Iš 2 ir 5 taškų frontalinių projekcijų, žvelgiant į π 1, matyti, kad taškas 2 2 yra arčiau stebėtojo nei 5 2 .

2 1 ∈BET 2 AT 2 ⇒ 2∈AB⇒ 2 taškas bus matomas ant π 1, gulėdamas ant linijos AB, taigi tiesi linija EF nagrinėjamų konkuruojančių taškų atkarpoje yra po plokštuma σ ir bus nematomas iki taško K yra tiesės susikirtimo su plokštuma σ taškai.

Matomas iš dviejų konkuruojančių taškų bus tas, kurio „Z“ arba (ir) „Y“ koordinatė yra didesnė.

3.7. Tiesios plokštumos statmena

Tiesios plokštumos statmenumo ženklas: Tiesė yra statmena plokštumai, jei ji yra statmena dviem susikertančioms tiesėms, esančioms duotoje plokštumoje.

a	b

3.16 pav. – tiesės, statmenos plokštumai, nustatymas

Teorema. Jei tiesė yra statmena plokštumai, tada diagramoje: horizontali tiesės projekcija yra statmena horizontaliai horizontaliai plokštumos projekcijai, o tiesės priekinė projekcija yra statmena frontalinei projekcijai (3.16 pav., b)

Teorema įrodoma per stačiojo kampo projekcijos teoremą konkrečiu atveju.

Jeigu plokštuma duota pėdsakais, tai plokštumai statmenos tiesės projekcijos yra statmenos atitinkamiems plokštumos pėdsakams (3.16 pav., a).

Tegul linija p statmena plokštumai σ=Δ ABC ir eina per tašką K.

1. Plokštumoje σ=Δ pastatykime horizontaliąją ir frontalinę ABC : A-1∈σ; A-1//π 1 ; C-2∈σ; C-2//π 2 .
2. Atkurti iš taško K statmenai nurodytai plokštumai: p1⊥h1 ir p2⊥f2, arba p1⊥απ 1 ir p2⊥απ 2

3.8. Dviejų plokštumų tarpusavio padėtis

3.8.1. Plokštumos lygiagretumas

Dvi plokštumos gali būti lygiagrečios ir susikertančios viena su kita.

Dviejų plokštumų lygiagretumo ženklas: Dvi plokštumos yra viena kitai lygiagrečios, jei dvi susikertančios vienos plokštumos tiesės yra atitinkamai lygiagrečios dviem susikertančioms kitos plokštumos tiesėms.

Pratimas

Duota plokštuma bendrojoje padėtyje α=Δ ABC ir taškas F∉α (3.17 pav.).

Per tašką F nubrėžkite plokštumą β lygiagrečią plokštumai α.

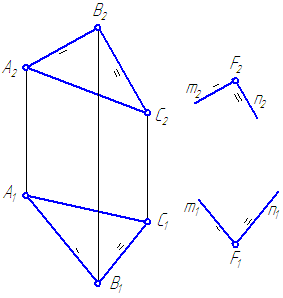
3.17 pav. Plokštumos, lygiagrečios duotajam, konstravimas

Sprendimas:

Kaip susikertančias plokštumos α tieses imame, pavyzdžiui, trikampio AB ir BC kraštines.

1. Per tašką F nubrėžti tiesią liniją m, lygiagrečiai, pvz. AB.
2. Per tašką F, arba per bet kurį tašką, priklausantį m, nubrėžkite tiesią liniją n, lygiagrečiai, pvz. saulė, be to m∩n=F.
3. β = m∩n ir β//α pagal apibrėžimą.

3.8.2. Plokštumų sankirta

2 plokštumų susikirtimo rezultatas yra tiesi linija. Bet kuri tiesi linija plokštumoje arba erdvėje gali būti vienareikšmiškai apibrėžta dviem taškais. Todėl norint sukurti dviejų plokštumų susikirtimo liniją, reikia rasti du abiem plokštumoms bendrus taškus ir tada juos sujungti.

Apsvarstykite dviejų plokštumų susikirtimo pavyzdžius su skirtingais jų patikslinimo būdais: pėdsakai; trys taškai, kurie nėra vienoje tiesėje; lygiagrečios linijos; susikertančios linijos ir kt.

Pratimas

Dvi plokštumos α ir β pateiktos pėdsakais (3.18 pav.). Sukurkite plokštumų susikirtimo liniją.

3.18 pav. Plokštumų susikirtimas bendroje padėtyje, pateiktas pėdsakais

Plokštumų susikirtimo linijos sudarymo procedūra:

1. Raskite horizontalių pėdsakų susikirtimo tašką – tai taškas M(jos projekcijos M 1 ir M 2, tuo tarpu M 1 =M, nes M - tam tikros padėties taškas, priklausantis plokštumai π 1).
2. Raskite priekinių pėdsakų susikirtimo tašką – tai taškas N(jos projekcijos N 1 ir N 2, tuo tarpu N 2 = N, nes N- tam tikros padėties taškas, priklausantis plokštumai π 2).
3. Sukurkite plokštumų susikirtimo liniją, sujungdami gautų taškų projekcijas tuo pačiu pavadinimu: M 1 N 1 ir M 2 N 2 .

MN- plokštumų susikirtimo linija.

Pratimas

Plokštuma σ = Δ ABC, plokštuma α yra horizontaliai projektuojama (α⊥π 1) ⇒α 1 yra horizontalus plokštumos pėdsakas (3.19 pav.).

Sukurkite šių plokštumų susikirtimo liniją.

Sprendimas:

Kadangi plokštuma α kerta kraštines AB ir AC trikampis ABC, tada susikirtimo taškai K ir Lšių kraštinių su plokštuma α yra bendros abiem duotoms plokštumoms, o tai leis jas sujungus rasti reikiamą susikirtimo liniją.

Taškai gali būti rasti kaip tiesių susikirtimo taškai su projektavimo plokštuma: raskite horizontalias taškų projekcijas K ir L, tai yra K 1 ir L 1 , duotosios plokštumos α horizontalaus pėdsako (α 1) sankirtoje su horizontaliomis kraštinių projekcijomis Δ ABC: BET 1 AT 1 ir A 1 C vienas . Tada, naudodamiesi projekcinio ryšio linijomis, randame šių taškų frontalines projekcijas K2 ir L 2 ant priekinių tiesių projekcijų AB ir AC. Sujungkime to paties pavadinimo projekcijas: K 1 ir L 1 ; K2 ir L 2. Nutiesta duotųjų plokštumų susikirtimo linija.

Problemos sprendimo algoritmas:

KL– susikirtimo linija Δ ABC ir σ (α∩σ = KL).

3.19 pav. Bendrosios ir konkrečios padėties plokštumų sankirta

Pratimas

Duotos plokštumos α = m//n ir plokštuma β = Δ ABC(3.20 pav.).

Sukurkite nurodytų plokštumų susikirtimo liniją.

Sprendimas:

1. Norint rasti taškus, bendrus abiem duotoms plokštumoms ir apibrėžti plokštumų α ir β susikirtimo liniją, reikia naudoti konkrečios padėties pagalbines plokštumas.
2. Kaip tokias plokštumas pasirenkame dvi tam tikros padėties pagalbines plokštumas, pvz.: σ // τ; σ⊥π 2; τ⊥π 2 .
3. Naujai įvestos plokštumos susikerta su kiekviena iš nurodytų plokštumų α ir β išilgai tiesių linijų, lygiagrečių viena kitai, nes σ // τ:

- plokštumų α, σ ir τ susikirtimo rezultatas yra tiesės (4-5) ir (6-7);

- plokštumų β, σ ir τ susikirtimo rezultatas yra linijos (3-2) ir (1-8).

1. Tiesios linijos (4-5) ir (3-2) yra plokštumoje σ; susikirtimo taškas M vienu metu yra plokštumose α ir β, tai yra, šių plokštumų susikirtimo linijoje;
2. Panašiai randame esmę N, bendras plokštumose α ir β.
3. Sujungus taškus M ir N, statome plokštumų α ir β susikirtimo liniją.

3.20 pav. Dviejų plokštumų sankirta bendroje padėtyje (bendras atvejis)

Problemos sprendimo algoritmas:

Pratimas

Plokštumos α = Δ ABC ir β = a//b. Sukonstruoti duotųjų plokštumų susikirtimo liniją (3.21 pav.).

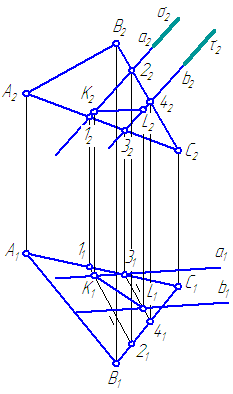
3.21 pav. Plokštumų susikirtimo uždavinio sprendimas

Sprendimas:

Naudokime pagalbines privačios padėties sekantines plokštumas. Juos pristatome taip, kad sumažėtų konstrukcijų skaičius. Pavyzdžiui, pristatykime plokštumą σ⊥π 2 , apimančią tiesę aį pagalbinę plokštumą σ (σ∈ a). Plokštuma σ kerta plokštumą α išilgai tiesės (1-2), o σ∩β= a. Taigi (1-2)∩ a=K.

Taškas Į priklauso abiem plokštumoms α ir β.

Iš čia ir esmė K, yra vienas iš norimų taškų, per kurį eina duotųjų plokštumų α ir β susikirtimo linija.

Norėdami rasti antrąjį tašką, priklausantį α ir β susikirtimo linijai, sudarome tiesę bį pagalbinę plokštumą τ⊥π 2 (τ∈ b).

Sujungus taškus K ir L, gauname plokštumų α ir β susikirtimo liniją.

3.8.3. Viena kitai statmenos plokštumos

Plokštumos yra viena kitai statmenos, jei viena iš jų eina per statmeną kitai.

Pratimas

Duota plokštuma σ⊥π 2 ir tiesė bendroje padėtyje - DE(3.22 pav.)

Būtina sukurti per DE plokštuma τ⊥σ.

Sprendimas.

Nubrėžkime statmeną CDį plokštumą σ – C 2 D 2 ⊥σ 2 (pagal ).

3.22 pav. Plokštumos, statmenos duotai plokštumai, konstrukcija

Pagal stačiojo kampo projekcijos teoremą C 1 D 1 turi būti lygiagreti projekcijos ašiai. susikertančios linijos CD∩DE apibrėžkite plokštumą τ. Taigi, τ⊥σ.

Panašūs samprotavimai, kalbant apie plokštumą bendroje padėtyje.

Pratimas

Plokštuma α = Δ ABC ir taškas K už plokštumos α.

Būtina sukurti plokštumą β⊥α, einanti per tašką K.

Sprendimo algoritmas(3.23 pav.):

1. Pastatykime horizontalią h ir priekinės f duotoje plokštumoje α = Δ ABC;
2. Per tašką K nubrėžkite statmeną bį plokštumą α (pagal statmens plokštumai teorema: jei linija statmena plokštumai, tai jos projekcijos yra statmenos plokštumoje esančioms horizontalės ir priekinės dalies įstrižoms projekcijoms:b 2⊥f2; b 1⊥h1;
3. Plokštumą β nustatome bet kokiu būdu, pavyzdžiui, β = a∩b, taigi statmena duotajai plokštuma sudaroma: α⊥β.

3.23 pav. Plokštumos, statmenos duotam Δ, konstravimas ABC

3.9. Savarankiško sprendimo užduotys

1. Plokštuma α = m//n(3.24 pav.). Yra žinoma, kad K∈α.

Nubraižykite priekinę taško projekciją Į.

3.24 pav

2. Sukonstruoti atkarpa duotos tiesės pėdsakus CB, ir nustatyti kvadrantus, pro kuriuos jis praeina (3.25 pav.).

3.25 pav

3. Sukurkite kvadrato, priklausančio plokštumai α⊥π 2 projekcijas, jei jos įstrižainė MN//π 2 (3.26 pav.).

3.26 pav

4. Sukonstruoti stačiakampį ABCD su didesne puse saulė tiesioje linijoje m, remiantis sąlyga, kad jo kraštinių santykis yra 2 (3.27 pav.).

3.27 pav

5. Plokštuma α= a//b(3.28 pav.). Sukurkite plokštumą β, lygiagrečią plokštumai α ir 20 mm atstumu nuo jos.

3.28 pav

6. Plokštuma α=∆ ABC ir taškas D D plokštuma β⊥α ir β⊥π 1 .

7. Duota plokštuma α=∆ ABC ir taškas D iš lėktuvo. Konstruoti per tašką D tiesioginis DE//α ir DE//π 1 .

Plokštumos lygiagretumas. Jei dvi susikertančios vienos plokštumos tiesės yra atitinkamai lygiagrečios dviem susikertančioms kitos plokštumos tiesėms, tai šios plokštumos yra lygiagrečios.
Įrodymas. Leisti a ir b- lėktuvo duomenys, a 1 ir a 2- tiesios linijos plokštumoje a, susikerta taške A, b 1 ir b 2 joms lygiagrečios tiesės plokštumoje b. Tarkime, kad lėktuvai a ir b ne lygiagrečiai, tai yra, jie susikerta išilgai tiesės Su. Tiesiai a 1 lygiagreti linijai b 1, taigi jis yra lygiagretus pačiai plokštumai b(tiesės ir plokštumos lygiagretumo ženklas). Tiesiai a 2 lygiagrečiai linijai b2, taigi ji lygiagreti pačiai plokštumai. b(tiesės ir plokštumos lygiagretumo ženklas). Tiesiai Su priklauso lėktuvui a, taigi bent viena iš eilučių a 1 arba a 2 kerta liniją Su, tai yra, jis turi bendrą tašką su juo. Bet tiesiai Su taip pat priklauso lėktuvui b, o tai reiškia, kad kertant liniją Su, tiesiai a 1 arba a 2 kerta lėktuvą b, kurio negali būti, nes tiesioginis a 1 ir a 2 lygiagrečiai plokštumai b. Iš to išplaukia, kad lėktuvai a ir b nesikerta, tai yra, jie yra lygiagretūs.

1 teorema . Jei dvi lygiagrečios plokštumos susikerta su trečiąja, tada susikirtimo linijos yra lygiagrečios.
Įrodymas. Leisti a ir b yra lygiagrečios plokštumos ir g - plokštuma, kuri juos kerta. Lėktuvas a susikerta su plokštuma g tiesia linija a. Lėktuvas b susikerta su plokštuma g tiesia linija b. Sankirtos linijos a ir b gulėti toje pačioje plokštumoje g ir todėl gali būti arba susikertančios, arba lygiagrečios tiesės. Tačiau, priklausydami dviem lygiagrečioms plokštumoms, jie negali turėti bendrų taškų. Todėl jie yra lygiagretūs.

2 teorema. Lygiagrečių linijų atkarpos, uždarytos tarp dviejų lygiagrečių plokštumų, yra lygios.
Įrodymas. Leisti a ir b yra lygiagrečios plokštumos ir a ir b yra lygiagrečios tiesės, kurios jas kerta. Per tiesias linijas a ir b išleisime lėktuvas g (Šios linijos yra lygiagrečios, todėl apibrėžti plokštumą ir tik vieną). Lėktuvas a susikerta su plokštuma g tiesė AB . Lėktuvas b susikerta su plokštuma g išilgai tiesės SD. Pagal ankstesnę teoremą tiesė Su lygiagreti tiesia linija d. Tiesioginis a,b, AB ir SD priklauso lėktuvui g.Šių tiesių ribojamas keturkampis yra lygiagretainis (jo priešingos kraštinės lygiagrečios). Ir kadangi tai yra lygiagretainis, tada jo priešingos kraštinės yra lygios, tai yra AD \u003d BC

Nagrinėjamas plokštumų lygiagretumo ryšys, jo savybės ir pritaikymai.

Vizualus dviejų vietos vaizdas

Plokštumos suteikia modeliavimą naudojant gretimų sienų paviršių plokštumas, kambario lubas ir grindis, dviaukštes lovas, du pritvirtintus popieriaus lapus

magai ir kt. (242-244 pav.).

Nors yra begalė įvairių plokštumų santykinės padėties variantų, kurių nustatymui ir apibūdinimui vėliau bus taikomi kampų ir atstumų matavimai, pirmiausia apsistosime ties tų, kuriose klasifikacija (taip pat ir tiesės su plokštumomis) yra pagrįstas jų bendrų taškų skaičiumi.

1. Dvi plokštumos turi bent tris bendrus taškus, kurie nėra toje pačioje tiesėje. Tokios plokštumos sutampa (aksioma С 2, §7).

2. Dviejų plokštumų bendrieji taškai yra vienoje tiesėje, kuri yra šių plokštumų susikirtimo linija (aksioma C 3, § 7). Šios plokštumos susikerta.

3. Abi plokštumos neturi bendrų taškų.

AT šiuo atveju jie vadinami lygiagrečiai -

Dvi plokštumos vadinamos lygiagrečiomis, jei jos neturi bendrų taškų.

Plokštumų lygiagretumas žymimas ||: α || β.

Kaip visada, pristatant geometrines sąvokas,

Yra problemų dėl jų egzistavimo. Kryžiaus egzistavimas

plokštumos yra būdingas erdvės bruožas,

ir jau ne kartą naudojome. Mažiau akivaizdu

lygiagrečių plokštumų egzistavimas. Nėra

abejoja, kad, pavyzdžiui, priešingų veidų plokštumos

kubeliai yra lygiagretūs jai, tai yra, jie nesikerta. Bet iš karto

Žinoma, pagal apibrėžimą to nustatyti neįmanoma. Už sprendimą

iškeltą klausimą, taip pat kitus su tuo susijusius klausimus

plokštumų lygiagretumas, būtina turėti lygiagretumo ženklą.

Norint ieškoti ženklo, patartina atsižvelgti į lėktuvą,

„austa“ iš tiesių linijų. Akivaizdu, kad kiekviena eilutė iš

lygiagrečios plokštumos turi būti lygiagrečios kitai.

Priešingu atveju plokštumos turės bendrą tašką. Dosta-

Ar plokštumos β lygiagrečiai tiksliai su viena tiesi plokštuma α

kad plokštumos α ir β būtų lygiagrečios? Besąlyginis

bet ne (pagrįskite!). Praktinė patirtis rodo

pakanka dviejų tokių susikertančių tiesių. Prisegti

ant stiebo lygiagreti žemei platforma, užtenka ją pastatyti

yra lygiagrečios antrajai plokštumai, tada šios plokštumos yra lygiagrečios.

 Plokštumos α susikertančios tiesės a ir b bus lygiagrečios plokštumai β. Įrodykime, kad plokštumos α ir β yra lygiagrečios prieštaravimu. Tam darome prielaidą, kad plokštumos α ir β susikerta išilgai tiesės

t (246 pav.). Tiesės a ir b negali susikirsti su tiesės m pagal prielaidą. Tačiau tada plokštumoje α per vieną tašką nubrėžiamos dvi tiesės, kurios nesikerta su tiese m, tai yra lygiagrečios jai. Tai prieštaravimas

ir užbaigia teoremos įrodymą.

Plokštumų lygiagretumo ženklas naudojamas plokščių konstrukcijų (betoninių plokščių, grindų, diskinių goniometrų ir kt.) horizontaliam išdėstymui naudojant du lygius, išdėstytus konstrukcijos plokštumoje ant susikertančių linijų. Remdamiesi šia funkcija, galite sukurti plokštumą, lygiagrečią nurodytai.

Užduotis 1. Per tašką, esantį už duotosios plokštumos, nubrėžkite plokštumą, lygiagrečią duotajai.

 Plokštuma β ir taškas M pateikti už plokštumos ribų (247 pav., a). Per tašką M nubrėžkite dvi susikertančias tieses a ir b, lygiagrečias plokštumai β. Norėdami tai padaryti, plokštumoje β reikia paimti dvi susikertančias tieses c ir d (247 pav., b). Tada per tašką M nubrėžkite tieses a ir b, lygiagrečias tiesėms c ir d.

bet (247 pav., c).

Susikertančios tiesės a ir b yra lygiagrečios plokštumai β, pagal tiesės ir plokštumos lygiagretumo kriterijų (1 teorema §11). Jie vienareikšmiškai apibrėžia plokštumą α. Pagal įrodytą kriterijų α || β.

1 pavyzdys. Duotas kubas ABCDA 1 B 1 C 1 D 1, taškai M, N, P yra atitinkamai briaunų BC, B 1 C 1, A 1 D 1 vidurio taškai. Nustatykite santykinę plokštumų padėtį: 1) ABB 1 ir PNM; 2) NMA ir A 1 C 1 C ; 3) 1 NM

ir PC 1 C ; 4) MAD 1 ir DB 1 C.

 1) Plokštumos ABB 1 ir РNM (248 pav.) yra lygiagrečios, remiantis plokštumų lygiagretumu (1 teorema). Iš tiesų, tiesės PN ir NM susikerta ir yra lygiagrečios plokštumai ABB 1, tiesės ir plokštumos lygiagretumo ženklu (11 § 1 teorema), nes atkarpos PN ir NM jungia priešingų kraštinių vidurio taškus. kvadratai, todėl jie yra lygiagrečiai kvadratų kraštinėms:

PN || A 1 B 1 , NM || 1 B.

2) Plokštumos NMA ir A 1 C 1 C susikerta išilgai tiesės AA 1 (249 pav.). Iš tiesų, tiesės AA 1 ir CC 1 yra lygiagrečios pagal lygiagrečių tiesių ženklą (AA 1 || BB 1 , BB 1 || CC 1 ). Todėl tiesė AA 1 yra plokštumoje A 1 C 1 C . Panašiai pateisinamas ir AA 1 linijos priklausymas plokštumai NMA.

3) Plokštumos A 1 NM ir PC 1 C (250 pav.) yra lygiagrečios, remiantis plokštumų lygiagretumu. Iš tiesų, NM || Su 1 C. Todėl tiesė NM lygiagreti plokštumai PC 1 C. Atkarpos PC 1 ir A 1 N taip pat lygiagrečios, nes keturkampis PC 1 NA 1 yra lygiagretainis (A 1 P || NC 1 , A 1 P = NC 1). Taigi tiesė A 1 N lygiagreti plokštumai PC 1 C. Tiesės A 1 N ir NM susikerta.

4) Plokštumos MAD 1 ir DB 1 C susikerta (251 pav.). Nors nubrėžti jų susikirtimo liniją nėra lengva, vieną šios linijos tašką nurodyti nesunku. Iš tiesų, tiesės A 1 D ir B 1 C yra lygiagrečios, nes keturkampis A 1 B 1 CD yra lygiagretainis (A 1 B 1 \u003d AB \u003d CD, A 1 B 1 || AB, AB || CD) . Todėl tiesė A 1 D priklauso plokštumai DB 1 C. Tiesės A 1 D ir AD 1 susikerta taške, bendrame plokštumoms MAD 1 ir DB 1 C.

Jei dvi susikertančios vienos plokštumos tiesės yra atitinkamai lygiagrečios dviem kitos plokštumos tiesėms, tai šios plokštumos yra lygiagrečios.

Naudojant tiesės ir plokštumos lygiagretumo ženklą (1 teorema §11), nesunku nustatyti, kad 1 teoremos sąlyga išplaukia iš 1 teoremos sąlygos. ′.

Natūralu, kad kyla klausimas dėl 1 uždavinyje pateiktos konstrukcijos unikalumo. Kadangi šią savybę turėsime naudoti ne vieną kartą, ją atskiriame kaip atskirą teoremą. Tačiau pirmiausia apsvarstykite kitą teiginį.

2 teorema (dėl dviejų lygiagrečių plokštumų susikirtimo su trečdaliu).

Jei dvi lygiagrečias plokštumas kerta trečioji plokštuma, tai plokštumų susikirtimo linijos yra lygiagrečios.

 Tegu pateiktos lygiagrečios plokštumos α, β ir jas kertanti plokštuma γ (252 pav.). Pažymėkite susikirtimo linijas

per a ir b. Šios linijos yra plokštumoje γ ir nesikerta, nes plokštumos α ir β neturi bendrų taškų. Todėl tiesioginis

mano a ir b yra lygiagrečios.

3 teorema (apie duotajai lygiagrečios plokštumos egzistavimą ir unikalumą).

Per tašką, esantį už tam tikros plokštumos, yra tik viena plokštuma, lygiagreti nurodytai plokštumai.

 Tokios plokštumos konstrukcija atliekama 1 uždavinyje. Konstrukcijos unikalumą įrodysime prieštaravimu. Tarkime, kad per tašką M nubrėžtos dvi skirtingos plokštumos α ir γ, pa-

lygiagrečios plokštumos β (253 pav.), o tiesė m – jų susikirtimo linija. Per tašką M nubrėžkime plokštumą δ, susikertančią su tiese

m ir plokštuma β (kaip tai galima padaryti?). Pažymėkite a ir b

plokštumos δ susikirtimo tiesė su plokštumomis α ir γ, o per c - plokštumų δ ir β susikirtimo tiesė (253 pav.). Pagal 2 teoremą ir || Su

ir b || Su. Tai yra, δ plokštumoje per

tašką M kerta dvi tiesės, lygiagrečios tiesei c. Prieštaravimas rodo prielaidos neteisingumą.

Plokštumų lygiagretumo santykis turi nemažai savybių, kurios turi analogų planimetrijoje.

4 teorema (apie lygiagrečių tiesių atkarpas tarp lygiagrečių plokštumų).

Lygiagrečių plokštumų nupjautų lygiagrečių tiesių atkarpos yra lygios viena kitai.

 Tegul dvi lygiagrečios plokštumos α ir β bei atkarpos AB

ir CD lygiagrečios tiesės a ir d, nupjautos šių plokštumų (254 pav., a). Per tieses a ir d nubrėžkime plokštumą γ (254 pav., b). Jis kerta plokštumas α ir β išilgai tiesių AC ir BD, kurios pagal 2 teoremą yra lygiagrečios. Todėl keturkampis ABCD yra lygiagretainis, jo priešingos kraštinės AC ir BD yra lygios.

Iš aukščiau pateiktos savybės išplaukia, kad jei atidėtume nuo visų plokštumos taškų

lygiagrečios vienodo ilgio atkarpos vienoje plokštumos pusėje, tada šių atkarpų galai sudaro dvi lygiagrečias plokštumas. Būtent šia savybe remiasi gretasienio konstrukcija segmentų nusodinimo būdu (255 pav.).

5 teorema (apie plokštumų lygiagretumo santykio tranzityvumą).

Jei kiekviena iš dviejų plokštumų yra lygiagreti trečiajai, tai šios dvi plokštumos yra lygiagrečios viena kitai.

 Tegu plokštumos α ir β lygiagrečios plokštumai γ. Tarkime, kad

α ir β nėra lygiagrečios. Tada plokštumos α ir β turi bendrą tašką, o per šį tašką eina dvi skirtingos plokštumos ir yra lygiagrečios plokštumai γ, o tai prieštarauja 3 teoremai. Todėl plokštumos α ir β neturi bendrų taškų, tai yra lygiagrečiai.

5 teorema yra dar vienas plokštumų lygiagretumo požymis. Jis plačiai naudojamas tiek geometrijoje, tiek praktinėje veikloje. Pavyzdžiui, daugiabutyje grindų ir lubų plokštumų lygiagretumas kiekviename aukšte garantuoja jų lygiagretumą skirtinguose aukštuose.

2 uždavinys. Įrodykite, kad jei tiesė a kerta plokštumą α, tai ji taip pat kerta kiekvieną plokštumai lygiagrečią plokštumai α.

 Tegul plokštumos α ir β yra lygiagrečios, o tiesė a kerta plokštumą α taške A. Įrodykime, kad jis taip pat kerta plokštumą

β. Tarkime, kad taip nėra. Tada tiesė a lygiagreti plokštumai β. Per tiesę a nubrėžkime plokštumą γ ir savavališką plokštumos β tašką (256 pav.).

Ši plokštuma kerta lygiagrečias plokštumas α ir β išilgai tiesių b ir c. bendrai

pagal 2 teoremą, b || c, tai yra, plokštumoje γ per tašką A eina dvi tiesės a ir b lygiagrečios tiesei c . Šis prieštaravimas patvirtina teiginį.

Pabandykite patys įrodyti, kad jei plokštuma α kerta plokštumą β, tai ji taip pat kerta kiekvieną plokštumą, lygiagrečią plokštumai β.

2 pavyzdys. Tetraedro ABCD taškai K, F, E yra kraštinių DA, DC, DB vidurio taškai, o M ir P yra atitinkamai paviršių ABD ir BCD masės centrai.

1) Nustatyti santykinę plokštumų KEF ir ABC padėtį;

DEF ir ABC.

2) Nustatyti plokštumų AFB ir KEC susikirtimo liniją.

3) Raskite tetraedro skerspjūvio plotą plokštuma, lygiagrečia plokštumai ABD ir einančia per tašką P, jei visos tetraedro briaunos lygios a.

 Pastatykime vaizdą atitinkantį sąlygą (257 pav., a). 1) Plokštumos KEF ir ABC yra lygiagrečios, remiantis plokštumų lygiagretumu (1 teorema '): KEF plokštumos susikertančios tiesės KE ir KF yra lygiagrečios plokštumos ABC susikertančioms tiesėms AB ir AC. atitinkamos vidurio linijos

trikampių piešimas).

Plokštumos DEF ir ABC susikerta išilgai tiesės BC, nes tiesė BC priklauso abiem plokštumoms, ir jos negali sutapti – taškai A, B, C, D nėra toje pačioje plokštumoje.

2) Plokštuma AFB kertasi su plokštuma KEC išilgai tiesės, kurioje yra taškas P, nes šiose plokštumose esančios tiesės CE ir BF yra plokštumoje BCD ir susikerta taške P. Kitas taškas – tiesių AF ir CK susikirtimo taškas Q plokštumoje ACD (257 pav., b). Akivaizdu, kad šis taškas yra ACD paviršiaus masės centras. Norima sankryža yra linija PQ.

3) Pastatykime sąlygoje nurodytą atkarpą, naudodami plokštumų lygiagretumo ženklą. Per taškus P ir Q nubrėžkime tieses, lygiagrečias tiesėms DB ir DA (257 pav., c). Šios tiesės kerta atkarpą CD taške L. Pastaroji išplaukia iš trikampio masės centro savybės – ji padalija trikampio medianas santykiu 2:1, skaičiuojant nuo viršūnės. Belieka pritaikyti Talio teoremą. Taigi plokštumos PLQ ir BDA yra lygiagrečios. Norima atkarpa yra trikampis LSN.

Pagal konstrukciją trikampiai BCD ir SCL yra panašūs su panašumo koeficientu CE CP = 3 2 . Todėl LS = 3 2 BD . Panašiai,

pridedamos lygybės: LN = 3 2 AD , NS = 3 2 AB . Tai reiškia, kad trikampiai LSN ir ABD yra panašūs su panašumo koeficientu 3 2 . Pagal panašių trikampių plotų savybes,

S LNS = 4 9 S ABD . Belieka rasti trikampio ABD plotą. pagal-

kadangi, darant prielaidą, visos tetraedro briaunos lygios a, tai S ABD = 4 3 a 2 .

Norimas plotas yra 3 1 3 a 2 .

Tikslinga atkreipti dėmesį į tai, kad atsakymas priklauso tik nuo ABD aspekto srities. Todėl visų kraštinių lygybė yra tik priemonė šiai sričiai rasti. Taigi šią problemą galima iš esmės apibendrinti.

Atsakymas. 1) KEF || ABC; 3) 3 1 3 a 2 .

 Kontroliniai klausimai

1. Ar tiesa, kad dvi plokštumos yra lygiagrečios, jei kiekviena tiesė vienoje plokštumoje lygiagreti kitai plokštumai?

2. Plokštumos α ir β yra lygiagrečios. Ar šiose plokštumose yra susikertančių linijų?

3. Dvi trikampio kraštinės lygiagrečios kokiai nors plokštumai. Ar trečioji trikampio kraštinė lygiagreti šiai plokštumai?

4. Dvi lygiagretainio kraštinės lygiagrečios kokiai nors plokštumai. Ar tiesa, kad lygiagretainio plokštuma lygiagreti duotajai plokštumai?

5. Ar dviejų lygiagrečių plokštumų nupjautų tiesių atkarpos gali būti nelygios?

6. Ar kubo skerspjūvis gali būti lygiašonė trapecija? Ar kubo pjūvis gali būti taisyklingas penkiakampis? Ar tiesa, kad dvi plokštumos, lygiagrečios tai pačiai tiesei, yra lygiagrečios viena kitai?

Plokštumų α ir β susikirtimo su plokštuma γ linijos yra lygiagrečios viena kitai. Ar α ir β plokštumos lygiagrečios?

Ar trys kubo briaunos gali būti lygiagrečios tai pačiai plokštumai?

Grafiniai pratimai

1. 258 paveiksle pavaizduotas kubas ABCDA 1 B 1 C 1 D 1 , taškai M , N , K , L , P yra atitinkamų briaunų vidurio taškai. Pagal pateiktą pavyzdį užpildykite lentelę, pasirinkdami reikiamą plokštumų α ir β išdėstymą.

Abipusis

vieta

α || β α = β

α × β α || β α = β

2. Pav. 259 parodytas tetraedras ABCD, taškai K, F, M, N, Q yra atitinkamų briaunų vidurio taškai. Nurodykite:

1) plokštuma, einanti per tašką K, lygiagreti plokštumai ABC;

2) plokštuma, einanti per tiesę BD, lygiagrečią plokštumai MNQ.

3. Nustatykite, kokia yra plokštumos, einančios per pateiktus tris paveikslėlyje parodytus taškus, figūros pjūvis.

kah 260, a)–e) ir 261, a)–d).

4. Pagal duotus duomenis pastatykite brėžinį.

1) Iš lygiagretainio ABCD viršūnių, esančių vienoje iš dviejų lygiagrečių plokštumų, brėžiamos lygiagrečios tiesės, kurios atitinkamai kerta antrąją plokštumą taškuose A 1 , B 1 , C 1 , D 1 .

2) Trikampis A 1 B 1 C 1 yra trikampio ABC projekcija į jam lygiagrečią plokštumą α. Taškas M yra BC vidurys, M 1 yra taško M projekcija į plokštumą α.

207. Kubo ABCDA 1 B 1 C 1 D 1 taškai O , O 1 yra atitinkamai veidų ABCD ir A 1 B 1 C 1 D 1 centrai, M – briaunos AB vidurio taškas.

1°) Nustatykite santykinę plokštumų MO 1 O padėtį

ir ADD 1 , ABD 1 ir CO 1 C 1 .

2°) Sukurkite plokštumos DCC 1 ir tiesės MO 1 susikirtimo tašką bei plokštumų MCC 1 ir A 1 D 1 C 1 susikirtimo liniją.

3) Raskite kubo skerspjūvio plotą plokštuma, lygiagrečia plokštumai AD 1 C 1 ir einančia per tašką O 1, jei kubo kraštas yra a.

208. Tetraedre ABCD taškai K , L , P yra atitinkamai paviršių ABD , BDC , ABC masės centrai, o M yra briaunos AD vidurio taškas.

1°) Nustatykite santykinę ACD plokštumų padėtį

ir KLP; MLK ir ABC.

2°) Nustatyti plokštumos ABC ir tiesės ML susikirtimo tašką bei plokštumų MKL ir ABC susikirtimo liniją.

3) Raskite tetraedro skerspjūvio plotą plokštumoje, einančioje per taškus K, L ir M, lygiagrečią tiesei AD, jei visos tetraedro briaunos lygios a.

209. Duotas kubas ABCDA 1 B 1 C 1 D 1 . Taškai L, M, M 1 yra atitinkamai kraštinių AB, AD ir A 1 D 1 vidurio taškai.

1°) Nustatykite plokštumų B 1 D 1 D santykinę padėtį

ir LMM1.

2) Sukurkite plokštumą, einančią per tašką M, lygiagrečią plokštumai ACC 1 .

3) Sukurkite kubo atkarpą plokštuma, einančia per tašką M 1, lygiagrečią plokštumai CDD 1 .

4) Nustatykite santykinę plokštumų MA 1 IN 1 padėtį

ir CDM1.

5) Sukurkite plokštumą, einančią per tiesę C 1 D 1, lygiagrečią plokštumai CDM 1 .

210. Taisyklingoje keturkampėje piramidėje SABCD visos briaunos yra lygios viena kitai. Taškai L , M ir N yra atitinkamai kraštinių AS , BS , CS vidurio taškai.

1°) Nustatykite: tiesių LM ir BC santykinę padėtį; tiesė LN ir plokštumos ABD; lėktuvai LMN ir BDC .

2°) Įrodykite, kad trikampiai ABC ir LMN yra panašūs.

3) Sukonstruoti piramidės atkarpą pagal plokštumą AMN ; plokštuma LMN; lėktuvas LBC.

4*) Kuri iš piramidės atkarpų, einančių per viršūnę S, turi didžiausią plotą?

Tiesių ir plokštumų lygiagretumas

SABC tetraedre visi paviršiai yra taisyklingi trikampiai. Taškai L, M ir N yra atitinkamai kraštinių AS, BS, CS vidurio taškai. 1°) Nustatykite tiesių LM ir BC santykinę padėtį. 2°) Nustatykite tiesės LN ir plokštumos ABC santykinę padėtį.

3) Įrodykite, kad trikampiai LMN ir ABC yra panašūs.

Sukurkite kubo atkarpą, kuri yra: 1°) lygiakraštis trikampis; 2) penkiakampis.

217. Sukurkite tetraedro atkarpą, kuri yra lygiagretainis.

218°. Įrodykite, kad gretasienio priešingi paviršiai yra lygiagrečiai.

219. Įrodykite, kad visų tiesių, einančių per tam tikrą tašką ir lygiagrečių tam tikrai plokštumai, aibė sudaro lygiagrečią duotajai plokštumai.

220. Duoti keturi taškai A , B , C , D , esantys ne vienoje plokštumoje. Įrodykite, kad kiekviena plokštuma, lygiagreti tiesėms AB ir CD, lygiagretainio viršūnėse kerta tieses AC, AD, BD, BC.

221. Įrodykite, kad plokštuma ir šiai plokštumai nepriklausanti tiesė yra lygiagrečios viena kitai, jeigu jos abi lygiagrečios tai pačiai plokštumai.

222. Pro kubo ABCDA 1 B 1 C 1 D 1 įstrižainių susikirtimo tašką O nubrėžta plokštuma, lygiagreti su veidu ABCD. Ši plokštuma kerta briaunas BB 1 ir CC 1 atitinkamai taškuose M ir N. Įrodykite, kad kampas MON yra tiesus kampas.

223. Įrodykite, kad dvi plokštumos lygiagrečios viena kitai tada ir tik tada, kai kiekviena tiesė, kertanti vieną iš plokštumų, kerta kitą.

224*. Trikampėje piramidėje SABC per atkarpas AD ir CE, kur D yra SB vidurys, o E yra SA vidurys, nubrėžkite piramidės dalis lygiagrečiai viena kitai.

225. Raskite geometrines vietas:

1) visų atkarpų, kurių galai yra dviejose nurodytose lygiagrečiose plokštumose, vidurio taškai; 2*) atkarpų, kurių galai yra dviejose susikertančiose tiesėse, vidurio taškai.

226*. Plokštumoje α esančio trikampio ABC kraštinė AB lygiagreti plokštumai β. Lygiakraštis trikampis A 1 B 1 C 1 yra lygiagreti trikampio ABC projekcija į plokštumą β; AB = 5, BC = 6, AC = 9.

1) Nustatykite santykinę linijų AB ir A 1 B 1 padėtį,

BC ir B1 C1 , A1 C1 ir AC.

2) Raskite trikampio A 1 B 1 C 1 plotą.

227*. Duotos dvi susikertančios linijos. Nurodykite visų erdvės taškų aibę, per kurią galima nubrėžti liniją, kertančią kiekvieną iš dviejų nurodytų tiesių.

Pagrindinis apibrėžimas

Dvi plokštumos vadinamos

yra lygiagrečiai,

jei jie neturi bendrų taškų.

Pagrindiniai teiginiai

Lygiagretės ženklas Jei dvi vienos plokštumos plokštumos dviejų tiesių sankirtos yra atitinkamai lygiagrečios dviem antrosios plokštumos tiesėms, tai šios plokštumos

kaulai lygiagretūs.

Teorema apie ne- Jei dvi lygiagrečias dviejų lygiagrečių plokštumų sankirtas plokštuma kerta trečioji plokštuma, tai plokštumos trečiosios sankirtos tiesės

jie yra lygiagrečiai.

a α,b α,a ×b ,c β, d β, a || c , b || dα || β

α || β, a = γ∩α, b = γ∩β a || b

Mα

β: α || β, М β

Pasiruošimas teminiam

kam vertinimas tema "Tiesių ir plokštumų lygiagretumas"

Užduotys savikontrolei

1. Keturi taškai nepriklauso tai pačiai plokštumai. Ar gali kokie trys iš jų gulėti ant tos pačios linijos?

2. Ar gali trys skirtingos plokštumos turėti lygiai du bendrus taškus?

3. Ar dvi susikertančios tiesės vienu metu gali būti lygiagrečios trečiajai tiesei?

4. Ar tiesa, kad tiesiai a ir b nėra lygiagrečios, jei nėra tiesės c, lygiagrečios a ir b?

5. Ar vienodos atkarpos gali turėti nelygias projekcijas?

6. Ar spindulys gali būti lygiagreti linijos projekcija?

7. Ar kvadratas gali būti kubo atvaizdas?

8. Ar tiesa, kad per tam tikrą erdvės tašką gali būti tik viena plokštuma, lygiagreti tam tikrai tiesei?

9. Ar visada galima per tam tikrą tašką nubrėžti tiesę, lygiagrečią dviem nurodytoms plokštumoms, kuriose šio taško nėra?

10. Ar galima per dvi susikertančias tieses nubrėžti lygiagrečias plokštumas?

Atsakymai į savikontrolės užduotis

Bandomasis pavyzdys

Du lygiagretainiai АBCD ir АBC 1 D 1 yra skirtingose ​​plokštumose.

1°) Nustatykite tiesių CD ir C 1 D 1 santykinę padėtį.

2°) Nustatykite tiesės C 1 D 1 ir plokštumos santykinę padėtį

3°) Nubraižykite plokštumų DD 1 C 1 ir BCC 1 susikirtimo liniją.

4 °) Nustatykite santykinę plokštumų ADD 1 ir BCC 1 padėtį.

5) Per tašką M, dalijant atkarpą AB santykiu 2:1, skaičiuojant nuo taško A, nubrėžkite plokštumą α, lygiagrečią plokštumai C 1 BC. 6) Sukonstruoti tiesės AC susikirtimo tašką su plokštuma α ir rasti santykį, kuriuo šis taškas dalija atkarpą AC.

Abipusis tiesių ir plokštumų išdėstymas erdvėje

Trigonometrinis

Geometrijos pamokose jau nagrinėjote trigonometrines funkcijas. Iki šiol jų taikymas daugiausia apsiribojo trikampių sprendimu, tai yra, buvo siekiama rasti kai kuriuos trikampio elementus iš kitų. Iš matematikos istorijos žinoma, kad trigonometrijos atsiradimas yra susijęs su ilgių ir kampų matavimu. Tačiau dabar taikymo sritis

ją taikymo sritis yra daug platesnė nei senovėje.

Žodis „trigonometrija“ kilęs iš graikų kalbos τριγωνον

(trigononas) - trikampis ir µετρεω (metreo) - matuoju, keičiu

ryu. Pažodžiui tai reiškia trikampių matavimą.

AT Šiame skyriuje susisteminta jums jau žinoma medžiaga iš geometrijos kurso, tęsiamas trigonometrinių funkcijų tyrimas ir jų pritaikymas periodiniams procesams apibūdinti, ypač sukamajam judėjimui, virpesiams ir kt.

Dauguma trigonometrijos pritaikymų yra susiję būtent su periodiniais procesais, ty procesais, kurie kartojasi reguliariais intervalais. Saulės teka ir leidžiasi, metų laikų kaita, rato sukimasis – paprasčiausi tokių procesų pavyzdžiai. Mechaniniai ir elektromagnetiniai virpesiai taip pat yra svarbūs periodinių procesų pavyzdžiai. Todėl periodinių procesų tyrimas yra svarbi užduotis. O matematikos vaidmuo jos sprendime yra lemiamas.

ruošiamės studijuoti temą „Trigonometrinės funkcijos“

Pradėti nagrinėti temą „Trigonometrinės funkcijos“ patartina kartojant trikampių kampų trigonometrinių funkcijų apibrėžimus ir savybes bei jų taikymą sprendžiant tiek stačiakampius, tiek savavališkus trikampius.

Stačiakampio kampų sinusas, kosinusas, liestinė, kotangentas

trikampis

24 lentelė

Smagiojo kampo sinusas yra priešingos kojos ir hipotenuzės santykis:

sinα = a c .

Smailaus kampo kosinusas yra gretimos kojos ir hipotenuzės santykis:

cosα = b c .

Smailiojo kampo liestinė yra priešingos kojos ir gretimos kojos santykis:

tgα = a b .

Smailaus kampo kotangentas yra gretimos kojos ir priešingos kojos santykis:

ctga = a b .

Sinusas, kosinusas, liestinė, kampų nuo 0° iki 180° kotangentas

25 lentelė

sin α = R y ; cosα = R x ;

tgα = x y; ctgα = x y.

(X; adresu) – taško koordinatės BET esantis viršutiniame puslankiu, α - spindulio suformuotas kampas OA apskritimas su ašimi X.

Sinuso, kosinuso, liestinės, kotangentinės reikšmės

kai kurie kampai

26 lentelė

Kampas t

Savavališkų trikampių sprendimas

27 lentelė

Sinuso teorema

Trikampio kraštinės yra proporcingos priešingų kampų sinusams:

nuodėmė aα = nuodėmė bβ = nuodėmė cγ .

Kosinuso teorema

Savavališkos trikampio kraštinės kvadratas yra lygus kitų dviejų kraštinių kvadratų sumai, nepadvigubinant šių kraštinių sandaugos iš kampo tarp jų kosinuso:

c2 = a2 + b2 − 2 ab cos γ ,b2 = a2 + c2 − 2 ac cos β , a2 = b2 + c2 − 2 bc cos α .

Trikampio plotas yra pusė jo dviejų kraštinių ir kampo tarp jų sinuso sandaugos:

S= 1 2 abnuodėmėγ = 1 2 acnuodėmėβ = 1 2 bcnuodėmėα .

Pagrindinės trigonometrinės tapatybės

5. Palyginkite savavališko stačiakampio trikampio smailiųjų kampų sinusų sumą (žymime jąBET) su vienybe.

< 1. B.BET= 1.

> 1. G. Neįmanoma lyginti. Išdėstykite didėjančia tvarka: a= sin 30°, b= cos 30°,

= tg 30°.

< b< c. B.a< c< b. AT.c< a< b. G.b< a< c.

Palyginkite smailius kampus α ir β be skaičiavimo vidurkių, 7.

15. Nurodykite taško koordinatesBET gulėdami ant 1 spindulio apskritimo (žr. pav.).

(−1; 0). B.(1; 0).

(0; − 1). G.(0; 1).BET.AT.

Bet kurią technologinę operaciją galima atlikti tam tikru tikslumu, o tai reiškia, kad apdirbimo metu gautos detalės matmenys nebus idealūs, jie gali svyruoti tam tikrame diapazone. Norint įvykdyti surinkimo sąlygas ir užtikrinti patikimą detalės veikimą nurodytomis sąlygomis, būtina nustatyti leistiną intervalą, per kurį turi kristi galutinis dydis. Šiuo intervalu galima reguliuoti ne tik linijinius ar diametrinius matmenis, bet ir paviršių formą ar santykinę padėtį.

Formos ir vietos leistinus nuokrypius priskiria dizaineris, atsižvelgdamas į surinkimo sąlygas ir detalės ypatumus mechanizme.

Formos tolerancijos tipai

Formos tolerancija vadinama didžiausia leistina formos nuokrypio reikšme.

Formos tolerancijos laukas- tai plotas plokštumoje arba erdvėje, kurio viduje visi nagrinėjamo elemento taškai turi būti normalizuotoje srityje, kurios plotis arba skersmuo nustatomas pagal tolerancijos vertę, o vieta tikrojo elemento atžvilgiu gretimu elementu.

Formos nuokrypiai ir tolerancijos

Yra šie formos nukrypimų nuokrypiai:

• Nukrypimas nuo tiesumo plokštumoje
• išgaubtas
• įdubimas
• Nukrypimas nuo lygumo ir plokštumo tolerancija
• Išgaubtas
• Įdubimas
• Apvalumo nuokrypis ir apvalumo tolerancija
• ovalumas
• Iškirpti
• Cilindriškumo nuokrypis ir cilindriškumo tolerancija
• Cilindrinio paviršiaus išilginio pjūvio profilio nuokrypis ir tolerancija
• Išilginio pjūvio profilio nuokrypis
• smailėjantis
• statinės forma
• balno forma

Leistini nukrypimai žymimi specialiais simboliais.

Vietos tolerancijos tipai

Vietos tolerancija- riba, kuri riboja leistiną vietos nuokrypio reikšmę.

Yra vietos ir orientacijos tolerancijos.

Vietos tolerancijos laukas- plotas plokštumoje arba erdvėje, kurio viduje turi būti gretimas elementas arba simetrijos plokštuma, ašis, centras normalizuotoje srityje, kurio skersmuo arba plotis nustatomas pagal tolerancijos vertę, ir santykinis padėtis nustatoma pagal nominalią atitinkamo elemento vietą.

Nukrypimai ir vietos tolerancijos

Yra šie vietos tolerancijos tipai:

• Paralelizmo nuokrypis ir paralelizmo tolerancija
• Nuokrypio ir statmenumo tolerancija
• Nuokrypio ir posvyrio tolerancija
• Nuokrypio ir išlyginimo tolerancija
• Spindulio tolerancija
• Nuokrypių ir simetrijos tolerancija
• Padėties nuokrypis ir padėties tolerancija
• Tolerancija diametrine prasme
• Spindulio tolerancija
• Nukrypimas nuo susikirtimo ir ašių susikirtimo tolerancija
• Tolerancija diametrine prasme
• Spindulio tolerancija

Bendros tolerancijos

Yra keletas bendros formos ir vietos tolerancijos tipų.

• Radialinis išbėgimas
• Pilnas radialinis išleidimas
• Veido išsekimas
• Pilnas ašinis išleidimas
• Bėgimas tam tikra kryptimi
• Tam tikro profilio formos nuokrypis ir tolerancija
• Tam tikro paviršiaus formos nuokrypis ir tolerancija

Šie leistini nuokrypiai pažymėti simboliais.

Formos ir vietos leistinų nuokrypių žymėjimas brėžiniuose

Formos ir vietos leistinos nuokrypos brėžiniuose pavaizduotos rėmo pavidalu, kuris yra padalintas į keletą dalių. Pirmoje dalyje pavaizduotas grafinis tolerancijos žymėjimas, antroje dalyje - skaitinė tolerancijos reikšmė, trečioje ir vėlesnėje - vienos ar kelių bazių žymėjimas raidėmis.

Jei tolerancijos pagrindo nėra, rėmas susideda tik iš dviejų dalių. Formos ir vietos tolerancijos rėmų pavyzdžiai pateikti paveikslėlyje.

Paveikslėlyje kairėje pavaizduotas rėmas su formos tolerancija (leistinas nuokrypis nuo tiesumo), dešinėje su vietos tolerancija (leistinas nukrypimas nuo lygiagretumo).

Rėmas pagamintas plonomis linijomis. Teksto aukštis rėmelyje turi būti lygus matmenų skaičių šrifto dydžiui. Nuo tolerancijos rėmelio iki paviršiaus arba iki lyderio nubrėžiama linija, kuri baigiasi rodykle.

Prieš skaitinę tolerancijos reikšmę galima nurodyti ženklus:

• f - jei cilindrinis arba apskritas tolerancijos laukas nurodomas skersmeniu
• R – jei cilindrinis arba apskritas laukas pažymėtas spinduliu
• T - jei ašių susikirtimo tolerancijos laukas, simetrija, yra apribotas dviem lygiagrečiomis tiesėmis arba plokštumomis diametrine prasme.
• T / 2 - tuo pačiu atveju kaip T, tik spindulio išraiška
• Sfera – sferiniam tolerancijos laukui.

Jei tolerancija turėtų būti taikoma ne visam paviršiui, o tik tam tikram plotui, tada tai nurodoma brūkšneliu su punktyrine linija.

Vienam elementui gali būti nurodytos kelios leistinos nuokrypos, šiuo atveju rėmeliai brėžiami vienas virš kito.

Virš arba po rėmeliu gali būti rodoma papildoma informacija.

Informaciją apie formą ir vietą galima nurodyti .

Nenurodytos išlygiavimo tolerancijos pagal GOST 25069-81.

Priklausomos tolerancijos

Priklausomos vietos tolerancijos pažymėtos tokiu simboliu.

Šis simbolis gali būti dedamas po skaitinės tolerancijos vertės, jei priklausomas nuokrypis yra susijęs su faktiniais atitinkamo elemento matmenimis. Taip pat simbolis gali būti dedamas po raidės žymėjimo (jei jo nėra, tada trečiajame rėmelio lauke), jei priklausoma nuokrypa yra susijusi su faktiniais pagrindinio elemento matmenimis.

Priskirkite formos ir vietos nuokrypius

Kuo detaliau bus pagaminta tiksliau, tuo tikslesnių įrankių reikės jos gamybai ir matmenų kontrolei. Tai automatiškai padidins jo vertę. Pasirodo, detalės gamybos kaina labai priklauso nuo reikalaujamo tikslumo ją gaminant. Tai reiškia, kad projektuotojas turi nurodyti tik tuos leistinus nuokrypius, kurie tikrai būtini judesio surinkimui ir patikimam veikimui. Leistini intervalai taip pat turėtų būti priskirti atsižvelgiant į surinkimo ir atlikimo sąlygas.

Formos tolerancijos skaitinės reikšmės

Priklausomai nuo tikslumo klasės, nustatomos standartinės formos leistinų nuokrypių reikšmės.

Plokštumo ir tiesumo tolerancijos

Šiuo atveju vardinis dydis laikomas normalizuotos sekcijos vardiniu ilgiu.

Apvalumo, cilindriškumo, išilginio profilio leistinos nuokrypos

Šie leistini nuokrypiai priskiriami tais atvejais, kai jie turi būti mažesni už dydžio leistiną nuokrypį.

Nominalus dydis yra vardinis paviršiaus skersmuo.

Statmens, lygiagretumo, nuolydžio, ašinio išbėgimo tolerancijos

Nominalus dydis priskiriant lygiagretumo, statmenumo, nuolydžio leistinus nuokrypius suprantamas kaip vardinis normalizuotas pjūvis arba viso valdomo paviršiaus vardinis ilgis.

Radialinio išsiveržimo, simetrijos, ašių sankirtos koaksialumo tolerancijos diametrais

Priskiriant radialines nuotėkio leistinas nuokrypas, vardinis dydis laikomas atitinkamo paviršiaus vardiniu skersmeniu.

Priskiriant simetrijos, išlygiavimo ašies susikirtimo nuokrypius, vardinis dydis yra nominalus paviršiaus skersmuo arba vardinis dydis tarp paviršių, sudarančių atitinkamą elementą.

Kiekvienas, kuris kada nors mokėsi ar šiuo metu studijuoja mokykloje, turėjo susidurti su įvairiais sunkumais studijuodamas disciplinas, kurios yra įtrauktos į Švietimo ministerijos parengtą programą.

Su kokiais sunkumais susiduriate

Kalbų studijas lydi esamų gramatikos taisyklių ir pagrindinių jų išimčių įsiminimas. Kūno kultūra reikalauja iš mokinių puikaus skaičiavimo, geros fizinės formos ir didelės kantrybės.

Tačiau niekas neprilygsta sunkumams, kylantiems studijuojant tikslias disciplinas. Algebra, kurioje yra sudėtingų elementarių problemų sprendimo būdų. Fizika su gausiu fizikinių dėsnių formulių rinkiniu. Geometrija ir jos skyriai, pagrįsti sudėtingomis teoremomis ir aksiomomis.

Pavyzdys yra aksiomos, paaiškinančios plokštumų lygiagretumo teoriją, kurią reikia atsiminti, nes jomis grindžiamas visas stereometrijos mokyklos mokymo programos kursas. Pabandykime išsiaiškinti, kaip lengviau ir greičiau tai padaryti.

Lygiagrečios plokštumos pagal pavyzdžius

Aksioma, nurodanti plokštumų lygiagretumą, yra tokia: " Bet kurios dvi plokštumos laikomos lygiagrečiomis tik tuo atveju, jei jose nėra bendrų taškų.“, tai yra, jie nesikerta vienas su kitu. Norėdami įsivaizduoti šį paveikslą išsamiau, kaip elementarų pavyzdį galime pateikti pastato lubų ir grindų arba priešingų sienų santykį. Iš karto tampa aišku, kas turima galvoje, taip pat patvirtinamas faktas, kad šios plokštumos įprastu atveju niekada nesusikirs.

Kitas pavyzdys – dvigubo stiklo langas, kur stiklo lakštai veikia kaip plokštumos. Jie taip pat jokiomis aplinkybėmis nesudarys susikirtimo taškų. Be to, galite pridėti knygų lentynų, Rubiko kubą, kuriame plokštumos yra priešingi jo veidai, ir kitų kasdienio gyvenimo elementų.

Nagrinėjamos plokštumos žymimos specialiu ženklu dviejų tiesių „||“ pavidalu, aiškiai iliustruojančių plokštumų lygiagretumą. Taigi, taikant realius pavyzdžius, galima susidaryti aiškesnį temos suvokimą, todėl toliau galima pereiti prie sudėtingesnių sąvokų svarstymo.

Kur ir kaip taikoma lygiagrečių plokštumų teorija?

Studijuodami mokyklinį geometrijos kursą, studentams tenka spręsti įvairiapuses užduotis, kur dažnai reikia nustatyti tiesių lygiagretumą, tiesę ir plokštumą tarpusavyje arba plokštumų priklausomybę viena nuo kitos. Analizuojant esamą būklę, kiekviena užduotis gali būti susieta su keturiomis pagrindinėmis stereometrijos klasėmis.

Pirmoji klasė apima užduotis, kuriose reikia nustatyti tiesės ir plokštumos lygiagretumą tarpusavyje. Jo sprendimas redukuojamas iki to paties pavadinimo teoremos įrodymo. Norėdami tai padaryti, turite nustatyti, ar tiesei, kuri nepriklauso nagrinėjamai plokštumai, šioje plokštumoje yra lygiagreti linija.

Antroji uždavinių klasė apima tuos, kuriuose naudojamas lygiagrečių plokštumų ženklas. Jis naudojamas siekiant supaprastinti įrodinėjimo procesą ir taip žymiai sutrumpinti sprendimo paieškos laiką.

Kita klasė apima problemų, susijusių su tiesių atitikimu pagrindinėms plokštumų lygiagretumo savybėms, spektrą. Ketvirtosios klasės uždavinių sprendimas – nustatyti, ar tenkinama lygiagrečių plokštumų sąlyga. Tiksliai žinant, kaip vyksta konkrečios problemos įrodinėjimas, studentams tampa lengviau orientuotis taikant esamą geometrinių aksiomų arsenalą.

Taigi užduotys, kurių sąlyga reikalauja nustatyti ir įrodyti tiesių, tiesės ir plokštumos arba dviejų plokštumų lygiagretumą tarpusavyje, redukuojami iki teisingo teoremos parinkimo ir sprendimo pagal esamą aibę. taisykles.

Apie tiesės ir plokštumos lygiagretumą

Tiesės ir plokštumos lygiagretumas yra ypatinga stereometrijos tema, nes būtent tai yra pagrindinė koncepcija, kuria grindžiamos visos tolesnės geometrinių figūrų lygiagretumo savybės.

Pagal turimas aksiomas tuo atveju, kai du tiesės taškai priklauso tam tikrai plokštumai, galime daryti išvadą, kad joje yra ir duotoji tiesė. Esant tokiai situacijai, tampa aišku, kad yra trys linijos vietos, palyginti su plokštuma erdvėje, parinktys:

1. Linija priklauso plokštumai.
2. Tiesei ir plokštumai yra vienas bendras susikirtimo taškas.
3. Tiesės ir plokštumos susikirtimo taškų nėra.

Mus ypač domina paskutinis variantas, kai nėra susikirtimo taškų. Tik tada galime pasakyti, kad tiesė ir plokštuma yra lygiagrečios viena kitos atžvilgiu. Taigi patvirtinama pagrindinės teoremos sąlyga tiesės ir plokštumos lygiagretumo ženklu, kuri teigia, kad: "Jei tiesė, nepriklausanti aptariamai plokštumai, yra lygiagreti bet kuriai tos plokštumos tiesei, tai aptariama linija taip pat yra lygiagreti nurodytai plokštumai."

Būtinybė naudoti paralelizmo ženklą

Plokštumų lygiagretumo ženklas dažniausiai naudojamas ieškant supaprastinto plokštumų uždavinių sprendimo. Šio ženklo esmė yra tokia: Jei yra dvi susikertančios tiesės, esančios toje pačioje plokštumoje, lygiagrečios dviem kitai plokštumai priklausančioms tiesėms, tada tokias plokštumas galima vadinti lygiagrečiomis».

Papildomos teoremos

Be plokštumų lygiagretumą įrodančio požymio naudojimo, praktiškai galima susidurti su dar dviejų papildomų teoremų naudojimu. Pirmasis pateikiamas tokia forma: Jei viena iš dviejų lygiagrečių plokštumų yra lygiagreti trečiajai, tai antroji plokštuma taip pat yra lygiagreti trečiajai arba visiškai su ja sutampa».

Remiantis pateiktų teoremų vartojimu, visada galima įrodyti plokštumų lygiagretumą nagrinėjamos erdvės atžvilgiu. Antroji teorema parodo plokštumų priklausomybę nuo statmenos linijos ir turi tokią formą: Jei dvi nesutampančios plokštumos yra statmenos kokiai nors tiesei, tai jos laikomos lygiagrečios viena kitai».

Būtinosios ir pakankamos sąlygos samprata

Pakartotinai sprendžiant plokštumų lygiagretumo įrodinėjimo uždavinius, buvo išvesta būtina ir pakankama plokštumų lygiagretumo sąlyga. Žinoma, kad bet kuri plokštuma pateikiama parametrine lygtimi, kurios forma: A 1 x+ B 1 y+ C 1 z+D 1 =0. Mūsų sąlyga yra pagrįsta lygčių sistemos, nurodančios plokštumų vietą erdvėje, naudojimu ir yra pavaizduota tokia formuluote: Norint įrodyti dviejų plokštumų lygiagretumą, būtina ir pakanka, kad lygčių sistema, apibūdinanti šias plokštumas, būtų nenuosekli, tai yra, neturėtų sprendinio».

Pagrindinės savybės

Tačiau sprendžiant geometrinius uždavinius ne visada pakanka naudoti paralelizmo ženklą. Kartais susidaro situacija, kai reikia įrodyti dviejų ar daugiau tiesių skirtingose ​​plokštumose lygiagretumą arba šiose tiesėse esančių atkarpų lygybę. Norėdami tai padaryti, naudokite lygiagrečių plokštumų savybes. Geometrijoje jų yra tik du.

Pirmoji savybė leidžia spręsti apie linijų lygiagretumą tam tikrose plokštumose ir pateikiama tokia forma: Jei dvi lygiagrečias plokštumas kerta trečioji, tada susikirtimo tiesių sudarytos linijos taip pat bus lygiagrečios viena kitai».

Antrosios savybės prasmė yra įrodyti lygiagrečiose tiesėse esančių atkarpų lygybę. Jo aiškinimas pateikiamas žemiau. “ Jei atsižvelgsime į dvi lygiagrečias plokštumas ir tarp jų įtrauksime sritį, tada galima teigti, kad šios srities suformuotų atkarpų ilgis bus toks pat».