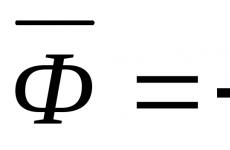Принцип даламбера для материальной точки гласит. Аналитическая механика материальной точки и динамика твердого тела эйлера. Принцип даламбера для механическойй системы. Главный вектор и главный момент сил инерции

Принцип Даламбера

Основной труд Ж.Л. Даламбера (1717-1783) - "Трактат о динамике» - была опубликована в 1743

Первая часть трактата посвящена построению аналитической статики. Здесь Даламбер формулирует "основные принципы механики", среди которых "принцип инерции", "принцип добавления движений" и "принцип равновесия".

"Принцип инерции" сформулирован отдельно для случая покоя и для случая равномерного прямолинейного движения. "Силой инерции, - пишет Даламбер, т я вместе с Ньютоном называю свойство тела сохранять то состояние, в котором оно находится".

"Принцип добавления движений" представляет собой закон сложения скоростей и сил по правилу параллелограмма. На основе этого принципа Даламбер решает задачи статики.

"Принцип равновесия" сформулировано в виде следующей теоремы: "Если два тела движущихся со скоростями, обратнопропорциональна их массам, имеют противоположные направления, так что одно тело не может двигаться, не сдвигая с места на другое тело, то эти тела будут находиться в состоянии равновесия" . Во второй части «Трактата» Даламбер предложил общий метод составления дифференциальных уравнений движения любых материальных систем, основанный на сведении задачи динамики к статике. Он сформулировал правило для любой системы материальных точек, названное впоследствии "принципом Даламбера", согласно которому приложены к точкам системы силы можно разложить на "действующие", то есть такие, которые вызывают ускорение системы, и "потерянные", необходимые для равновесия системы. Даламбер считает, что силы, которые соответствуют "потерянным" ускорением, образуют такую совокупность, которая никак не влияет на фактическое поведение системы. Иными словами, если к системе приложить только совокупность "потерянных" сил, то система останется в покое. Современная формулировка принципа Даламбера дал М Е. Жуковский в своем "Курсе теоретической механики": "Если в какой-либо момент времени остановить систему, движется, и добавить к ней, кроме ее движущих сил, еще все силы инерции, соответствующие данному моменту времени, то будет наблюдаться равновесие, при этом все силы давления, натяжения и т.д. развивающихся между частями системы при такой равновесии, будут настоящими силами давления, натяжения и т.д. при движении системы в рассматриваемый момент времени ". Следует отметить, что сам Даламбер при изложении своего принципа не прибегал ни к понятию силы (считая, что оно не является достаточно четким, чтобы входить в перечень основных понятий механики), ни тем более к понятию силы инерции. Изложение принципа Даламбера с применением термина "сила" принадлежит Лагранжа, который в своей "Аналитической механике» дал его аналитическое выражение в форме принципа возможных перемещений. Именно Жозеф Луи Лагранж (1736-1813) и особенно Леонардо Эйлер (1707-1783) видиигралы существенную роль в окончательном превращении механики на аналитическую механику.

Аналитическая механика материальной точки и динамика твердого тела Эйлера

Леонардо Эйлер - один из выдающихся ученых, который внес большой вклад в развитие физико-математических наук в XVIII в. Его творчество поражает проницательностью исследовательской мысли, универсальностью дарования и огромным объемом оставленной научного наследия.

Уже в первые годы научной деятельности в Петербурге (Эйлер приехал в Россию в 1727 г..) Он составил программу грандиозного и всеобъемлющего цикла работ в области механики. Это приложение находится в его двухтомном труде "Механика или наука о движении, изложенная аналитически" (1736). "Механика" Эйлера была первым систематическим курсом ньютоновской механики. Она содержала основы динамики точки - под механикой Эйлер понимал наукучхро движение, в отличие от науки о равновесии сил, или статики. Определяющей чертой "Механики" Эйлера было широкое использование нового математического аппарата - диференциальнотвчй интегрального исчислений. Коротко охарактеризовав основные труды по механике, появившиеся на рубеже XVII-XVIII вв., Эйлер отмечал сын-тетико-геометрический стиль их викладу.що создавал для читателей очень много труда. Именно в такой манере написаны "Начала" Ньютона и более поздняя "Фо-рономия" (1 716) Я. Германа. Эйлер указывает, что работы Германа и Ньютона изложенные "по обычаю древних с помощью синтетических геометрических доказательств" без применения анализа, "только благодаря которому и можно достичь полного понимания этих вещей".

Синтетика-геометрический метод не имел обобщающего характера, а требовал, как правило, индивидуальных построений относительно каждой задачи в отдельности. Эйлер признается, что после изучения "Форономии" и "Начал" он, как ему казалось, "достаточно ясно понял решения многих задач, однако задач, какой-то мере отступают от них, уже решить не мог". Тогда он попытался "выделить анализ по этому синтетического метода и те же предложения для собственной пользы проделать аналитически". Эйлер отмечает, что благодаря этому он значительно лучше понял суть вопроса. Он разработал принципиально новые методы исследования проблем механики, создал ее математический аппарат и блестяще применил его ко многим сложных задач. Благодаря Эйлеру дифференциальная геометрия, дифференциальные уравнения, вариационное исчисление стали инструментом механики. Метод Эйлера, развитый позднее его преемниками, был однозначным и адекватным предмету.

Работа Эйлера по динамике твердого тела "Теория движения твердых тел" имеет большой вступление из шести разделов, где снова изложены динамику точки. В вступление внесен ряд изменений: в частности, уравнения движения точки записываются с помощью проектирования на оси неподвижных прямоугольных координат (а не на касательную, главную нормаль и нормаль, то есть оси недвижимого природного трехгранника, связанного с точками траектории, как в "Механике") .

Следующий после вступления «Трактат о движении твердых тел" состоит из 19 разделов. В основу трактата положен принцип Даламбера. Коротко остановившись на поступательном движении твердого тела и введя понятие центра инерции, Эйлер рассматривает вращения вокруг неподвижной оси и вокруг неподвижной точки. Здесь представлены формулы для проекций мгновенной угловой скорости, углового ускорения на оси координат, используются так называемые углы Эйлера и т.д. Далее изложены свойства момента инерции, после чего Эйлер переходит собственно к динамике твердого тела. Он выводит дифференциальные уравнения вращения тяжелого тела вокруг его недвижимого центра тяжести при отсутствии, внешних сил и решает их для простого частного случая. Так возникла известная и столь же важна в теории гироскопа задача о вращении твердого тела вокруг неподвижной точки. Эйлер работал также над теорией судостроения, в глазах гидро- и аэромеханики, баллистики, теории устойчивости и теории малых колебаний, небесной механики и др.

Через восемь лет после выхода "Механики" Эйлер обогатил науку первым точной формулировкой принципа наименьшего действия. Формулировка принципа наименьшего действия, которые принадлежали Мопертюи, были еще очень несовершенны. Первое научное формулировка принципа принадлежит Эйлеру. Он сформулировал свой принцип следующим образом: интеграл имеет наименьшее значение для настоящей траектории, если рассматривать

последнюю в группе возможных траекторий, имеющих общие начальное и конечное положение и осуществляются с тем же значением энергии. Эйлер предоставляет своему принципу точного математического выражения и строгого обоснования для одной материальной точки, испытывает действия центральных сил. В течение 1746-1749 pp. Эйлер написал несколько работ о фигурах равновесия гибкой нити, где принцип наименьшего действия были применены к задачам, в которых действуют упругие силы.

Таким образом, к 1744 механика обогатилась двумя важными принципами: принципом Даламбера и принципу наименьшего действия Мопертюи-Эйлера. Опираясь на эти принципы, Лагранж построил систему аналитической механики.

Принцип Даламбера устанавливает единый подход к исследованию движения материального объекта вне зависимости от характера налагаемых на это движение условий. При этом динамическим уравнениям движения придается вид уравнений равновесия. Отсюда второе название принципа Даламбера – метод кинетостатики.

Для материальной точки в любой момент движения геометрическая сумма приложенных активных сил, реакций связей и условно присоединенной силы инерции равна нулю (рис. 48).

Где Ф-сила инерции материальной точки, равная:

. (15.2)

Рисунок 48

Рисунок 49

16. Принцип даламбера для механическойй системы. Главный вектор и главный момент сил инерции.

Если к каждой точке механической системы в любой момент движения условно приложить соответствующую силы инерции, то в любой момент движения геометрическая сумма действующих на точку активных сил, реакций связей и силы инерции равна нулю.

Уравнение, выражающее принцип Даламбера для механической системы, имеет вид
. (16.1) Сумма моментов этих уравновешенных сил относительно любого центра также равна нулю
. (16.2) При применении принципа Даламбера уравнения движения системы составляются в форме уравнений равновесия. С помощью уравнений (16.1) и (16.2) можно определить динамические реакции.

ПРИМЕР 22.

Вертикальный вал АК, вращающийся с постоянной угловой скоростью =10с -1 , закреплен подпятником в точке А и цилиндрическим подшипником в точке К (рис. 52). К валу в точке Е прикреплены тонкий однородный ломаный стержень массой m=10кг и длиной 10b, состоящий из частей 1 и 2, где b=0,1м, а их массы m 1 и m 2 пропорциональны длинам. Стержень прикреплен к валу шарниром в точке Е и невесомым стержнем 4 жестко закрепленным в точке В. Определить реакцию шарнира Е и стержня 4.

РЕШЕНИЕ.

1. Длина ломаного стержня равна 10b. Выразим массы частей стержня, пропорциональные длинам: m 1 =0,4m; m 2 =0,3m; m 3 =0,3m.

Рисунок 42

Если тело имеет плоскость симметрии и вращается вокруг неподвижной оси z, перпендикулярной плоскости симметрии и не проходящей через центр масс тела, сила инерции всех точек тела приводится к равнодействующей, равной главному вектору сил инерции системы, но приложенной к некоторой точке К (рис. 54). Линия действия равнодействующей отстоит от точки О на расстоянии
. (16.10)

При плоском движении тела, имеющего плоскость симметрии, тело движется вдоль этой плоскости (рис.55). Главный вектор и главный момент сил инерции также лежат в этой плоскости и определяются по формулам:

Рисунок 55

.

Знак минус показывает, что направление момента
противоположно направлению углового ускорения тела.

ПРИМЕР 23.

Определить силу, стремящуюся разорвать равномерно вращающийся маховик массой m, считая его массу распределенной по ободу. Радиус маховика r, угловая скорость (рис. 56).

РЕШЕНИЕ.

1. Искомая сила является внутренней.-- равнодействующая сил инерции элементов обода.
. Выразим координату х с центра масс дуги обода с центральным углом
:
, тогда
.

2. Для определения силы применим принцип Даламбера в проекции на ось х:
;
, откуда
.

3. Если маховик – сплошной однородный диск, то
, тогда
.

Просмотр: эта статья прочитана 44027 раз

Pdf Выберите язык... Русский Украинский Английский

Краткий обзор

Полностью материал скачивается выше, предварительно выбрав язык

Общие принципы динамики

Принцип Германа - Эйлера - Даламбера

Сила инерции

Принцип Даламбера (принцип кинетостатики) является одним из общих принципов механики, с помощью которого уравнениям динамики по форме придается вид уравнений статики. Принцип был предложен Германом в 1716 году, обобщен Эйлером в 1737 году.

Материальная точка М движется с ускорением под действием приложенных сил. Третий закон динамики отображает двусторонность механических процессов природы. При взаимодействии двух тел приложенные к каждому из них силы равны по модулю и направлены противоположно. Так как эти силы приложены к разным телам, они не уравновешиваются. Например, при взаимодействия некоторого тела А и точки М , которая имеет массу m , точка получает ускорение. Тело А действует на точку М с силой F=-ma . По закону действия и противодействия материальное точка М действует на тело А с силой Ф=-F=-ma , которая называется силой инерции.

Сила инерции или сила Даламбера - векторная величина, имеющая размерность силы, по модулю равна произведению массы точки на ее ускорение, и направлена противоположно этому ускорению.

Принцип Даламбера для материальной точки

Если в любой момент времени к фактически действующим на материальную точку силам добавить силу инерции, то полученная система сил будет уравновешенной.

Это означает, что для решения задачи динамики по принципу Германа - Эйлера - Даламбера следует, помимо приложенных к точке сил, условно приложить к этой точке силу инерции. приложение силы инерции к точке является условным приемом, сводящим задачу динамики лишь по форме решения к задаче статики.

Принцип Даламбера для системы материальных точек

Если в любой момент времени к каждой из точек системы, кроме фактически действующих на нее внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и для нее можно будет применить все уравнения статики.

Принцип Даламбера для несвободной механической системы

В любой момент времени для каждой точки несвободной механической системы, кроме фактически действующих на нее сил, добавить соответствующие силы инерции, то полученная система сил будет уравновешенной и для нее можно будет применить все уравнения статики.

То есть, в любой момент времени для каждой точки несвободной механической системы геометрическая сумма главных векторов заданных сил, реакций опор и сил инерции материальных точек системы равна нулю.

В любой момент времени для любой точки несвободной механической системы геометрическая сумма главных моментов заданных сил, реакций опор и сил инерции материальных точек системы относительно любого неподвижного центра равна нулю.

Обобщенная форма уравнений равновесия по принципу Даламбера

Приведение сил инерции точек твердого тела к простейшему виду.

Случаи приведения системы сил инерции твердого тела простейшему виду.

Поступательное движение

При поступательном движении силы инерции твердого тела приводятся до одной равнодействующей, проходящей через центр масс тела, и равной по модулю произведению массы тела на модуль ускорения его центра масс и направленной противоположно этому ускорению.

Вращения вокруг центра масс нет, поэтому момент силы инерции равен нулю.

Вращательное движение тела вокруг оси, проходящей через центр масс тела.

Если тело вращается вокруг неподвижной оси проходящей через центр масс тела, то силы инерции приводятся к одной паре сил, лежащей в плоскости перпендикулярной оси вращения.

Поскольку центр масс не движется главный вектор сил инерции равен нулю.

Плоскопаралельний движение

При плоском движении тела система сил инерции приводится к силе, приложенной в центре масс тела и паре сил. Направление момента силы инерции противоположен угловому ускорению тела.

Принцип возможных перемещений

Принцип возможных перемещений в общем виде определяет условия равновесия любой механической системы, то есть позволяет решать задачи статики, как задачи динамики.

Перемещение точек несвободной механической системы ограничено имеющимися связями. Положение точек системы определяется заданием независимых координат.

Независимые величины, заданием которых можно однозначно определяется положение всех точек механической системы, называются обобщенными координатами этой системы. Как правило, число обобщенных координат механической системы равно числу степеней свободы этой системы. Например, положение всех точек кривошипно-шатунного механизма определяется заданием угла поворота кривошипа.

Возможные или виртуальные перемещения

Возможные или виртуальные перемещения системы - это воображаемые бесконечно малые перемещения точек системы, допускаемые в данный момент наложенными на систему связями.

Криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательной к траекториям точек.

Число независимых между собой возможных перемещений системы называется числом степеней свободы этой системы.

Возможная или виртуальная работа

Возможная (или виртуальная) работа − это элементарная работа, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки.

Принцип возможных перемещений для механической системы

Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма робот всех активных сил при любом возможном перемещении системы равнялась нулю.

Уравнение возможных работ − математическое выражение необходимого и достаточного условий равновесия любой механической системы.

Общее уравнение динамики

Общее уравнение динамики (принцип Даламбера - Лагранжа)

Принцип возможных перемещений, дающий общий метод решения задач статики, можно применить и к решению задач динамики. На основании принципа Германа—Эйлера—Даламбера для несвободной механической системы в любой момент времени геометрическая сумма равнодействующей задаваемых сил, равнодействующей реакций связей и силы инерции для каждой точки Mn механической системы равна нулю.

Если система получает возможное перемещение, при котором каждая точка имеет возможное перемещение, то сумма работ этих сил на перемещении должна быть равна нулю.

Общее уравнение динамики для системы с идеальными связями

Положим, что все связи в рассматриваемой механической системе двусторонние и идеальные (силы трения, если они имеются, отнесены к числу задаваемых сил). Тогда сумма работ реакций связей на возможных перемещениях системы равна нулю.

При движении механической системы с идеальными связями в любой данный момент времени сумма элементарных робот всех активных (заданных) сил и всех сил инерции на любом возможном перемещении системы равняется нулю.

Общие уравнения динамики позволяют составить дифференциальные уравнения движения любой механической системы. Если механическая система состоит из отдельных твердых тел, то силы инерции точек каждого тела можно привести к силе, приложенной в некоторой точке тела, и паре сил. Сила равна главному вектору сил инерции точек этого тела, а момент пары равен главному моменту этих сил относительно центра приведения. Чтобы воспользоваться принципом возможных перемещений, к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силу и пару, составленные силами инерции точек тела. Затем системе сообщают возможное перемещение и для всей совокупности задаваемых сил и приведенных сил инерции составляют общее уравнение динамики

Формат: pdf

Размер: 600КВ

Язык: русский, украинский

Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.

Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.

Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается

Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается

Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы

Принцип Даламбера позволяет сформулировать задачи динамики механических систем как задачи статики. При этом динамическим дифференциальным уравнениям движения придают вид уравнений равновесия. Такой метод называют методом кинетостатики .

Принцип Даламбера для материальной точки: «В каждый момент времени движения материальной точки, фактически действующие на нее активные силы, реакции связей и условно приложенная к точке сила инерции образуют уравновешенную систему сил »

Силой инерции точки называют векторную величину, имеющую размерность силы, равную по модулю произведению массы точки на ее ускорение и направленную противоположно вектору ускорения

. (3.38)

Рассматривая механическую систему как совокупность материальных точек, на каждую из которых действуют, согласно принципу Даламбера, уравновешенные системы сил, имеем следствия из этого принципа применительно к системе. Главный вектор и главный момент относительно любого центра приложенных к системе внешних сил и сил инерции всех ее точек равны нулю:

(3.39)

Здесь внешними силами являются активные силы и реакции связей.

Главный вектор сил инерции механической системы равен произведению массы системы на ускорение ее центра масс и направлен в сторону, противоположную этому ускорению

. (3.40)

Главный момент сил инерции системы относительно произвольного центра О равен взятой с обратным знаком производной по времени от кинетического момента ее относительно того же центра

. (3.41)

Для твердого тела, вращающегося вокруг неподвижной оси Oz , найдем главный момент сил инерции относительно этой оси

. (3.42)

3.8. Элементы аналитической механики

В разделе «Аналитическая механика» рассматривают общие принципы и аналитические методы решения задач механики материальных систем.

3.8.1.Возможные перемещения системы. Классификация

некоторых связей

Возможными перемещениями точек
механической системы называют любые воображаемые, бесконечно малые их перемещения, допускаемые наложенными на систему связями, в фиксированный момент времени. По определению, числом степеней свободы механической системы называют число ее независимых возможных перемещений.

Связи, наложенные на систему, называют идеальными , если сумма элементарных работ их реакций на любом из возможных перемещений точек системы равна нулю

. (3. 43)

Связи, для которых налагаемые ими ограничения сохраняются при любом положении системы, называют удерживающими . Связи, не изменяющиеся во времени, в уравнения которых явно не входит время, называют стационарными . Связи, ограничивающие только перемещения точек системы, называют геометрическими , а ограничивающие скорости – кинематическими . В дальнейшем будем рассматривать только геометрические связи и те кинематические, которые могут быть путем интегрирования сведены к геометрическим.

3.8.2. Принцип возможных перемещений

Для равновесия механической системы с удерживающими идеальными и стационарными связями необходимо и достаточно, чтобы

сумма элементарных работ всех активных сил, действующих на нее, на любых возможных перемещениях системы была равна нулю

. (3.44)

В проекциях на оси координат:

. (3.45)

Принцип возможных перемещений позволяет установить в общей форме условия равновесия любой механической системы, не рассматривая равновесие отдельных ее частей. При этом учитываются только действующие на систему активные силы. Неизвестные реакции идеальных связей в эти условия не входят. Вместе с тем данный принцип позволяет определять неизвестные реакции идеальных связей путем отбрасывания этих связей и введения их реакций в число активных сил. При отбрасывании связей, реакции которых необходимо определить, система приобретает дополнительно соответствующее число степеней свободы.

Пример 1 . Найти зависимость между силами идомкрата, если известно, что при каждом повороте рукояткиАВ = l , винт С выдвигается на величину h (рис. 3.3).

Решение

Возможные перемещения механизма – это поворот рукоятки  и перемещение груза h . Условие равенства нулю элементарных работ сил:

Pl  – Q h = 0;

Тогда
. Так какh  0, то

3.8.3. Общее вариационное уравнение динамики

Рассмотрим движение системы, состоящей из n точек. На нее действуют активные силы и реакции связей .(k = 1,…,n ) Если к действующим силам добавить силы инерции точек
, то, согласно принципу Даламбера, полученная система сил будет находиться в равновесии и, следовательно, справедливо выражение, записанное на основе принципа возможных перемещений (3.44):

. (3.46)

Если все связи идеальные, то 2-я сумма равна нулю и в проекциях на оси координат равенство (3.46) будет выглядеть следующим образом:

Последнее равенство представляет собой общее вариационное уравнение динамики в проекциях на оси координат, которое позволяет составить дифференциальные уравнения движения механической системы.

Общее вариационное уравнение динамики – это математическое выражение принципа Даламбера-Лагранжа : «При движении системы, подчиненной стационарным, идеальным, удерживающим связям, в каждый данный момент времени сумма элементарных работ всех активных сил, приложенных к системе, и сил инерции на любом возможном перемещении системы равна нулю ».

Пример 2 . Для механической системы (рис. 3.4), состоящей из трех тел определить ускорение груза 1 и натяжение троса 1-2, если: m 1 = 5m ; m 2 = 4m ; m 3 = 8m ; r 2 = 0,5R 2 ; радиус инерции блока 2 i = 1,5r 2 . Каток 3 представляет собой сплошной однородный диск.

Решение

Изобразим силы, которые совершают элементарную работу на возможном перемещении s груза 1:

Запишем возможные перемещения всех тел через возможное перемещение груза 1:

Выразим линейные и угловые ускорения всех тел через искомое ускорение груза 1 (отношения такие же, как и в случае возможных перемещений):

.

Общее вариационное уравнение для данной задачи имеет вид:

Подставляя полученные ранее выражения для активных сил, сил инерции и возможных перемещений, после несложных преобразований получим

Так как s  0, следовательно, равно нулю выражение в скобках, содержащее ускорение а 1 , откуда a 1 = 5g /8,25 = 0,606g .

Для определения натяжения троса, удерживающего груз, освободим груз от троса, заменив действие его искомой реакцией . Под действием заданных сил ,и приложенной к грузу силы инерции
он находится в равновесии. Следовательно, к рассматриваемому грузу (точке) применим принцип Даламбера, т.е. запишем, что
. Отсюда
.

3.8.4. Уравнение Лагранжа 2-го рода

Обобщенные координаты и обобщенные скорости . Любые независимые между собой параметры, однозначно определяющие положение механической системы в пространстве, называют обобщенными координатами . Эти координаты, обозначаемые q 1 ,....q i , могут иметь любую размерность. В частности, обобщенные координаты могут быть перемещениями или углами поворота.

Для рассматриваемых систем число обобщенных координат равно числу степеней свободы. Положение каждой точки системы является однозначной функцией обобщенных координат

Таким образом, движение системы в обобщенных координатах определяется следующими зависимостями:

Первые производные от обобщенных координат называют обобщенными скоростями :
.

Обобщенные силы. Выражение для элементарной работы силы на возможном перемещении
имеет вид:

.

Для элементарной работы системы сил запишем

Используя полученные зависимости, это выражение можно записать в виде:

,

где обобщенная сила, соответствующая i -й обобщенной координате,

. (3.49)

Таким образом, обобщенной силой, соответствующей i -й обобщенной координате, является коэффициент при вариации этой координаты в выражении суммы элементарных работ активных сил на возможном перемещении системы. Для вычисления обобщенной силы необходимо сообщить системе возможное перемещение, при котором изменяется только обобщенная координата q i . Коэффициент при
и будет искомой обобщенной силой.

Уравнения движения системы в обобщенных координатах . Пусть дана механическая система с s степенями свободы. Зная действующие на нее силы, необходимо, составить дифференциальные уравнения движения в обобщенных координатах
. Применим процедуру составления дифференциальных уравнений движения системы – уравнений Лагранжа 2-го рода – по аналогии вывода этих уравнений для свободной материальной точки. Исходя из 2-го закона Ньютона, запишем

Получим аналог этим уравнениям, используя запись для кинетической энергии материальной точки,

Частная производная от кинетической энергии по проекции скорости на ось
равна проекции количества движения на эту ось, т.е.

Чтобы получить необходимые уравнения, вычислим производные по времени:

Полученная система уравнений является уравнениями Лагранжа 2-го рода для материальной точки.

Для механической системы уравнения Лагранжа 2-го рода представим в виде уравнений, в которых вместо проекций активных сил P x , P y , P z используют обобщенные силы Q 1 , Q 2 ,...,Q i и учитывают в общем случае зависимость кинетической энергии от обобщенных координат.

Уравнения Лагранжа 2-го рода для механической системы имеют вид:

. (3.50)

Их можно использовать для изучения движения любой механической системы с геометрическими, идеальными и удерживающими связями.

Пример 3 . Для механической системы (рис. 3.5), данные для которой приведены в предыдущем примере, составить дифференциальное уравнение движения, используя уравнение Лагранжа 2-го рода,

Решение

Механическая система имеет одну степень свободы. За обобщенную координату примем линейное перемещение груза q 1 = s ; обобщенная скорость – . С учетом этого запишем уравнение Лагранжа 2-го рода

.

Составим выражение для кинетической энергии системы

.

Выразим все угловые и линейные скорости через обобщенную скорость:

Теперь получим

Вычислим обобщенную силу, составив выражение элементарной работы на возможном перемещении s всех действующих сил. Без учета сил трения работу в системе производит только сила тяжести груза 1
Запишем обобщенную силу при s , как коэффициент в элементарной работе Q 1 = 5mg . Далее найдем

Окончательно дифференциальное уравнение движения системы будет иметь вид:

Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера.

Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой . Под действием приложенных к ней внешних и внутренних сил и (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение .

Введем в рассмотрение величину

имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции).

Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам и прибавить силу инерции , то полученная система сил будет уравновешенной, т.е. будет

.

Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает . Перенося здесь член в правую часть равенства и придем к последнему соотношению.

Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.

Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики.

Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и , возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.

Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть.