Yhtälö kosini x on yhtä suuri kuin a. Trigonometriset yhtälöt - kaavat, ratkaisut, esimerkit. Faktorisointi

Voit tilata yksityiskohtaisen ratkaisun ongelmaasi!!!

Yhtälöä, joka sisältää tuntemattoman trigonometrisen funktion merkin alla (`sin x, cos x, tan x` tai `ctg x`), kutsutaan trigonometriseksi yhtälöksi, ja niiden kaavoja tarkastellaan edelleen.

Yksinkertaisimmat yhtälöt ovat "sin x=a, cos x=a, tg x=a, ctg x=a", missä "x" on löydettävä kulma, "a" on mikä tahansa luku. Kirjataan ylös kunkin niistä juurikaavat.

1. Yhtälö "sin x=a".

Kohdalle `|a|>1` ei ole ratkaisuja.

Kun `|a| \leq 1`:llä on ääretön määrä ratkaisuja.

Juurikaava: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Yhtälö "cos x=a".

`|a|>1` - kuten sinin tapauksessa, sillä ei ole ratkaisuja reaalilukujen joukossa.

Kun `|a| \leq 1`:llä on ääretön määrä ratkaisuja.

Juurikaava: `x=\pm arccos a + 2\pi n, n \in Z`

Sinin ja kosinin erikoistapaukset kaavioissa.

3. Yhtälö "tg x=a".

Siinä on ääretön määrä ratkaisuja mille tahansa "a":n arvoille.

Juurikaava: `x=arctg a + \pi n, n \in Z`

4. Yhtälö ctg x=a

Siinä on myös ääretön määrä ratkaisuja mille tahansa "a":n arvoille.

Juurikaava: `x=arcctg a + \pi n, n \in Z`

Kaavat trigonometristen yhtälöiden juurille taulukossa

Sinille:
Kosinille:
Tangentille ja kotangentille:
Kaavat käänteisiä trigonometrisiä funktioita sisältävien yhtälöiden ratkaisemiseksi:

Trigonometristen yhtälöiden ratkaisumenetelmät

Minkä tahansa trigonometrisen yhtälön ratkaiseminen koostuu kahdesta vaiheesta:

• muuntamalla se yksinkertaisimmaksi;
• ratkaise yksinkertaisin yhtälö yllä kirjoitetuilla juurikaavoilla ja taulukoilla.

Katsotaanpa tärkeimpiä ratkaisumenetelmiä esimerkkien avulla.

Algebrallinen menetelmä.

Tämä menetelmä sisältää muuttujan korvaamisen ja sen korvaamisen yhtäläisyydellä.

Esimerkki. Ratkaise yhtälö: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0,

tee korvaava: `cos(x+\frac \pi 6)=y, sitten `2y^2-3y+1=0`,

löydämme juuret: `y_1=1, y_2=1/2`, joista seuraa kaksi tapausta:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Vastaus: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Faktorisointi.

Esimerkki. Ratkaise yhtälö: `sin x+cos x=1`.

Ratkaisu. Siirretään kaikki yhtälön ehdot vasemmalle: `sin x+cos x-1=0`. Käyttämällä , muunnamme ja kerroimme vasemman puolen:

"sin x - 2sin^2 x/2=0",

"2sin x/2 cos x/2-2sin^2 x/2=0",

"2sin x/2 (cos x/2-sin x/2) = 0",

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

Vastaus: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Pelkistys homogeeniseksi yhtälöksi

Ensin sinun on vähennettävä tämä trigonometrinen yhtälö johonkin kahdesta muodosta:

"a sin x+b cos x=0" (ensimmäisen asteen homogeeninen yhtälö) tai "a sin^2 x + b sin x cos x +c cos^2 x=0" (toisen asteen homogeeninen yhtälö).

Jaa sitten molemmat osat arvolla "cos x \ne 0" - ensimmäisessä tapauksessa ja "cos^2 x \ne 0" - toisessa tapauksessa. Saamme yhtälöt `tg x`:lle: `a tg x+b=0` ja `a tg^2 x + b tg x +c =0`, jotka on ratkaistava tunnetuilla menetelmillä.

Esimerkki. Ratkaise yhtälö: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Ratkaisu. Kirjoita oikea puoli muotoon `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x',

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

"sin^2 x+sin x cos x — 2 cos^2 x=0".

Tämä on toisen asteen homogeeninen trigonometrinen yhtälö, jaamme sen vasemman ja oikean puolen `cos^2 x \ne 0`, saamme:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2 x+tg x — 2=0'. Otetaan käyttöön korvaava `tg x=t`, jolloin tuloksena on `t^2 + t - 2=0`. Tämän yhtälön juuret ovat `t_1=-2` ja `t_2=1`. Sitten:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z.

Vastaus. `x_1=arctg (-2)+\pi n`, `n \in Z, `x_2=\pi/4+\pi n`, `n \in Z'.

Siirtyminen puolikulmaan

Esimerkki. Ratkaise yhtälö: "11 sin x - 2 cos x = 10".

Ratkaisu. Sovelletaan kaksoiskulmakaavoja, jolloin tuloksena on: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

"4 tg^2 x/2 — 11 tg x/2 +6=0".

Käyttämällä yllä kuvattua algebrallista menetelmää saamme:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z',
2. "tg x/2=3/4", "x_2=arctg 3/4+2\pi n", "n \in Z".

Vastaus. `x_1=2 arctg 2+2\pi n, n \in Z, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Apukulman esittely

Trigonometrisessa yhtälössä "a sin x + b cos x =c", jossa a,b,c ovat kertoimia ja x on muuttuja, jaa molemmat puolet arvolla "sqrt (a^2+b^2)":

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))".

Vasemmalla puolella olevilla kertoimilla on sinin ja kosinin ominaisuudet, eli niiden neliöiden summa on yhtä suuri kuin 1 ja niiden moduulit eivät ole suurempia kuin 1. Merkitään ne seuraavasti: `\frac a(sqrt (a^2) +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, sitten:

`cos \varphi sin x + sin \varphi cos x =C`.

Tarkastellaanpa tarkemmin seuraavaa esimerkkiä:

Esimerkki. Ratkaise yhtälö: `3 sin x+4 cos x=2`.

Ratkaisu. Jaa tasa-arvon molemmat puolet `sqrt:llä (3^2+4^2)`, saamme:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))".

"3/5 sin x+4/5 cos x=2/5".

Merkitään `3/5 = cos \varphi` , `4/5=sin \varphi`. Koska `sin \varphi>0`, `cos \varphi>0`, otamme `\varphi=arcsin 4/5` apukulmaksi. Sitten kirjoitamme yhtäläisyytemme muodossa:

`cos \varphi sin x+sin \varphi cos x=2/5`

Soveltamalla sinin kulmien summan kaavaa kirjoitamme yhtäläisyytemme seuraavassa muodossa:

"sin (x+\varphi)=2/5",

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z'.

Vastaus. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z'.

Murto-rationaaliset trigonometriset yhtälöt

Nämä ovat yhtälöitä murtolukujen kanssa, joiden osoittajat ja nimittäjät sisältävät trigonometrisiä funktioita.

Esimerkki. Ratkaise yhtälö. `\frac (sin x)(1+cos x)=1-cos x.

Ratkaisu. Kerro ja jaa yhtälön oikea puoli `(1+cos x)`:lla. Tuloksena saamme:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

\frac (sin x-sin^2 x)(1+cos x)=0

Ottaen huomioon, että nimittäjä ei voi olla yhtä suuri kuin nolla, saamme `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Yhdistäkäämme murtoluvun osoittaja nollaan: "sin x-sin^2 x=0", "sin x(1-sin x)=0". Sitten "sin x=0" tai "1-sin x=0".

1. "sin x=0", "x=\pi n", "n \in Z".
2. "1-sin x=0", "sin x=-1", "x=\pi /2+2\pi n, n \in Z".

Ottaen huomioon, että ` x \ne \pi+2\pi n, n \in Z`, ratkaisut ovat `x=2\pi n, n \in Z` ja `x=\pi /2+2\pi n` , "n \in Z".

Vastaus. "x=2\pi n", "n \in Z", "x=\pi /2+2\pi n", "n \in Z".

Trigonometriaa ja erityisesti trigonometrisiä yhtälöitä käytetään lähes kaikilla geometrian, fysiikan ja tekniikan aloilla. Opiskelu alkaa 10. luokalla, yhtenäistettyyn valtionkokeeseen on aina tehtäviä, joten yritä muistaa kaikki trigonometristen yhtälöiden kaavat - niistä on varmasti hyötyä sinulle!

Sinun ei kuitenkaan tarvitse edes opetella niitä ulkoa, tärkeintä on ymmärtää ydin ja pystyä johtamaan se. Se ei ole niin vaikeaa kuin miltä näyttää. Katso itse katsomalla video.

Yksinkertaisimmat trigonometriset yhtälöt ratkaistaan ​​yleensä kaavoilla. Haluan muistuttaa, että yksinkertaisimmat trigonometriset yhtälöt ovat:

sinx = a

cosx = a

tgx = a

ctgx = a

x on löydettävä kulma,
a on mikä tahansa luku.

Ja tässä ovat kaavat, joilla voit heti kirjoittaa näiden yksinkertaisimpien yhtälöiden ratkaisut.

Sinille:

Kosinille:

x = ± arccos a + 2π n, n ∈ Z

Tangentille:

x = arctan a + π n, n ∈ Z

Kotangentille:

x = arcctg a + π n, n ∈ Z

Itse asiassa tämä on yksinkertaisimpien trigonometristen yhtälöiden ratkaisemisen teoreettinen osa. Lisäksi kaikki!) Ei mitään. Tämän aiheen virheiden määrä on kuitenkin yksinkertaisesti poissa kaavioista. Varsinkin jos esimerkki poikkeaa hieman mallista. Miksi?

Kyllä, koska monet ihmiset kirjoittavat näitä kirjeitä, ymmärtämättä niiden merkitystä ollenkaan! Hän kirjoittaa muistiin varoen, ettei jotain tapahdu...) Tämä täytyy selvittää. Trigonometria ihmisille tai ihmiset trigonometrialle!?)

Otetaanpa selvää?

Yksi kulma on yhtä suuri kuin arccos a, toinen: -arccos a.

Ja näin tulee aina käymään. Mille tahansa A.

Jos et usko minua, vie hiiri kuvan päälle tai kosketa kuvaa tablet-laitteellasi.) Vaihdoin numeroa A johonkin negatiiviseen. Joka tapauksessa, meillä on yksi kulma arccos a, toinen: -arccos a.

Siksi vastaus voidaan aina kirjoittaa kahdeksi juurisarjaksi:

x 1 = arccos a + 2π n, n ∈ Z

x 2 = - arccos a + 2π n, n ∈ Z

Yhdistetään nämä kaksi sarjaa yhdeksi:

x= ± arccos a + 2π n, n ∈ Z

Ja siinä kaikki. Olemme saaneet yleisen kaavan yksinkertaisimman trigonometrisen yhtälön ratkaisemiseksi kosinilla.

Jos ymmärrät, että tämä ei ole jonkinlaista ylitieteellistä viisautta, vaan vain lyhennetty versio kahdesta vastaussarjasta, Pystyt myös hoitamaan C-tehtäviä. Epäyhtälöillä, juurien valinnalla tietystä intervallista... Siellä vastaus plus/miinus ei toimi. Mutta jos käsittelet vastausta asiallisesti ja jaat sen kahdeksi erilliseksi vastaukseksi, kaikki ratkeaa.) Itse asiassa, siksi tutkimme sitä. Mitä, miten ja missä.

Yksinkertaisimmassa trigonometrisessa yhtälössä

sinx = a

saamme myös kaksi sarjaa juuria. Aina. Ja nämä kaksi sarjaa voidaan myös äänittää yhdellä rivillä. Vain tämä rivi on hankalampi:

x = (-1) n arcsin a + π n, n ∈ Z

Mutta olemus pysyy samana. Matemaatikot yksinkertaisesti suunnittelivat kaavan tehdäkseen yhden syötteen kahden sijasta juurisarjoille. Siinä kaikki!

Tarkastetaanko matemaatikot? Eikä koskaan tiedä...)

Edellisellä oppitunnilla käsiteltiin yksityiskohtaisesti sinin kanssa tehdyn trigonometrisen yhtälön ratkaisua (ilman kaavoja):

Vastaus johti kahteen juurisarjaan:

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Jos ratkaisemme saman yhtälön kaavalla, saamme vastauksen:

x = (-1) n arcsin 0,5 + π n, n ∈ Z

Itse asiassa tämä on keskeneräinen vastaus.) Opiskelijan on tiedettävä se arcsin 0,5 = π /6. Täydellinen vastaus olisi:

x = (-1)n π /6+ π n, n ∈ Z

Tämä herättää mielenkiintoisen kysymyksen. Vastaa kautta x 1; x 2 (tämä on oikea vastaus!) ja yksinäisyyden kautta X (ja tämä on oikea vastaus!) - ovatko ne sama asia vai eivät? Selvitämme nyt.)

Korvaamme vastauksessa x 1 arvot n =0; 1; 2; jne., laskemme, saamme sarjan juuria:

x 1 = π/6; 13π/6; 25π/6 ja niin edelleen.

Samalla korvauksella vastauksena x 2 , saamme:

x2 = 5π/6; 17π/6; 29π/6 ja niin edelleen.

Korvataan nyt arvot n (0; 1; 2; 3; 4...) yksittäisen yleiseen kaavaan X . Eli nostetaan miinus yksi nollatehoon, sitten ensimmäiseen, toiseen jne. Tietysti korvaamme 0:n toiseen termiin; 1; 2 3; 4 jne. Ja laskemme. Saamme sarjan:

x = π/6; 5π/6; 13π/6; 17π/6; 25π/6 ja niin edelleen.

Siinä on kaikki, mitä näet.) Yleinen kaava antaa meille täsmälleen samat tulokset samoin kuin kaksi vastausta erikseen. Kaikki kerralla, järjestyksessä. Matemaatikkoja ei huijattu.)

Kaavat trigonometristen yhtälöiden ratkaisemiseksi tangentin ja kotangentin kanssa voidaan myös tarkistaa. Mutta emme tee.) Ne ovat jo yksinkertaisia.

Kirjoitin kaiken tämän korvaamisen ja tarkistamisen erikseen. Tässä on tärkeää ymmärtää yksi yksinkertainen asia: perustrigonometristen yhtälöiden ratkaisemiseen on kaavoja, vain lyhyt yhteenveto vastauksista. Tämän lyhyyden vuoksi meidän piti lisätä plus/miinus kosiniratkaisuun ja (-1) n siniratkaisuun.

Nämä lisäykset eivät millään tavalla häiritse tehtäviä, joissa sinun tarvitsee vain kirjoittaa vastaus alkeisyhtälöön. Mutta jos sinun on ratkaistava epätasa-arvo tai sitten sinun on tehtävä jotain vastauksella: valitse juuret väliltä, ​​tarkista ODZ jne., nämä lisäykset voivat helposti häiritä henkilöä.

Eli mitä minun pitäisi tehdä? Kyllä, joko kirjoita vastaus kahteen sarjaan tai ratkaise yhtälö/epäyhtälö trigonometrisen ympyrän avulla. Sitten nämä lisäykset katoavat ja elämästä tulee helpompaa.)

Voimme tiivistää.

Yksinkertaisimpien trigonometristen yhtälöiden ratkaisemiseksi on olemassa valmiita vastauskaavoja. Neljä kappaletta. Niillä on hyvä kirjoittaa yhtälön ratkaisu välittömästi muistiin. Esimerkiksi sinun on ratkaistava yhtälöt:

sinx = 0,3

Helposti: x = (-1) n arcsin 0,3 + π n, n ∈ Z

cosx = 0,2

Ei ongelmaa: x = ± kaaret 0,2 + 2π n, n ∈ Z

tgx = 1,2

Helposti: x = arctaani 1,2 + π n, n ∈ Z

ctgx = 3,7

Yksi jäljellä: x= arcctg3,7 + π n, n ∈ Z

cos x = 1,8

Jos sinä loistat tiedosta, kirjoitat vastauksen välittömästi:

x= ± kaaret 1,8 + 2π n, n ∈ Z

silloin sinä loistat jo, tämä... tuo... lätäköstä.) Oikea vastaus: ei ole ratkaisuja. Etkö ymmärrä miksi? Lue mikä on kaarikosini. Lisäksi, jos alkuperäisen yhtälön oikealla puolella on taulukkoarvot sinistä, kosinista, tangentista, kotangentista, - 1; 0; √3; 1/2; √3/2 ja niin edelleen. - vastaus holvien läpi jää kesken. Kaaret on muutettava radiaaneiksi.

Ja jos törmäät eriarvoisuuteen, esim

niin vastaus on:

x πn, n ∈ Z

on harvinaista hölynpölyä, kyllä...) Tässä sinun on ratkaistava trigonometrisen ympyrän avulla. Mitä teemme vastaavassa aiheessa.

Niille, jotka lukevat sankarillisesti näitä rivejä. En voi muuta kuin arvostaa titaanisia ponnistelujasi. Bonus sinulle.)

Bonus:

Kun kirjoitat kaavoja hälyttävässä taistelutilanteessa, kokeneet nörtitkin usein hämmentyvät missä πn, Ja missä 2π n. Tässä on sinulle yksinkertainen temppu. Sisään kaikille arvoiset kaavat πn. Paitsi ainoa kaava, jossa on kaarikosinin. Se seisoo siellä 2πn. Kaksi peen. Avainsana - kaksi. Tässä samassa kaavassa on kaksi merkki alussa. Plussaa ja miinusta. Siellä sun täällä - kaksi.

Jos siis kirjoitit kaksi merkki ennen kaarikosinia, on helpompi muistaa, mitä lopussa tapahtuu kaksi peen. Ja tapahtuu myös toisinpäin. Henkilö kaipaa merkkiä ± , menee loppuun, kirjoittaa oikein kaksi Pien, ja hän tulee järkiinsä. Jotain on edessä kaksi merkki! Henkilö palaa alkuun ja korjaa virheen! Kuten tämä.)

Jos pidät tästä sivustosta...

Muuten, minulla on sinulle pari muuta mielenkiintoista sivustoa.)

Voit harjoitella esimerkkien ratkaisemista ja selvittää tasosi. Testaus välittömällä vahvistuksella. Opitaan - mielenkiinnolla!)

Voit tutustua funktioihin ja johdannaisiin.

Zakharova Ljudmila Vladimirovna
MBOU "Secondary school No. 59" Barnaulista
matematiikan opettaja [sähköposti suojattu]

№1 Yksinkertaisimmat trigonometriset yhtälöt

Kohde: 1. Johda kaavat muodon yksinkertaisimpien trigonometristen yhtälöiden ratkaisuille sinx =a, cosx=a, tgx=a, ctgx=a;

2. Opi ratkaisemaan yksinkertaisia ​​trigonometrisiä yhtälöitä kaavojen avulla.

Laitteet: 1) Taulukot trigonometristen funktioiden y= kaavioilla sinx, y=cosx, y=tgx, y=ctgx; 2) Käänteisten trigonometristen funktioiden arvojen taulukko; 3) Yhteenvetotaulukko kaavoista yksinkertaisten trigonometristen yhtälöiden ratkaisemiseksi.

Luentotuntisuunnitelma:

1 .Yhtälön juurien kaavojen johtaminen

a) sinx =a,

b) cosx= a,

c) tgx= a,

d) ctgx= A.

2 . Suullinen frontaalityö saatujen kaavojen vahvistamiseksi.

3 . Kirjallinen työ opiskelun aineiston vahvistamiseksi

Algebrassa, geometriassa, fysiikassa ja muissa oppiaineissa kohtaamme erilaisia ​​ongelmia, joiden ratkaisemiseen liittyy yhtälöiden ratkaiseminen. Olemme tutkineet trigonometristen funktioiden ominaisuuksia, joten on luonnollista kääntyä yhtälöiden puoleen, joissa tuntematon on funktiomerkin alla

Määritelmä: Muodon yhtälöt sinx = a , cosx= a , tgx= a , ctgx= A kutsutaan yksinkertaisimmiksi trigonometrisiksi yhtälöiksi.

On erittäin tärkeää oppia ratkaisemaan yksinkertaisimmat trigonometriset yhtälöt, koska kaikki menetelmät ja tekniikat trigonometristen yhtälöiden ratkaisemiseksi koostuvat niiden pelkistämisestä yksinkertaisimpiin.

Aloitetaan johtamalla kaavoja, jotka "aktiivisesti" toimivat trigonometristen yhtälöiden ratkaisemisessa.

1. Yhtälöt muotoa sinx = a.

Ratkaistaan ​​yhtälö sinx = a graafisesti. Tätä varten rakennamme yhteen koordinaattijärjestelmään funktioiden y=sinx ja y= kuvaajat A.

1) Jos A> 1 ja A synti x= A ei ole ratkaisuja, koska suoralla ja siniaallolla ei ole yhteisiä pisteitä.

2) Jos -1a a ylittää siniaallon äärettömän monta kertaa. Tämä tarkoittaa, että yhtälö sinx= a on äärettömän monta ratkaisua.

Koska sinijakso on 2 , sitten yhtälön ratkaisemiseksi sinx= a riittää löytää kaikki ratkaisut mille tahansa segmentille, jonka pituus on 2.

Yhtälön ratkaiseminen [-/2; /2] arcsinin x= määritelmän mukaan arcsin a, ja kohdassa x=-arcsin a. Kun otetaan huomioon funktion у=sinx jaksollisuus, saadaan seuraavat lausekkeet

x = -arcsin a+2n, n Z.

Molemmat ratkaisusarjat voidaan yhdistää

X = (-1) n arcsin a+n, nZ.

Seuraavissa kolmessa tapauksessa he käyttävät mieluummin yksinkertaisempia suhteita yleisen kaavan sijaan:

Jos A=-1, sitten sin x =-1, x=-/2+2n

Jos A=1, sitten sin x =1, x =/2+2n

Jos a= 0, sitten sin x =0. x = n,

Esimerkki: Ratkaise yhtälö sinx = 1/2.

Luodaan kaavoja ratkaisuille x = kaari 1/2+ 2n

X= - arcsin a+2n

Lasketaan arvo arcsin1/2. Korvataan löydetty arvo ratkaisukaavoihin

x=5/6+2n

tai yleisen kaavan mukaan

X = (-1) n arcsin 1/2+n,

X = (-1) n /6 + n,

2. Muodon yhtälöt cosx= a.

Ratkaistaan ​​yhtälö cosx= a myös graafisesti piirtämällä funktiot y= cosx ja y= A.

1) Jos 1, niin yhtälö cosx= a ei ole ratkaisuja, koska kaavioilla ei ole yhteisiä pisteitä.

2) Jos -1 a cosx= a on ääretön määrä ratkaisuja.

Löydämme kaikki ratkaisut cosx= a pituudella 2, koska kosinin jakso on 2.

Kaarikosinin määritelmän mukaan yhtälön ratkaisu on x= arcos a. Kun otetaan huomioon kosinifunktion pariteetti, yhtälön [-;0] ratkaisu on x=-arcos a.

Siten yhtälön ratkaiseminen cosx= a x= + arcos a+ 2 n,

Kolmessa tapauksessa emme käytä yleistä kaavaa, vaan yksinkertaisempia suhteita:

Jos A=-1, sitten cosx =-1, x =-/2+2n

Jos A=1, sitten cosx =1, x = 2n,

Jos a=0, niin cosx=0. x =/2+n

Esimerkki: Ratkaise yhtälö cos x = 1/2,

Luodaan kaavoja ratkaisuille x=arccos 1/2+ 2n

Lasketaan arvo arccos1/2.

Korvataan löydetty arvo ratkaisukaavoihin

X= + /3+ 2n, nZ.

Muodon yhtälöt tgx= a.

Koska tangentin jakso on yhtä suuri, niin yhtälön kaikkien ratkaisujen löytämiseksi tgx= a, riittää löytää kaikki ratkaisut millä tahansa pituudella. Arktangentin määritelmän mukaan yhtälön (-/2; /2) ratkaisu on arktaani a. Kun otetaan huomioon funktion jakso, kaikki yhtälön ratkaisut voidaan kirjoittaa muotoon

x = arctaani a+ n, nZ.

Esimerkki: Ratkaise yhtälö rusketus x = 3/3

Luodaan kaava x=:n ratkaisemiseksi arctan 3/3 +n, nZ.

Lasketaan arktangentin arvo arctan 3/3= /6 siis

X=/6+ n, nZ.

Yhtälön ratkaisukaavan johtaminen Kanssa tgx= a voidaan tarjota opiskelijoille.

Esimerkki.

Ratkaise yhtälö ctg x = 1.

x = arcсtg 1 + n, nZ,

X = /4 + n, nZ.

Tutkitun materiaalin tuloksena opiskelijat voivat täyttää taulukon:

"Trigonometristen yhtälöiden ratkaiseminen."

yhtälö

Harjoituksia opitun materiaalin lujittamiseksi.

(Suullinen) Mikä kirjoitetuista yhtälöistä voidaan ratkaista kaavoilla:

a) x= (-1) n arcsin a+n, nZ;

b) x= + arcos a+ 2n?

cos x = 2/2, tan x = 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 .

Millä seuraavista yhtälöistä ei ole ratkaisuja?

Ratkaise yhtälöt:

a) sin x = 0; e) sin x = 2/2; h) sin x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

d) tan x = 3; g) pinnasänky x = -1; j) rusketus x = 1/3.

3. Ratkaise yhtälöt:

a) sin 3x = 0; e) 2cos x = 1;

b) cos x/2 = 1/2; e) 3 tg 3x = 1;

d) sin x/4 = 1; g) 2cos(2x+ /5) = 3.

Näitä yhtälöitä ratkaistaessa on hyödyllistä kirjoittaa muistiin muodon yhtälöiden ratkaisemisen säännöt synti V x = a, Ja Kanssa synti V x = a, | a|1.

Synti V x = a, |a|1.

V x = (-1) n arcsin a+n, nZ,

x= (-1) n 1/ V arcsin a+n/ V, nZ.

Yhteenveto oppitunnista:

Tänään luokassa johdimme kaavoja yksinkertaisten trigonometristen yhtälöiden ratkaisemiseen.

Tarkastelimme esimerkkejä yksinkertaisten trigonometristen yhtälöiden ratkaisemisesta.

Täytimme taulukon, jota käytämme yhtälöiden ratkaisemiseen.

Kotitehtävät.

№2 Trigonometristen yhtälöiden ratkaiseminen

Kohde: Tutkimusmenetelmiä trigonometristen yhtälöiden ratkaisemiseksi: 1) pelkistävissä neliöllisiksi 2) pelkistävissä homogeenisiksi trigonometrisiksi yhtälöiksi.

Kehittää opiskelijoiden havainnointikykyä erilaisten trigonometristen yhtälöiden ratkaisumenetelmien käytössä.

Etutyötä opiskelijoiden kanssa.

Mitkä ovat trigonometristen yhtälöiden juurien kaavat? cos x= a, sin x= a, tgx = a, ctg x = a.

Ratkaise yhtälöt (suullisesti):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1,5, sin x=0.

Etsi virheet ja mieti virheiden syitä.

cos x=1/2, x= + /6+2k,k Z.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x = 1+ k, kZ.

2. Uuden materiaalin opiskelu.

Tämä oppitunti kattaa joitain yleisimmistä menetelmistä trigonometristen yhtälöiden ratkaisemiseksi.

Trigonometriset yhtälöt pelkistetty neliöllisiksi.

Tämä luokka voi sisältää yhtälöitä, jotka sisältävät yhden funktion (sini tai kosini) tai kaksi saman argumentin funktiota, mutta yksi niistä pelkistetään toiseen käyttämällä trigonometrisiä perusidentiteettejä.

Esimerkiksi, jos cosх tulee yhtälöön parillisilla potenssilla, korvaamme sen 1-sin 2 x, jos sin 2 x, niin korvaamme sen 1-cos 2 x.

Esimerkki.

Ratkaise yhtälö: 8 sin 2 x - 6sin x -5 =0.

Ratkaisu: Merkitään sin x=t, sitten 8t 2 - 6t - 5=0,

D = 196,

T1 = -1/2, t2 = -5/4.

Suoritetaan käänteinen substituutio ja ratkaistaan ​​seuraavat yhtälöt.

X = (-1) k+1 /6+ k, kZ.

Koska -5/4>1, yhtälöllä ei ole juuria.

Vastaus: x=(-1) k+1 /6+ k, kZ.

Konsolidaatioharjoitusten ratkaiseminen.

Ratkaise yhtälö:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1 = 0.

Homogeeniset trigonometriset yhtälöt.

Määritelmä: 1) Muodon yhtälöa sinx + b cosx=0, (a=0, b=0) kutsutaan ensimmäisen asteen homogeeniseksi yhtälöksi sin x:n ja cos x:n suhteen.

Tämä yhtälö ratkaistaan ​​jakamalla molemmat puolet cosx 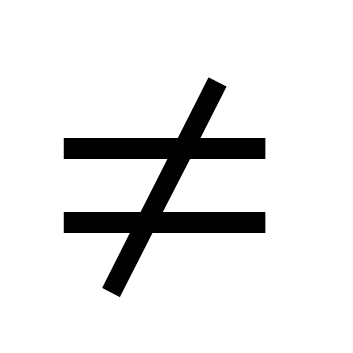0. Tulos on yhtälö atgx+ b=0.

2) Muodon yhtälöa synti 2 x + b sinx cosx + c cos 2 x =0 kutsutaan toisen asteen homogeeniseksi yhtälöksi, jossa a, b, c ovat mitä tahansa lukuja.

Jos a = 0, niin ratkaisemme yhtälön jakamalla molemmat puolet cos 2 x 0. Tuloksena saadaan yhtälö atg 2 x+ btgx+с =0.

Kommentti: Muodon yhtälöa synti mx + b cos mx=0 tai

a synti 2 mx + b synti mx cos mx + c cos 2 mx =0 ovat myös homogeenisia. Niiden ratkaisemiseksi yhtälön molemmat puolet jaetaan cos:lla mx=0 tai cos 2 mx=0

3) Erilaiset yhtälöt, jotka eivät ole alun perin homogeenisia yhtälöitä, voidaan pelkistää homogeenisiksi yhtälöiksi. Esimerkiksi,synti 2 mx + b synti mx cos mx + c cos 2 mx = d, Ja a sinx + b cosx= d. Näiden yhtälöiden ratkaisemiseksi sinun on kerrottava oikea puoli "trigonometrinen yksikkö" nuo. päällä synti 2 x + cos 2 x ja suorittaa matemaattisia muunnoksia.

Harjoituksia opitun materiaalin vahvistamiseksi:

1) 2sin x-3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx = 2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx = 2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. Oppitunnin yhteenveto. Kotitehtävät.

Tällä oppitunnilla voit ryhmän valmiudesta riippuen harkita muodon yhtälöiden ratkaisemista a sin mx +b cos mx=c, missä a, b, c eivät ole yhtä aikaa nolla.

Vahvistavat harjoitukset:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x = 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 Trigonometristen yhtälöiden ratkaiseminen

Kohde: 1) Tutkia menetelmää trigonometristen yhtälöiden ratkaisemiseksi tekijöiden avulla; oppia ratkaisemaan trigonometrisiä yhtälöitä käyttämällä erilaisia ​​trigonometrisiä kaavoja;

2) Tarkista: opiskelijoiden tieto kaavoista yksinkertaisten trigonometristen yhtälöiden ratkaisemiseksi; kyky ratkaista yksinkertaisia ​​trigonometrisiä yhtälöitä.

Tuntisuunnitelma:

Kotitehtävien tarkistaminen.

Matemaattinen sanelu.

Uuden materiaalin oppiminen.

Itsenäinen työ.

Yhteenveto oppitunnista. Kotitehtävät.

Oppitunnin edistyminen:

Kotitehtävien tarkistaminen (trigonometristen yhtälöiden ratkaisut kirjoitetaan lyhyesti taululle).

Matemaattinen sanelu.

KOHDASSA 1

1. Mitä yhtälöitä kutsutaan yksinkertaisimmiksi trigonometrisiksi yhtälöiksi?

2. Mikä on muodon yhtälön nimia sinx + b cosx=0? Ilmoita tapa ratkaista se.

3. Kirjoita muistiin yhtälön juurten kaava tgx = a(ctg x= a).

4. Kirjoita muistiin muodon yhtälöiden juurten kaavat cosx= a, Missä A=1, A=0, A=-1.

5. Kirjoita muistiin yhtälön juurien yleinen kaava synti x= a, | a|

6. Miten muodon yhtälöt ratkaistaana cosx= b, | b|

KLO 2

1. Kirjoita muistiin yhtälöiden juurten kaavat cosx= a,| a|

2. Kirjoita muistiin yhtälön juurten yleinen kaava

= a, | a|

3. Mitä muodon yhtälöitä kutsutaan? synti x= a, tgx = a, synti x= a?

4. Kirjoita muistiin yhtälön juurten kaavat synti x= a, Jos A=1, A=0, A=-1.

5. Miten muodon yhtälöt ratkaistaan synti a x= b, | b|

6. Mitä yhtälöitä kutsutaan toisen asteen homogeenisiksi yhtälöiksi? Miten ne ratkaistaan?

Uuden materiaalin oppiminen.

Faktorisointimenetelmä.

Yksi yleisimmin käytetyistä menetelmistä trigonometristen yhtälöiden ratkaisemiseksi on faktorointimenetelmä.

Jos yhtälö f(x) =0 voidaan esittää muodossa f 1 (x) f 2 (x) =0, niin ongelma pelkistetään ratkaisemaan kaksi yhtälöä f 1 (x) = 0, f 2 (x) = 0 .

(Oppilaiden kanssa on hyödyllistä muistaa sääntö Tekijöiden tulo on nolla, jos ainakin yksi tekijöistä on yhtä suuri kuin nolla ja muilla on järkeä»)

Tutkitun aineiston konsolidointi ratkaisemalla monimutkaisia ​​yhtälöitä.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0; (itse)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x = 0;

5) sin 2x – cosx=0; 6) 4 cos 2 x -1 = 0; (2 tapaa)

7) cosx+ cos3x=0; 8) sin 3x = sin 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0 (itse)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

Itsenäinen työ.

Vaihtoehto-1 Vaihtoehto-2

1) 6 sin 2 x+ 5sin x -1 = 0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. Oppitunnin yhteenveto. Kotitehtävät.