Koosinus x võrrand on võrdne a. Trigonomeetrilised võrrandid - valemid, lahendid, näited. Faktoriseerimine
Saate tellida oma probleemile üksikasjaliku lahenduse !!!
Võrdsust, mis sisaldab tundmatut trigonomeetrilise funktsiooni märgi all (`sin x, cos x, tan x` või` ctg x`), nimetatakse trigonomeetriliseks võrrandiks ja me käsitleme nende valemeid edasi.
Lihtsamaid võrrandeid nimetatakse "sin x = a, cos x = a, tg x = a, ctg x = a", kus" x" on leitav nurk, "a" on suvaline arv. Kirjutame üles igaühe juurvalemid.
1. Võrrand "sin x = a".
Lahendusel „| a |> 1” pole lahendusi.
`| a | jaoks \ leq 1`-l on lõpmatu arv lahendeid.
Juurvalem: `x = (- 1) ^ n arcsin a + \ pi n, n \ in Z'
2. Võrrand "cos x = a".
`| a |> 1` puhul - nagu siinuse puhul, pole sellel reaalarvude hulgas lahendeid.
`| a | jaoks \ leq 1`-l on lõpmatu arv lahendeid.
Juurvalem: `x = \ pm arccos a + 2 \ pi n, n \ in Z'
Siinuse ja koosinuse erijuhud graafikutes. 
3. Võrrand "tg x = a".
Sellel on lõpmatu arv lahendusi mis tahes "a" väärtuste jaoks.
Juurvalem: `x = arctan a + \ pi n, n \ in Z`
4. Võrrand „ctg x = a”.
Sellel on ka lõpmatu arv lahendusi mis tahes "a" väärtuste jaoks.
Juurvalem: `x = arcctg a + \ pi n, n \ in Z`
Tabeli trigonomeetriliste võrrandite juurte valemid
Siinuse jaoks: 
Koosinuse jaoks: 
Tangensi ja kotangensi jaoks: 
Valemid pöördtrigonomeetrilisi funktsioone sisaldavate võrrandite lahendamiseks:
Trigonomeetriliste võrrandite lahendamise meetodid
Mis tahes trigonomeetrilise võrrandi lahendus koosneb kahest etapist:
- kasutades teisendage see lihtsaimaks;
- lahendage saadud lihtsaim võrrand, kasutades ülaltoodud juurvalemeid ja tabeleid.
Vaatame peamiste lahendusmeetodite näiteid.
Algebraline meetod.
Selle meetodi puhul tehakse muutuja asendamine ja asendamine võrdsusega.
Näide. Lahendage võrrand: "2cos ^ 2 (x + \ frac \ pi 6) -3sin (\ frac \ pi 3 - x) + 1 = 0"
"2cos ^ 2 (x + \ frac \ pi 6) -3cos (x + \ frac \ pi 6) + 1 = 0",
teeme muudatuse: "cos (x + \ frac \ pi 6) = y", siis" 2y ^ 2-3y + 1 = 0",
leiame juured: `y_1 = 1, y_2 = 1/2`, millest järgneb kaks juhtumit:
1.` cos (x + \ frac \ pi 6) = 1`, `x + \ frac \ pi 6 = 2 \ pi n`,` x_1 = - \ frac \ pi 6 + 2 \ pi n`.
2.` cos (x + \ frac \ pi 6) = 1/2`, `x + \ frac \ pi 6 = \ pm arccos 1/2 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`.
Vastus: `x_1 = - \ frac \ pi 6 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`.
Faktoriseerimine.
Näide. Lahendage võrrand: `sin x + cos x = 1`.
Lahendus. Liigutage kõik võrdsuse liikmed vasakule: "sin x + cos x-1 = 0". Vasaku külje kasutamine, teisendamine ja faktoristamine:
"sin x - 2sin ^ 2 x / 2 = 0",
"2sin x / 2 cos x / 2-2sin ^ 2 x / 2 = 0",
"2sin x / 2 (cos x / 2-sin x / 2) = 0",
- "sin x / 2 = 0", "x / 2 = \ pi n", "x_1 = 2 \ pi n".
- "cos x / 2-sin x / 2 = 0", "tg x / 2 = 1", "x / 2 = arctan 1+ \ pi n", "x / 2 = \ pi / 4 + \ pi n" , `x_2 = \ pi / 2 + 2 \ pi n`.
Vastus: `x_1 = 2 \ pi n`, ` x_2 = \ pi / 2 + 2 \ pi n`.
Taandamine homogeenseks võrrandiks
Esiteks peate selle trigonomeetrilise võrrandi viima ühte kahest tüübist:
`a sin x + b cos x = 0` (esimese astme homogeenne võrrand) või` a sin ^ 2 x + b sin x cos x + c cos ^ 2 x = 0` (teise astme homogeenne võrrand).
Seejärel jagage mõlemad osad arvuga "cos x \ ne 0" - esimesel juhul ja "cos ^ 2 x \ ne 0" - teisel juhul. Saame võrrandid tg x: a tg x + b = 0 ja a tg ^ 2 x + b tg x + c = 0 jaoks, mis tuleb teadaolevate meetoditega lahendada.
Näide. Lahendage võrrand: `2 sin ^ 2 x + sin x cos x - cos ^ 2 x = 1`.
Lahendus. Kirjutage parem pool ümber järgmiselt: "1 = sin ^ 2 x + cos ^ 2 x":
`2 sin ^ 2 x + sin x cos x - cos ^ 2 x =` `sin ^ 2 x + cos ^ 2 x`,
`2 sin ^ 2 x + sin x cos x - cos ^ 2 x -` `sin ^ 2 x - cos ^ 2 x = 0`
"sin ^ 2 x + sin x cos x - 2 cos ^ 2 x = 0".
See on teise astme homogeenne trigonomeetriline võrrand, jagame selle vasaku ja parema külje `cos ^ 2 x \ ne 0`ga, saame:
`\ frac (sin ^ 2 x) (cos ^ 2 x) + \ frac (sin x cos x) (cos ^ 2 x) - \ frac (2 cos ^ 2 x) (cos ^ 2 x) = 0
"tg ^ 2 x + tg x - 2 = 0". Sisestame asenduslause "tg x = t", mille tulemusena on "t ^ 2 + t - 2 = 0". Selle võrrandi juured on "t_1 = -2" ja "t_2 = 1". Seejärel:
- "tg x = -2", "x_1 = arctg (-2) + \ pi n", "n \ in Z"
- "tg x = 1", "x = arctan 1+ \ pi n", "x_2 = \ pi / 4 + \ pi n", " n \ in Z".
Vastus. `x_1 = arctg (-2) + \ pi n`,` n \ in Z, `x_2 = \ pi / 4 + \ pi n`, ` n \ in Z.
Mine poolnurka
Näide. Lahendage võrrand: `11 sin x - 2 cos x = 10`.
Lahendus. Rakendage topeltnurga valemeid, mille tulemuseks on `22 sin (x / 2) cos (x / 2) -`` 2 cos ^ 2 x / 2 + 2 sin ^ 2 x / 2 =` `10 sin ^ 2 x / 2 +10 cos ^ 2 x / 2`
"4 tg ^ 2 x / 2 - 11 tg x / 2 + 6 = 0"
Kasutades ülaltoodud algebralist meetodit, saame:
- "tg x / 2 = 2", "x_1 = 2 arctan 2 + 2 \ pi n", "n \ in Z",
- "tg x / 2 = 3 / 4", x_2 = arctan 3/4 + 2 \ pi n", "n \ in Z".
Vastus. `x_1 = 2 arctan 2 + 2 \ pi n, n \ in Z`,` x_2 = arctan 3/4 + 2 \ pi n`, `n \ in Z.
Sisestage abinurk
Trigonomeetrilises võrrandis `a sin x + b cos x = c`, kus a, b, c on koefitsiendid ja x on muutuja, jagame mõlemad pooled väärtusega` sqrt (a ^ 2 + b ^ 2) `:
`\ frac a (sqrt (a ^ 2 + b ^ 2)) sin x +` `\ frac b (sqrt (a ^ 2 + b ^ 2)) cos x = '' \ frac c (sqrt (a ^ 2) + b ^ 2)) `.
Vasakpoolsetel koefitsientidel on siinuse ja koosinuse omadused, nimelt on nende ruutude summa võrdne 1-ga ja absoluutväärtused ei ole suuremad kui 1. Tähistame neid järgmiselt: `\ frac a (sqrt ( a ^ 2 + b ^ 2)) = cos \ varphi` , `\ frac b (sqrt (a ^ 2 + b ^ 2)) = sin \ varphi`,` \ frac c (sqrt (a ^ 2 + b ^ 2)) = C`, siis:
`cos \ varphi sin x + sin \ varphi cos x = C`.
Vaatame lähemalt järgmist näidet:
Näide. Lahendage võrrand: `3 sin x + 4 cos x = 2`.
Lahendus. Jagage võrdsuse mõlemad pooled `sqrt (3 ^ 2 + 4 ^ 2)`ga, saame:
`\ frac (3 sin x) (sqrt (3 ^ 2 + 4 ^ 2)) +` `\ frac (4 cos x) (sqrt (3 ^ 2 + 4 ^ 2)) = '' \ frac 2 (sqrt (3 ^ 2 + 4 ^ 2)) `
"3/5 sin x + 4/5 cos x = 2/5".
Tähistame `3/5 = cos \ varphi`, ` 4/5 = sin \ varphi`. Kuna `sin \ varphi> 0`,` cos \ varphi> 0`, siis võtame abinurgaks `\ varphi = arcsin 4 / 5`. Seejärel kirjutame oma võrdsuse kujul:
`cos \ varphi sin x + sin \ varphi cos x = 2 / 5`
Rakendades siinuse nurkade summa valemit, kirjutame oma võrdsuse järgmisel kujul:
"sin (x + \ varphi) = 2/5",
`x + \ varphi = (- 1) ^ n arcsin 2/5 + \ pi n`,` n \ in Z,
`x = (- 1) ^ n arcsin 2/5-` `artsin 4/5 + \ pi n`, n \ in Z.
Vastus. `x = (- 1) ^ n arcsin 2/5-` `artsin 4/5 + \ pi n`, n \ in Z.
Murdratsionaaltrigonomeetrilised võrrandid
Need on võrdsused murdudega, mille lugejates ja nimetajates on trigonomeetrilised funktsioonid.
Näide. Lahenda võrrand. `\ frac (sin x) (1 + cos x) = 1-cos x.
Lahendus. Korrutage ja jagage võrdsuse parem külg arvuga „(1 + cos x)”. Selle tulemusena saame:
`\ frac (sin x) (1 + cos x) = '' \ frac ((1-cos x) (1 + cos x)) (1 + cos x)"
`\ frac (sin x) (1 + cos x) =` `\ frac (1-cos ^ 2 x) (1 + cos x)
`\ frac (sin x) (1 + cos x) =` `\ frac (sin ^ 2 x) (1 + cos x)
`\ frac (sin x) (1 + cos x) -`` \ frac (sin ^ 2 x) (1 + cos x) = 0
`\ frac (sin x-sin ^ 2 x) (1 + cos x) = 0
Arvestades, et nimetaja ei saa olla võrdne nulliga, saame `1 + cos x \ ne 0`,` cos x \ ne -1`, `x \ ne \ pi + 2 \ pi n, n \ in Z`.
Võrdsusta murru lugeja nulliga: "sin x-sin ^ 2 x = 0", sin x (1-sin x) = 0". Siis "sin x = 0" või "1-sin x = 0".
- "sin x = 0", "x = \ pi n", "n \ in Z".
- "1-sin x = 0", "sin x = -1", "x = \ pi / 2 + 2 \ pi n, n \ in Z".
Arvestades, et `x \ ne \ pi + 2 \ pi n, n \ in Z, on lahendused: x = 2 \ pi n, n \ in Z ja `x = \ pi / 2 + 2 \ pi n` , "n \ in Z".
Vastus. "x = 2 \ pi n", " n \ in Z", "x = \ pi / 2 + 2 \ pi n", " n \ in Z".
Trigonomeetriat ja eriti trigonomeetrilisi võrrandeid kasutatakse peaaegu kõigis geomeetria, füüsika ja inseneri valdkondades. Õppetöö algab 10. klassist, eksamil on kindlasti ülesanded, nii et proovige meeles pidada kõiki trigonomeetriliste võrrandite valemeid - need tulevad kindlasti kasuks!
Siiski pole vaja neid isegi pähe õppida, peaasi, et mõistaksite olemust ja suudaksite neid järeldada. See pole nii raske, kui see kõlab. Vaadake videot vaadates ise.
Lihtsamaid trigonomeetrilisi võrrandeid lahendatakse tavaliselt valemitega. Lubage mul teile meelde tuletada, et järgmisi trigonomeetrilisi võrrandeid nimetatakse kõige lihtsamateks:
sinx = a
cosx = a
tgx = a
ctgx = a
x on leitav nurk,
a - mis tahes arv.
Ja siin on valemid, millega saab nende lihtsamate võrrandite lahendid kohe kirja panna.
Siinuse jaoks:
Koosinuse jaoks:
х = ± arccos a + 2π n, n ∈ Z
Tangensi jaoks:
x = arctan a + π n, n ∈ Z
Kotangensi jaoks:
x = arcctg a + π n, n ∈ Z
Tegelikult on see kõige lihtsamate trigonomeetriliste võrrandite lahendamise teoreetiline osa. Pealegi kõike!) Üldse mitte midagi. Selle teema vigade arv on aga lihtsalt mastaapne. Eriti kui näide mallist veidi kõrvale kaldub. Miks?
Jah, kuna paljud inimesed kirjutavad need kirjad üles, ei saa üldse aru nende tähendusest! Ettevaatlikult kirjutab ta üles, ükskõik kuidas miski ka ei juhtuks...) Sellega tuleb tegeleda. Inimeste jaoks trigonomeetria või ikkagi inimesed trigonomeetria jaoks!?)
Kas mõtleme selle välja?
Üks nurk on võrdne arccos a, teine: -arccos a.
Ja see töötab alati nii. Iga a.
Kui te mind ei usu, hõljutage kursorit pildi kohal või puudutage tahvelarvutis pilti.) Muutsin numbrit a mõnele negatiivsele. Igatahes saime ühe nurga arccos a, teine: -arccos a.
Seetõttu saab vastuse alati kirjutada kahe juurte seeria kujul:
x 1 = arccos a + 2π n, n ∈ Z
x 2 = - arccos a + 2π n, n ∈ Z
Ühendame need kaks seeriat üheks:
x = ± arccos a + 2π n, n ∈ Z
Ja ongi kõik. Sai üldise valemi lihtsaima trigonomeetrilise võrrandi koosinusega lahendamiseks.
Kui mõistad, et see pole mingi üliteaduslik tarkus, vaid lihtsalt kahe vastuse seeria lühendatud märge, teie ja ülesanne "C" on õlal. Ebavõrdsustega, antud intervalli juurte valikuga ... Seal pluss/miinus vastus ei veere. Ja kui käsitlete vastust asjalikult ja jagate selle kaheks eraldi vastuseks, on kõik otsustatud.) Tegelikult saame sellest aru. Mida, kuidas ja kus.
Kõige lihtsamas trigonomeetrilises võrrandis
sinx = a
samuti saadakse kaks seeriat juuri. On alati. Ja neid kahte sarja saab ka salvestada üks rida. Ainult see rida on kavalam:
х = (-1) n arcsin a + π n, n ∈ Z
Kuid olemus jääb samaks. Matemaatikud koostasid lihtsalt valemi, et teha kahe juurte seeria kirje asemel üks. Ja see ongi kõik!
Kontrollime matemaatikuid? Ja siis ei tea kunagi...)
Eelmises tunnis analüüsiti üksikasjalikult siinuse trigonomeetrilise võrrandi lahendust (ilma valemiteta):
Vastus andis kaks juurte seeriat:
x 1 = π / 6 + 2π n, n ∈ Z
x 2 = 5π / 6 + 2π n, n ∈ Z
Kui lahendame sama võrrandi valemiga, saame vastuse:
x = (-1) n arcsin 0,5 + π n, n ∈ Z
Tegelikult on see lõpetamata vastus.) Õpilane peab seda teadma arcsin 0,5 = π / 6. Täielik vastus oleks järgmine:
x = (-1) n π / 6+ π n, n ∈ Z
See tõstatab huvitava küsimuse. Vasta kaudu x 1; x 2 (see on õige vastus!) ja läbi üksildaste X (ja see on õige vastus!) - sama asi või mitte? Saame nüüd teada.)
Asenda vastuseks sõnaga x 1 tähenduses n = 0; üks; 2; ja nii edasi, me loendame, saame rea juuri:
x 1 = π/6; 13π / 6; 25π / 6 jne.
Sama asendusega vastuses -ga x 2 , saame:
x 2 = 5π / 6; 17π / 6; 29π / 6 jne.
Nüüd asendame väärtused n (0; 1; 2; 3; 4 ...) üksildase üldvalemisse X ... See tähendab, et tõstame miinus ühe nulli, seejärel esimesse, teise jne. Ja loomulikult asendame teises liikmes 0; üks; 2 3; 4 jne. Ja me loeme. Saame sarja:
x = π / 6; 5π / 6; 13π / 6; 17π / 6; 25π / 6 jne.
See on kõik, mida näete.) Üldvalem annab meile täpselt samad tulemused, kui kaks vastust eraldi. Ainult korraga, järjekorras. Ärge laske matemaatikutel end petta.)
Samuti saab kontrollida tangensi ja kotangensiga trigonomeetriliste võrrandite lahendamise valemeid. Aga me ei tee seda.) Need on nii lihtsad.
Olen kõike seda asendamist ja kontrollimist meelega kirjeldanud. Siin on oluline mõista üht lihtsat asja: elementaarsete trigonomeetriliste võrrandite lahendamiseks on valemid, vaid lühike ülevaade vastustest. Selle lühiduse huvides pidin koosinuslahusesse sisestama pluss/miinus ja siinuslahusesse (-1) n.
Need lisad ei sega kuidagi ülesannetesse, kus tuleb lihtsalt elementaarvõrrandi vastus kirja panna. Kuid kui teil on vaja ebavõrdsust lahendada või siis vastusega midagi ette võtta: valida intervalli juured, kontrollida ODZ-d jne, võivad need lisad inimese kergesti häirida.
Ja mida teha? Jah, kirjutage vastus kahes seerias üles või lahendage võrrand / ebavõrdsus piki trigonomeetrilist ringi. Siis need lisad kaovad ja elu muutub lihtsamaks.)
Võime kokkuvõtte teha.
Lihtsamate trigonomeetriliste võrrandite lahendamiseks on valmis vastusevalemid. Neli tükki. Need sobivad võrrandi lahendi koheseks salvestamiseks. Näiteks peate lahendama võrrandid:
sinx = 0,3
Lihtne: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Pole probleemi: х = ± kaared 0,2 + 2π n, n ∈ Z
tgx = 1,2
Lihtsalt: x = arctan 1,2 + π n, n ∈ Z
ctgx = 3,7
Üks jäänud: x = arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Kui teadmistest särades kirjutad kohe vastuse:
x = ± kaared 1,8 + 2π n, n ∈ Z
siis juba särad, see ... see ... lombist.) Õige vastus: lahendusi pole. Kas saate aru, miks? Lugege, mis on arkosiin. Lisaks, kui siinuse, koosinuse, puutuja, kotangensi tabeliväärtused on algse võrrandi paremal küljel, - 1; 0; √3; 1/2; √3/2 jne. - vastus läbi kaare jääb lõpetamata. Kaared tuleb tõlkida radiaanidesse.
Ja kui puutute kokku ebavõrdsusega nagu
siis vastus on:
х πn, n ∈ Z
on haruldane jama, jah ...) Siin on vaja otsustada trigonomeetrilise ringi üle. Mida me vastavas teemas teeme.
Neile, kes on kangelaslikult neid ridu lugenud. Ma lihtsalt ei saa jätta hindamata teie titaanlikke pingutusi. Sulle boonus.)
Boonus:
Ärevust tekitavas lahingukeskkonnas valemeid kirjutades satuvad isegi akadeemiliselt paadunud nohikud sageli segadusse, kus πn, Ja kus 2π n. Siin on lihtne nipp. sisse kõigist valemid väärt πn. Välja arvatud ainus pöördkoosinusega valem. See seisab seal 2πn. Kaks pien. Märksõna - kaks. Sama valem sisaldab kaks märk alguses. Pluss ja miinus. Siin-seal - kaks.
Nii et kui sa kirjutasid kaks märk pöördkoosinuse ees, siis on lihtsam meeles pidada, mis lõpus on kaks pien. Ja juhtub isegi vastupidi. Jäta mehe märk vahele ± , jõuab lõpuni, kirjutab õigesti kaks pien, ja see tuleb mõistusele. Millegi ees kaks märk! Inimene naaseb algusesse, kuid ta parandab vea! Nagu nii.)
Kui teile meeldib see sait...
Muide, mul on teie jaoks veel paar huvitavat saiti.)
Saab harjutada näidete lahendamist ja teada saada oma taset. Kiire valideerimise testimine. Õppimine – huviga!)
saate tutvuda funktsioonide ja tuletistega.
Zakharova Ludmila Vladimirovna
MBOU "Keskkool nr 59" Barnaulis
matemaatika õpetaja
[e-postiga kaitstud]
№1 Lihtsamad trigonomeetrilised võrrandid
Sihtmärk: 1. Tuletage vormi lihtsaimate trigonomeetriliste võrrandite lahendite valemid sinx = a, cosx = a, tgx = a, ctgx = a;
2. Õppige valemite abil lahendama lihtsamaid trigonomeetrilisi võrrandeid.
Varustus: 1) Tabelid trigonomeetriliste funktsioonide y = graafikutega sinx, y = cosx, y = tgx, y = ctgx; 2) Trigonomeetriliste pöördfunktsioonide väärtuste tabel; 3) Valemite koondtabel lihtsamate trigonomeetriliste võrrandite lahendamiseks.
Loengu tunniplaan:
1 Võrrandi juurte valemite tuletamine
a) sinx = a,
b) cosx = a,
c) tgx = a,
d) ctgx = a.
2 ... Suuline frontaaltöö saadud valemite kinnistamiseks.
3 ... Kirjalik töö õpitud materjali kinnistamiseks
Tundide ajal.Algebras, geomeetrias, füüsikas ja teistes ainetes seisame silmitsi mitmesuguste ülesannetega, mille lahendamine on seotud võrrandite lahendamisega. Oleme uurinud trigonomeetriliste funktsioonide omadusi, mistõttu on loomulik pöörduda võrrandite poole, milles tundmatu sisaldub funktsioonide märgi all
Definitsioon: Vormi võrrandid sinx = a , cosx= a , tgx= a , ctgx= a nimetatakse lihtsaimateks trigonomeetrilisteks võrranditeks.
Väga oluline on õppida lahendama lihtsamaid trigonomeetrilisi võrrandeid, kuna kõik meetodid ja tehnikad mis tahes trigonomeetriliste võrrandite lahendamiseks on nende taandamine kõige lihtsamateks.
Alustame valemite tuletamisest, mis trigonomeetriliste võrrandite lahendamisel "aktiivselt" töötavad.
1.Vorrandid kujul sinx = a.
Lahendame võrrandi sinx = a graafiliselt. Selleks joonistame ühes koordinaatsüsteemis funktsioonide y = sinx ja y = graafikud a.
1) Kui a> 1 ja a patt x = a ei ole lahendusi, kuna sirgel ja sinusoidil pole ühiseid punkte.
2) Kui -1a a ületab sinusoidi lõpmatult palju kordi. See tähendab, et võrrand sinx = a on lõpmatult palju lahendusi.
Kuna siinuse periood on 2 
, siis võrrandi lahendamiseks sinx = a piisab, kui leida kõik lahendused mis tahes lõigul pikkusega 2.
Lahendades võrrandi [- / 2; / 2] arsiinuse x = definitsiooni järgi arcsin a, ja x = -arcsin a... Võttes arvesse funktsiooni y = sinx perioodilisust, saame järgmised avaldised
x = -artsin a+ 2n, n Z.
Mõlemat seeriat lahendusi saab kombineerida
X = (-1) n arcsin a+ n, nZ.
Järgmisel kolmel juhul eelistavad nad kasutada mitte üldist valemit, vaid lihtsamaid seoseid:
Kui a= -1, siis sin x = -1, x = - / 2 + 2n
Kui a= 1, siis sin x = 1, x = / 2 + 2n
Kui a = 0, siis sin x = 0. x = n,
Näide: lahendage võrrand sinx = 1/2.
Koostame lahenduste valemid x = arcsin 1/2 + 2n
X = - arcsin a + 2n
Arvutame väärtuse arcsin1/2. Asendage leitud väärtus lahendusvalemites
x = 5/6 + 2 n
või üldvalemiga
X = (-1) n arcsin 1/2 + n,
X = (-1) n / 6 + n,
2. Vormi võrrandid cosx = a.
Lahendame võrrandi cosx = a ka graafiliselt, joonistades funktsioonide y = cosx ja y = graafikud a.
1) Kui 1, siis võrrand cosx = a ei ole lahendusi, kuna graafikutel pole ühiseid punkte.
2) Kui -1 a cosx = a on lõpmatu arv lahendusi.
Leiame kõik lahendused cosx = a intervallil pikkusega 2, kuna koosinuse periood on 2.
Võrrandi lahendamisel arkosiini definitsiooni järgi on x = arcos a. Arvestades koosinusfunktsiooni paarsust, on võrrandi [-; 0] lahend x = -arcos a.
Seega võrrandi lahendid cosx = a x = + arcos a+ 2 n,
Kolmel juhul ei kasuta me üldist valemit, vaid lihtsamaid seoseid:
Kui a= -1, siis cosx = -1, x = - / 2 + 2n
Kui a= 1, siis cosx = 1, x = 2n,
Kui a = 0, siis cosx = 0. x = / 2 + n
Näide: lahendage võrrand cos x = 1/2,
Koostame lahenduste valemid x = kaared 1/2 + 2n
Arvutame väärtuse arccos 1/2.
Asendage leitud väärtus lahendusvalemites
X = + /3+ 2n, nZ.
Vormi võrrandid tgx = a.
Kuna puutuja periood on võrdne, siis selleks, et leida võrrandi kõik lahendid tgx = a, piisab, kui leida kõik lahendused mis tahes pikkuse intervallil. Arktangensi definitsiooni järgi on võrrandi (- / 2; / 2) lahend arktaan a. Võttes arvesse funktsiooni perioodi, saab kõik võrrandi lahendid kirjutada kujule
x = arctg a+ n, nZ.
Näide: Lahenda võrrand tg x = 3/3
Koostame valemi x = lahendamiseks arctan 3/3 + n, nZ.
Arvutame arktangensi väärtuse arctan 3/3 = / 6, siis
X = /6 + n, nZ.
Võrrandi lahendamise valemi tuletamine Koos tgx= a saab pakkuda õpilastele.
Näide.
Lahenda võrrand ctg x = 1.
x = arcсtg 1 + n, nZ,
X = /4 + n, nZ.
Uuritud materjali tulemusena saavad õpilased täita tabeli:
"Trigonomeetriliste võrrandite lahendamine."
võrrand
Harjutused õpitud materjali kinnistamiseks.
(Suuliselt) Milliseid kirjutatud võrrandeid saab lahendada valemitega:
a) x = (-1) n arcsin a+ n, nZ;
b) x = + arcos a + 2 n?
cos x = 2/2, tg x = 1, sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 ...
Millistel loetletud võrranditest pole lahendusi?
Lahendage võrrandid:
a) sin x = 0; e) sin x = 2/2; h) sin x = 2;
b) cos x = 2/2; f) cos x = -1/2; i) cos x = 1;
d) tg x = 3; g) ctg x = -1; j) tg x = 1/3.
3. Lahendage võrrandid:
a) sin 3x = 0; e) 2cos x = 1;
b) cos x / 2 = 1/2; f) 3 tan 3x = 1;
d) sin x / 4 = 1; g) 2cos (2x + / 5) = 3.
Nende võrrandite lahendamisel on kasulik kirja panna vormi võrrandite lahendamise reeglid patt v x = a, ja Koos patt v x = a, | a|1.
Patt v x = a, | a | 1.
v x = (-1) n arcsin a+ n, nZ,
x = (-1) n 1 / v arcsin a+ n / v, nZ.
Tunni tulemuste kokkuvõte:
Tänases tunnis oleme tuletanud valemid lihtsaimate trigonomeetriliste võrrandite lahendamiseks.
Lahti võetud näited lihtsamate trigonomeetriliste võrrandite lahendamisest.
Täitsime tabeli, mida kasutame võrrandite lahendamisel.
Kodutöö.
№2 Trigonomeetriliste võrrandite lahendamine
Sihtmärk: Uurida trigonomeetriliste võrrandite lahendamise meetodeid: 1) ruutvõrranditeks taandatavad 2) homogeenseteks trigonomeetrilisteks võrranditeks taandatavad.
Arendada õpilaste vaatlusoskust erinevate trigonomeetriliste võrrandite lahendamise meetodite kasutamisel.
Frontaalne töö õpilastega.
Millised on trigonomeetriliste võrrandite juurte valemid cos x = a, sin x = a, tgx = a, ctg x = a.
Lahendage võrrandid (suuliselt):
cos x = -1, sin x = 0, tgx = 0, ctg x = 1, cos x = 1,5, sin x = 0.
Otsige üles vead ja mõelge vigade põhjustele.
cos x = 1/2, x = +
/ 6 + 2k, k 
Z.
sin x = 3/2, x = / 3 + k, kZ.
tgx = / 4, x = 1 + k, kZ.
2. Uue materjali õppimine.
See õppetund hõlmab mõningaid kõige levinumaid trigonomeetriliste võrrandite lahendamise meetodeid.
Trigonomeetrilised võrrandid on taandatud ruutarvuks.
See klass võib sisaldada võrrandeid, mis sisaldavad ühte funktsiooni (siinus või koosinus) või ühe argumendi kahte funktsiooni, kuid üks neist taandatakse põhiliste trigonomeetriliste identiteetide abil teiseks.
Näiteks kui cosх sisaldub võrrandis paarisastmetes, siis asendame selle 1- sin 2 x, kui sin 2 x, siis asendame selle 1-cos 2 x-ga.
Näide.
Lahendage võrrand: 8 sin 2 x - 6sin x -5 = 0.
Lahendus: tähistame sin x = t, siis 8t 2 - 6t - 5 = 0,
D = 196,
T 1 = -1/2, t 2 = -5/4.
Teeme pöördmuutuse ja lahendame järgmised võrrandid.
X = (-1) k + 1/6 + k, kZ.
Kuna -5/4> 1, pole võrrandil juuri.
Vastus: x = (- 1) k + 1/6 + k, kZ.
Tugevdusharjutuste lahendus.
Lahenda võrrand:
1) 2sin 2 x + 3cos x = 0;
2) 5sin 2 x + 6cos x -6 = 0;
3) 2sin 2 x + 3cos 2 x = -2sin x;
4) 3 tg 2 x +2 tgx-1 = 0.
Homogeensed trigonomeetrilised võrrandid.
Definitsioon: 1) Vormi võrranda sinx + b cosx= 0, (a = 0, b = 0) nimetatakse esimese astme homogeenseks võrrandiks sin x ja cos x suhtes.
See võrrand lahendatakse, jagades selle mõlemad osad arvuga cosx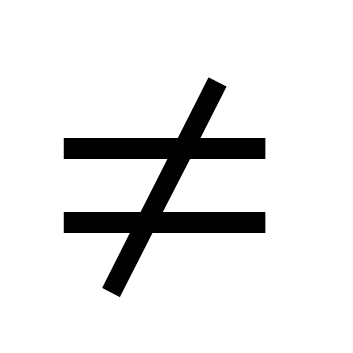 
0. Tulemuseks on võrrand atgx + b = 0.
2) Vormi võrranda patt 2 x + b sinx cosx + c cos 2 x =0 nimetatakse teise astme homogeenseks võrrandiks, kus a, b, c on suvalised arvud.
Kui a = 0, siis lahendatakse võrrand, jagades mõlemad osad arvuga sest 2x 0. Selle tulemusena saame võrrandi atg 2 x + btgx + c = 0.
Kommentaar: Vormi võrranda patt mx + b cos mx=0 või
a patt 2 mx + b patt mx cos mx + c cos 2 mx =0 on ka homogeensed. Nende lahendamiseks jagatakse võrrandi mõlemad pooled cos-iga mx=0 või cos 2 mx=0
3) Erinevaid võrrandeid saab taandada homogeenseteks võrranditeks, mis esialgu nii ei ole. Näiteks,patt 2 mx + b patt mx cos mx + c cos 2 mx = d, ja a sinx + b cosx= d. Nende võrrandite lahendamiseks peate korrutama parema küljega "Trigonomeetriline ühik" need. peal patt 2 x + cos 2 x ja sooritada matemaatilisi teisendusi.
Harjutused õpitud materjali konsolideerimiseks:
1) 2sin x- 3cos x = 0; 5) 4 sin 2 x - sin2x = 3;
2) sin 2x + cos2x = 0; 6) 3 sin 2 x + sinx cosx = 2 cos 2 x;
3) sin x + 3cos x = 0; 7) 3 sin 2 x- sinx cosx = 2;
4) sin 2 x -3 sinx cosx +2 cos 2 x = 0
3. Tunni tulemuste kokkuvõtte tegemine. Kodutöö.
Selles õppetükis võite sõltuvalt rühma valmisolekust kaaluda vormi võrrandite lahendamist a sin mx + b cos mx = c, kus a, b, c ei ole samal ajal võrdsed nulliga.
Tugevdavad harjutused:
1,3sin x + cos x = 2;
2.3sin 2x + cos 2x = 2;
3.sin x / 3 + cos x / 3 = 1;
4,12 sin x +5 cos x + 13 = 0.
№ 3 Trigonomeetriliste võrrandite lahendamine
Sihtmärk: 1) Uurige trigonomeetriliste võrrandite lahendamise meetodit faktoriseerimise teel; õppida lahendama trigonomeetrilisi võrrandeid kasutades erinevaid trigonomeetrilisi valemeid;
2) Kontrollige: õpilaste teadmisi lihtsamate trigonomeetriliste võrrandite lahendamise valemitest; oskus lahendada lihtsamaid trigonomeetrilisi võrrandeid.
Tunniplaan:
Kodutööde kontroll.
Matemaatiline diktaat.
Uue materjali õppimine.
Iseseisev töö.
Tunni tulemuste kokkuvõte. Kodutöö.
Tunni käik:
Kodutööde kontroll (trigonomeetriliste võrrandite lahendus on lühidalt kirjutatud tahvlile).
Matemaatiline diktaat.
IN 1
1. Milliseid võrrandeid nimetatakse lihtsaimateks trigonomeetrilisteks võrranditeks?
2. Mis on vormi võrrandi nimia sinx + b cosx = 0? Palun märkige viis selle lahendamiseks.
3.Kirjutage võrrandi juurte valem tgx = a(ctg x = a).
4. Kirjutage üles vormi võrrandite juurte valemid cosx = a, kus a=1, a=0, a=-1.
5. Kirjutage üles võrrandi juurte üldvalem sin x = a, | a|
6. Kuidas on vormi võrrandida cosx = b, | b|
2
1. Kirjutage üles võrrandite juurte valemid cosx = a,| a|
2. Kirjutage üles võrrandi juurte üldvalem
= a, | a|
3. Mis on vormi võrrandite nimetused sin x = a, tgx = a, sin x = a?
4. Kirjutage üles võrrandi juurte valemid sin x = a, kui a=1, a=0, a=-1.
5.Kuidas on vormi võrrandid patt a x = b, | b|
6. Milliseid võrrandeid nimetatakse teise astme homogeenseteks võrranditeks? Kuidas need lahendatakse?
Uue materjali õppimine.
Faktoring meetod.
Üks kõige sagedamini kasutatavaid meetodeid trigonomeetriliste võrrandite lahendamiseks on faktoriseerimise meetod.
Kui võrrandit f (x) = 0 saab esitada f 1 (x) f 2 (x) = 0, siis taandatakse ülesanne kahe võrrandi lahendamiseks f 1 (x) = 0, f 2 (x) = 0 .
(Õpilaste puhul on kasulik meeles pidada reeglit " Tegurite korrutis on null, kui vähemalt üks teguritest on null, samas kui teised on mõistlikud»)
Õpitava materjali konsolideerimine erineva keerukusega võrrandite lahendamise kaudu.
(sin x-1/2) (sin x + 1) = 0; 2) (cosx- 2/2) (sin x + 2/2) = 0; (ise)
3) sin 2 x + sin x cosx = 0; 4) sin 2 x - sin x = 0;
5) sin 2x - cosx = 0; 6) 4 cos 2 x -1 = 0; (Kahel viisil)
7) cosx + cos3x = 0; 8) sin 3x = sin 17x;
9) sin x + sin 2x + sin 3x = 0; 10) cos3x cos5x
11) sin x cos5x = sin 9x cos3x sin 2x sin 2x
12) 3 cosx sin x + cos 2 x = 0 (ise)
13) 2 cos 2 x - sin (x- / 2) + tgx tg (x + / 2) = 0.
Iseseisev töö.
Valik-1 Valik-2
1) 6 sin 2 x + 5sin x -1 = 0; 1) 3 cos 2 x + 2 cosx -5 = 0;
2) sin 2x - cos2x = 0; 2) 3 cos x / 2 - sin x / 2 = 0;
3) 5 sin 2 x + sin x cosx -2 cos 2 x = 2; 3) 4sin 2 x- sin x cosx + 7cos 2 x = 5;
4) sin x + sin5x = sin3x + sin7x; 4) sin x-sin 2x + sin 3x-sin 4x = 0;
5) sin x + cosx = 1. 5) sin x + cosx = 2.
8. Õppetunni kokkuvõtte tegemine. Kodutöö.
