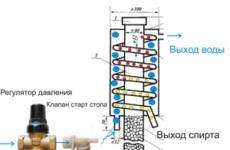
Anna esimerkkejä, mitä tasoja kutsutaan yhdensuuntaisiksi. Tasojen rinnakkaisuus: merkki, kunto. Yhdensuuntaiset tasot esimerkein

Tason sijainti avaruudessa määritetään:

• kolme pistettä, jotka eivät ole samalla viivalla;
• suora ja suoran ulkopuolelta otettu piste;
• kaksi leikkaavaa viivaa;
• kaksi yhdensuuntaista viivaa;
• litteä figuuri.

Tämän mukaisesti taso voidaan määrittää kaavioon:

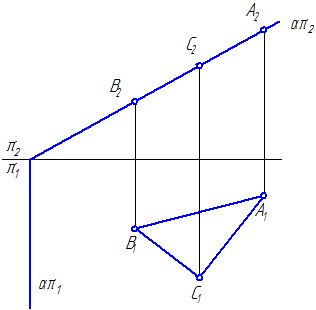
• kolmen pisteen projektiot, jotka eivät ole samalla suoralla (kuva 3.1, a);
• pisteen ja suoran projektiot (kuva 3.1,b);
• kahden leikkaavan suoran projektiot (kuva 3.1c);
• kahden yhdensuuntaisen suoran projektiot (kuva 3.1d);
• litteä hahmo (kuva 3.1, d);
• lentokoneen jäljet;
• tason suurimman kaltevuuden viiva.

Kuva 3.1 – Tasojen määrittelymenetelmät

Lentokone yleinen kanta on taso, joka ei ole yhdensuuntainen eikä kohtisuora mihinkään projektiotasoon nähden.

Lentokoneen perässä on suora, joka saadaan tietyn tason ja yhden projektiotason leikkauspisteestä.

Yleisellä koneella voi olla kolme jälkiä: vaakasuoraan – απ 1, edestä – απ 2 ja profiili – απ 3, jonka se muodostaa leikkaaessaan tunnettuja projektiotasoja: vaakasuuntainen π 1, frontaalinen π 2 ja profiili π 3 (kuva 3.2).

Kuva 3.2 – Yleistason jäljet

3.2. Osittainen lentokoneet

Osittainen taso– taso, joka on kohtisuorassa tai yhdensuuntainen projektiotasoon nähden.

Projektitasoon nähden kohtisuorassa olevaa tasoa kutsutaan projektioksi ja tälle projektiotasolle se projisoidaan suorana viivana.

Projektiotason ominaisuus: kaikilla ulkonevaan tasoon kuuluvilla pisteillä, viivoilla, litteillä hahmoilla on projektiot tason kaltevalla jäljellä(Kuva 3.3).

Kuva 3.3 – Edestä ulkoneva taso, joka sisältää: pisteet A, SISÄÄN, KANSSA; rivit AC, AB, Aurinko; kolmion taso ABC

Etuprojektiotaso – taso, joka on kohtisuorassa projektioiden etutasoon nähden(Kuva 3.4, a).

Vaakasuora projektiotaso – taso, joka on kohtisuorassa projektioiden vaakatasoon nähden(Kuva 3.4, b).

Profiilin projisointitaso – taso, joka on kohtisuorassa projektioiden profiilitasoon nähden.

Projektitasojen kanssa yhdensuuntaisia ​​tasoja kutsutaan tasaiset tasot tai kaksinkertaiset ulkonevat tasot.

Etutason taso – taso, joka on yhdensuuntainen projektioiden etutason kanssa(Kuva 3.4, c).

Vaakasuora taso – taso, joka on yhdensuuntainen projektioiden vaakatason kanssa(Kuva 3.4, d).

Tason profiilitaso – taso, joka on yhdensuuntainen projektioiden profiilitason kanssa(Kuva 3.4, e).

Kuva 3.4 – Kaaviot tietyn sijainnin tasoista

3.3. Piste ja suora tasossa. Pisteen ja suoran tason kuuluminen

Piste kuuluu tasoon, jos se kuuluu mihin tahansa tässä tasossa olevaan suoraan(Kuva 3.5).

Suora kuuluu tasoon, jos sillä on vähintään kaksi yhteistä pistettä tason kanssa(Kuva 3.6).

Kuva 3.5 – Pisteen kuuluminen tasoon

α = m // n

D∈ n⇒ D∈ α

Kuva 3.6 – Suoraan tasoon kuuluva

Harjoittele

Annettu taso, jonka määrittelee nelikulmio (Kuva 3.7, a). On tarpeen suorittaa yläosan vaakasuora projektio KANSSA.

A	b

Kuva 3.7 – Ratkaisu ongelmaan

Ratkaisu :

1. ABCD– tasainen nelikulmio, joka määrittää tason.
2. Piirretään siihen diagonaalit A.C. Ja BD(Kuva 3.7, b), jotka ovat leikkaavia suoria, jotka myös määrittelevät saman tason.
3. Leikkaavien viivojen kriteerin mukaan rakennamme vaakasuoran projektion näiden viivojen leikkauspisteestä - K sen tunnetun frontaalisen projektion mukaan: A 2 C 2 ∩ B 2 D 2 =K 2 .
4. Palautetaan projektioliitosviiva, kunnes se leikkaa suoran vaakaprojektion BD: diagonaaliprojektiossa B 1 D 1 rakennamme TO 1 .
5. Kautta A 1 TO 1 suoritamme diagonaalisen projektion A 1 KANSSA 1 .
6. Täysi pysähdys KANSSA 1 saadaan projektioliitäntälinjan kautta, kunnes se leikkaa laajennetun diagonaalin vaakaprojektion kanssa A 1 TO 1 .

3.4. Päätason linjat

Tasoon voidaan rakentaa ääretön määrä suoria, mutta tasossa on erityisiä suoria ns. koneen päälinjat (Kuva 3.8 – 3.11).

Suora taso tai yhdensuuntainen tason kanssa on suora viiva, joka sijaitsee tietyssä tasossa ja on yhdensuuntainen yhden projektiotason kanssa.

Vaakasuora tai vaakasuora tasoviiva h(ensimmäinen yhdensuuntaisuus) on suora viiva, joka sijaitsee tietyssä tasossa ja on yhdensuuntainen projektioiden vaakatason kanssa (π 1)(Kuva 3.8, a; 3.9).

Edessä tai etutason suora f(toinen yhdensuuntaisuus) on suora viiva, joka sijaitsee tietyssä tasossa ja on yhdensuuntainen projektioiden etutason kanssa (π 2)(Kuva 3.8, b; 3.10).

Tasoprofiiliviiva s(kolmas yhdensuuntaisuus) on suora viiva, joka sijaitsee tietyssä tasossa ja on yhdensuuntainen projektioiden profiilitason kanssa (π 3)(Kuva 3.8, c; 3.11).

Kuva 3.8 a – Tason vaakasuora viiva kolmion määrittelemässä tasossa

Kuva 3.8 b – Tason etuviiva kolmion määrittelemässä tasossa

Kuva 3.8 c – Tasoprofiiliviiva kolmion määrittelemässä tasossa

Kuva 3.9 – Tason vaakasuora viiva raitojen määrittelemässä tasossa

Kuva 3.10 – Tason etusuora raiteiden määrittelemässä tasossa

Kuva 3.11 – Tasoprofiiliviiva raiteiden määrittelemässä tasossa

3.5. Suoran ja tason keskinäinen sijainti

Tiettyyn tasoon nähden suora voi olla yhdensuuntainen ja sillä voi olla sen kanssa yhteinen piste, eli se leikkaa.

3.5.1. Suoran tason rinnakkaisuus

Merkki suoran tason yhdensuuntaisuudesta: suora on yhdensuuntainen tason kanssa, jos se on yhdensuuntainen minkä tahansa tähän tasoon kuuluvan suoran kanssa(Kuva 3.12).

Kuva 3.12 – Suoran tason yhdensuuntaisuus

3.5.2. Suoran leikkaus tason kanssa

Rakentaaksesi suoran ja yleisen tason leikkauspisteen (kuva 3.13), sinun on:

1. Päätä suoraan A aputasoon β (aputasoksi tulee valita tietyn sijainnin tasot);
2. Etsi aputason β leikkausviiva annetun tason α kanssa;
3. Etsi tietyn suoran leikkauspiste A tasojen leikkausviivan kanssa MN.

Kuva 3.13 – Suoran ja tason kohtauspisteen rakentaminen

Harjoittele

Annettu: suora AB yleinen sijainti, taso σ⊥π 1. (Kuva 3.14). Muodosta suoran leikkauspiste AB tasossa σ.

Ratkaisu :

1. Taso σ projisoi vaakasuunnassa, joten tason σ vaakasuora projektio on suora σ 1 (tason vaakasuuntainen jälki);
2. Piste TO täytyy kuulua linjaan AB ⇒ TO 1 ∈A 1 SISÄÄN 1 ja tietty taso σ ⇒ TO 1 ∈σ 1 siis, TO 1 sijaitsee projektioiden leikkauspisteessä A 1 SISÄÄN 1 ja σ1;
3. Pisteen edestä projektio TO löydämme projektioviestintälinjan kautta: TO 2 ∈A 2 SISÄÄN 2 .

Kuva 3.14 – Yleisen suoran leikkauspiste tietyn tason kanssa

Harjoittele

Annettu: taso σ = Δ ABC– yleinen asento, suora E.F.(Kuva 3.15).

On tarpeen rakentaa suoran leikkauspiste E.F. tasossa σ.

A	b

Kuva 3.15 – Suoran ja tason leikkauspiste

1. Päätetään suora viiva E.F. aputasoon, jota varten käytämme vaakasuoraan projisoivaa tasoa α (kuva 3.15, a);
2. Jos α⊥π 1, niin projektiotasolle π 1 taso α projisoidaan suoraksi viivaksi (tason απ 1 tai α 1 vaakasuora viiva), joka on sama kuin E 1 F 1 ;
3. Etsitään ulkonevan tason α leikkausviiva (1-2) tason σ kanssa (tarkastellaan ratkaisua vastaavaan ongelmaan);
4. Suora (1-2) ja määritetty suora E.F. sijaitsevat samassa tasossa α ja leikkaavat pisteen K.

Algoritmi ongelman ratkaisemiseksi (Kuva 3.15, b):

Kautta E.F. Piirretään aputaso α:

3.6. Näkyvyyden määritys kilpailevan pisteen menetelmällä

Tietyn suoran paikkaa arvioitaessa on tarpeen määrittää, mikä suoran piste sijaitsee lähempänä (edemmäs) meitä tarkkailijoina, kun tarkastellaan projektiotasoa π 1 tai π 2.

Pisteitä, jotka kuuluvat eri objekteihin ja joiden projektiot ovat toisella projektiotasolla samat (eli kaksi pistettä heijastetaan yhdeksi), kutsutaan kilpaileviksi tällä projektiotasolla..

Näkyvyys on määritettävä erikseen jokaisella projektiotasolla.

Näkyvyys π 2:lla (kuva 3.15)

Valitaan pisteillä π 2 kilpailevat pisteet – pisteet 3 ja 4. Olkoon piste 3∈ VS∈σ, kohta 4∈ E.F..

Pisteiden näkyvyyden määrittämiseksi projektiotasolla π 2 on tarpeen määrittää näiden pisteiden sijainti vaakasuuntaisella projektiotasolla, kun tarkastellaan pistettä π 2.

Näytön suunta kohti π 2 on esitetty nuolella.

Pisteiden 3 ja 4 vaakasuorista projektioista π 2:ta tarkasteltaessa on selvää, että piste 4 1 sijaitsee lähempänä havainnoijaa kuin 3 1.

4 1 ∈E 1 F 1 ⇒ 4∈E.F.⇒ kohdassa π 2 näkyy piste 4, joka sijaitsee suoralla E.F., siis suoraan E.F. tarkasteltavien kilpailevien pisteiden alueella sijaitsee σ-tason edessä ja on näkyvissä pisteeseen asti K

Näkyvyys kohdassa π 1

Näkyvyyden määrittämiseksi valitsemme pisteet, jotka kilpailevat π 1 -pisteillä 2 ja 5.

Pisteiden näkyvyyden määrittämiseksi projektiotasolla π 1 on tarpeen määrittää näiden pisteiden sijainti frontaaliprojektiotasolla, kun tarkastellaan pistettä π 1.

Näytön suunta kohti π 1 on esitetty nuolella.

Pisteiden 2 ja 5 frontaalisista projektioista π 1:tä tarkasteltaessa on selvää, että piste 2 2 sijaitsee lähempänä havainnoijaa kuin 5 2.

2 1 ∈A 2 SISÄÄN 2 ⇒ 2∈AB⇒ kohdassa π 1 näkyy piste 2, joka sijaitsee suoralla AB, siis suoraan E.F. tarkasteltavien kilpailevien pisteiden alueella sijaitsee tason σ alla ja on näkymätön pisteeseen asti K– suoran ja tason σ leikkauspisteet.

Näkyvä kahdesta kilpailevasta pisteestä on se, jonka "Z" ja/tai "Y" koordinaatit ovat suuremmat.

3.7. Suoraan tasoon nähden kohtisuora

Merkki suoran tason kohtisuorasta: suora on kohtisuorassa tasoa vastaan, jos se on kohtisuorassa kahta tietyssä tasossa olevaa leikkaavaa suoraa vastaan.

A	b

Kuva 3.16 – Tasoon nähden kohtisuoran suoran määrittäminen

Lause. Jos suora on kohtisuorassa tasoon nähden, niin kaaviossa: suoran vaakasuora projektio on kohtisuorassa tason vaakatason vaakaprojektioon nähden ja suoran etuprojektio on kohtisuorassa etuosa (kuva 3.16, b)

Lause todistetaan suoran kulman projektion lauseella erityistapauksessa.

Jos taso määritellään juovilla, niin tasoon nähden kohtisuorassa olevan suoran projektiot ovat kohtisuorassa tason vastaaviin jälkiin (Kuva 3.16, a).

Anna sen olla suora s kohtisuorassa tasoon σ=Δ ABC ja kulkee pisteen läpi K.

1. Muodostetaan vaaka- ja frontaaliviivat tasoon σ=Δ ABC : A-1∈σ; A-1//π 1 ; S-2∈σ; S-2//π 2 .
2. Palataan asiaan K kohtisuorassa tiettyyn tasoon nähden: p 1⊥h 1 Ja p2⊥f 2, tai p 1⊥απ 1 Ja p2⊥απ 2

3.8. Kahden tason suhteellinen sijainti

3.8.1. Tasojen rinnakkaisuus

Kaksi tasoa voivat olla yhdensuuntaisia ​​ja leikkaavia.

Kahden tason yhdensuuntaisuuden merkki: kaksi tasoa ovat keskenään yhdensuuntaisia, jos yhden tason kaksi leikkaavaa suoraa ovat vastaavasti yhdensuuntaisia ​​toisen tason kahden leikkaavan suoran kanssa.

Harjoittele

Yleinen sijaintitaso on annettu α=Δ ABC ja kausi F∉α (kuva 3.17).

Pisteen läpi F piirrä taso β yhdensuuntainen tason α kanssa.

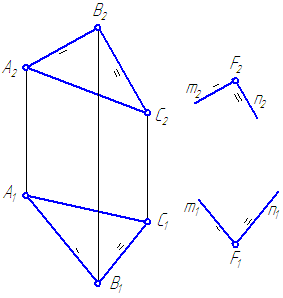
Kuva 3.17 – Tietyn tason kanssa yhdensuuntaisen tason rakentaminen

Ratkaisu :

Otetaan tason α leikkaaviksi suoriksi esimerkiksi kolmion AB ja BC sivut.

1. Pisteen läpi F teemme suoran m rinnakkain, esim. AB.
2. Pisteen läpi F tai minkä tahansa pisteen kautta m, piirrämme suoran viivan n rinnakkain, esim. Aurinko, ja m∩n = F.
3. β = m∩n ja β//α määritelmän mukaan.

3.8.2. Lentokoneiden risteys

Kahden tason leikkauksen tulos on suora. Mikä tahansa suora tasossa tai avaruudessa voidaan määrittää yksiselitteisesti kahdella pisteellä. Siksi kahden tason leikkausviivan rakentamiseksi sinun tulee löytää kaksi molemmille tasoille yhteistä pistettä ja sitten yhdistää ne.

Tarkastellaan esimerkkejä kahden tason leikkauspisteestä kohdassa eri tavoin heidän tehtävänsä: seuraavat; kolme pistettä, jotka eivät ole samalla viivalla; yhdensuuntaiset viivat; leikkaavat viivat jne.

Harjoittele

Kaksi tasoa α ja β määritellään jäljellä (kuva 3.18). Muodosta tasojen leikkausviiva.

Kuva 3.18 – Jälkien määrittelemien yleisten tasojen leikkauspiste

Menettely tasojen leikkausviivan muodostamiseksi:

1. Etsi vaakasuuntaisten jälkien leikkauspiste - tämä on piste M(hänen ennusteensa M 1 Ja M 2, kun M 1 =M, koska M – yksityinen piste, joka kuuluu tasoon π 1).
2. Etsi eturaitojen leikkauspiste - tämä on piste N(hänen ennusteensa N 1 ja N 2, kun N 2 = N, koska N – yksityinen piste, joka kuuluu tasoon π 2).
3. Muodosta tasojen leikkausviiva yhdistämällä tuloksena olevien samannimien pisteiden projektiot: M 1 N 1 ja M 2 N 2 .

MN– tasojen leikkausviiva.

Harjoittele

Annettu taso σ = Δ ABC, taso α – vaakasuoraan ulkoneva (α⊥π 1) ⇒α 1 – tason vaakasuora jälki (kuva 3.19).

Muodosta näiden tasojen leikkausviiva.

Ratkaisu :

Koska taso α leikkaa sivut AB Ja AC kolmio ABC, sitten leikkauspisteet K Ja L nämä sivut tason α kanssa ovat yhteisiä molemmille annetuille tasoille, mikä mahdollistaa ne yhdistämällä halutun leikkausviivan.

Pisteet löytyvät suorien viivojen leikkauspisteinä projektiotason kanssa: löydämme pisteiden vaakasuorat projektiot K Ja L, tuo on K 1 ja L 1, tietyn tason α vaakasuuntaisen jäljen (α 1) leikkauskohdassa sivujen Δ vaakaprojektioiden kanssa ABC: A 1 SISÄÄN 1 ja A 1 C 1 . Sitten, käyttämällä projektioviestintälinjoja, löydämme näiden pisteiden frontaaliset projektiot K2 Ja L 2 suorien viivojen etuprojektiossa AB Ja AC. Yhdistetään samannimiset projektiot: K 1 ja L 1 ; K2 Ja L 2. Piirretään annettujen tasojen leikkausviiva.

Algoritmi ongelman ratkaisemiseksi:

KL– leikkausviiva Δ ABC ja σ (α∩σ = KL).

Kuva 3.19 – Yleis- ja erityistasojen leikkauspiste

Harjoittele

Annetut tasot α = m//n ja taso β = Δ ABC(Kuva 3.20).

Muodosta annettujen tasojen leikkausviiva.

Ratkaisu :

1. Molemmille annetuille tasoille yhteisten pisteiden löytämiseksi ja tasojen α ja β leikkausviivan määrittämiseksi on käytettävä tietyn sijainnin aputasoja.
2. Tällaisiksi tasoiksi valitsemme kaksi aputasoa tietyllä paikalla, esimerkiksi: σ // τ; σ⊥π2; τ⊥π 2 .
3. Äskettäin käyttöönotetut tasot leikkaavat jokaisen annetuista tasoista α ja β toistensa suuntaisia ​​suoria pitkin, koska σ // τ:

— tasojen α, σ ja τ leikkaustulos ovat suoria viivoja (4-5) ja (6-7);

— tasojen β, σ ja τ leikkaustulos ovat suoria viivoja (3-2) ja (1-8).

1. Viivat (4-5) ja (3-2) sijaitsevat σ-tasolla; heidän leikkauspisteensä M on samanaikaisesti tasoissa α ja β, eli näiden tasojen leikkaussuoralla linjalla;
2. Samalla tavalla löydämme pointin N, yhteinen α- ja β-tasoille.
3. Yhdistää pisteet M Ja N, muodostetaan tasojen α ja β leikkaussuora.

Kuva 3.20 – Kahden tason leikkauspiste yleisessä asennossa (yleinen tapaus)

Algoritmi ongelman ratkaisemiseksi:

Harjoittele

Annetut tasot α = Δ ABC ja β = a//b. Muodosta annettujen tasojen leikkausviiva (kuva 3.21).

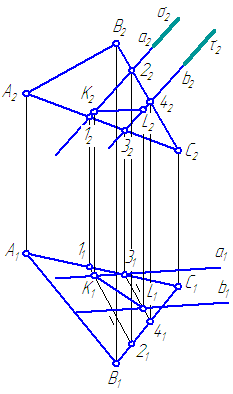
Kuva 3.21 Tasonleikkaustehtävän ratkaisu

Ratkaisu :

Käytetään tietyn sijainnin aputasoa. Otetaan ne käyttöön niin, että rakenteiden lukumäärä vähenee. Esitetään esimerkiksi taso σ⊥π 2 sulkemalla sisään suora a aputasoon σ (σ∈ a). Taso σ leikkaa tason α suoraa (1-2) pitkin ja σ∩β= A. Siksi (1-2)∩ A=K.

Piste TO kuuluu molemmille tasoille α ja β.

Siksi pointti K, on yksi vaadituista pisteistä, jonka kautta annettujen tasojen α ja β leikkausviiva kulkee.

Löytääksemme toisen pisteen, joka kuuluu α:n ja β:n leikkausviivaan, päätämme suoran b aputasoon τ⊥π 2 (τ∈ b).

Yhdistää pisteet K Ja L, saadaan tasojen α ja β leikkaussuora.

3.8.3. Toisiaan kohtisuorat tasot

Tasot ovat keskenään kohtisuorassa, jos yksi niistä kulkee kohtisuoran läpi toiseen.

Harjoittele

Annettu taso σ⊥π 2 ja suora yleisasemassa – DE(Kuva 3.22)

Pakollinen rakentamaan läpi DE taso τ⊥σ.

Ratkaisu .

Piirretään kohtisuora CD tasoon σ – C 2 D 2 ⊥σ 2 (perustuu ).

Kuva 3.22 – Tiettyyn tasoon nähden kohtisuoran tason rakentaminen

Oikean kulman projektiolauseen mukaan C 1 D 1 on oltava yhdensuuntainen projektioakselin kanssa. Leikkaavat linjat CD∩DE määrittele taso τ. Joten, τ⊥σ.

Samanlainen päättely yleisen tason tapauksessa.

Harjoittele

Annettu taso α = Δ ABC ja kausi Kα-tason ulkopuolella.

On rakennettava pisteen läpi kulkeva taso β⊥α K.

Ratkaisualgoritmi(Kuva 3.23):

1. Rakennetaan vaakasuora viiva h ja edessä f tietyssä tasossa α = Δ ABC;
2. Pisteen läpi K piirretään kohtisuora b tasoon α (myös kohtisuorassa tasolauseeseen nähden: jos suora on kohtisuorassa tasoon nähden, niin sen projektiot ovat kohtisuorassa tasossa olevien vaaka- ja etulinjojen kaltevia projektioita vastaan:b 2⊥f 2; b 1⊥h 1;
3. Määrittelemme tason β millä tahansa tavalla, esimerkiksi β = a∩b, jolloin muodostetaan taso, joka on kohtisuorassa annettua tasoa vastaan: α⊥β.

Kuva 3.23 – Tiettyyn Δ:hen nähden kohtisuoran tason rakentaminen ABC

3.9. Ongelmia ratkaista itsenäisesti

1. Annettu taso α = m//n(Kuva 3.24). On tiedossa, että K∈α.

Muodosta pisteen frontaaliprojektio TO.

Kuva 3.24

2. Muodosta janan antaman suoran jäljet C.B., ja tunnista kvadrantit, joiden läpi se kulkee (Kuva 3.25).

Kuva 3.25

3. Muodosta tasoon α⊥π 2 kuuluvan neliön projektiot, jos sen diagonaali MN//π 2 (kuva 3.26).

Kuva 3.26

4. Muodosta suorakulmio ABCD isomman puolen kanssa Aurinko suoralla linjalla m, sillä ehdolla, että sen sivujen suhde on 2 (kuva 3.27).

Kuva 3.27

5. Annettu taso α= a//b(Kuva 3.28). Muodosta taso β yhdensuuntainen tason α kanssa ja etäällä siitä 20 mm etäisyydellä.

Kuva 3.28

6. Annettu taso α=∆ ABC ja kausi D D taso β⊥α ja β⊥π 1 .

7. Annettu taso α=∆ ABC ja kausi D ulos koneesta. Rakenna pisteen läpi D suoraan DE//α ja DE//π 1 .

Tasojen rinnakkaisuus. Jos yhden tason kaksi leikkaavaa suoraa ovat vastaavasti yhdensuuntaisia ​​toisen tason kahden leikkaavan suoran kanssa, niin nämä tasot ovat yhdensuuntaisia.
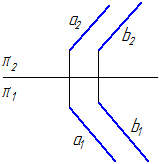
Todiste. Antaa a Ja b- lentotiedot, a 1 Ja a 2– suorat viivat tasossa a, leikkaa pisteessä A, b 1 Ja b 2 vastaavasti niiden kanssa samansuuntaiset viivat tasossa b. Oletetaan, että lentokoneet a Ja b eivät ole yhdensuuntaisia, eli ne leikkaavat jotakin suoraa pitkin Kanssa. Suoraan A 1 on yhdensuuntainen viivan kanssa b 1, mikä tarkoittaa, että se on yhdensuuntainen itse tason kanssa b(merkki yhdensuuntaisuudesta suoran ja tason välillä). Suoraan A 2 on yhdensuuntainen viivan kanssa b 2, tämä tarkoittaa, että se on yhdensuuntainen itse tason kanssa b(merkki yhdensuuntaisuudesta suoran ja tason välillä). Suoraan Kanssa kuuluu koneeseen a, mikä tarkoittaa ainakin yhtä suorista viivoista a 1 tai a 2 leikkaa linjan Kanssa, eli sillä on yhteinen pointti sen kanssa. Mutta suoraan Kanssa kuuluu myös koneeseen b, mikä tarkoittaa rajan ylittämistä Kanssa, suoraan a 1 tai a 2 leikkaa koneen b, joka ei voi olla, koska ne ovat suoria a 1 Ja a 2 yhdensuuntainen tason kanssa b. Tästä seuraa, että lentokoneet a Ja b eivät leikkaa, eli ne ovat yhdensuuntaisia.

Lause 1 . Jos kaksi yhdensuuntaista tasoa leikkaavat kolmasosaa, leikkaussuorat ovat yhdensuuntaiset.
Todiste. Antaa a Ja b- yhdensuuntaiset tasot ja g - niitä leikkaava kone. Lentokone a leikattu lentokoneen kanssa g suorassa linjassa A. Lentokone b leikattu lentokoneen kanssa g suorassa linjassa b. Risteyslinjat A Ja b makaa samassa tasossa g ja siksi ne voivat olla joko leikkaavia tai yhdensuuntaisia ​​suoria. Mutta koska ne kuuluvat kahteen yhdensuuntaiseen tasoon, niillä ei voi olla yhteisiä pisteitä. Siksi ne ovat rinnakkaisia.

Lause 2. Kahden yhdensuuntaisen tason välissä olevat yhdensuuntaisten viivojen segmentit ovat yhtä suuret.
Todiste. Antaa a Ja b- yhdensuuntaiset tasot ja A Ja b- niitä leikkaavat yhdensuuntaiset suorat. Suorien linjojen kautta A Ja b me suoritamme kone g (nämä viivat ovat yhdensuuntaisia, mikä tarkoittaa määrittää tason ja vain yhden). Lentokone a leikattu lentokoneen kanssa g suorassa AB . Lentokone b leikattu lentokoneen kanssa g pitkin suoraa SD. Edellisen lauseen mukaan suora Kanssa yhdensuuntainen linjan kanssa d. Suoraan A,b, AB Ja SD kuuluvat koneeseen g.Näiden viivojen rajoittama nelikulmio on suunnikkaampi (sillä on vastakkaiset puolet rinnakkain). Ja koska tämä on suunnikas, niin sen vastakkaiset sivut ovat yhtä suuret, eli AD = BC

Tarkastellaan tasojen yhdensuuntaisuuden suhdetta, sen ominaisuuksia ja sovelluksia.

Visuaalinen esitys näiden kahden sijainnista

Tasot saadaan mallintamalla käyttämällä huoneen viereisten seinien, katon ja lattian pintojen tasoja, kerrossängyt, kaksi paperiarkkia kiinni

taikurit jne. (kuvat 242–244).

Vaikka eri tasojen suhteelliselle sijainnille on ääretön määrä vaihtoehtoja, jotta pystymme määrittämään ja luonnehtimaan, mitä kulmien ja etäisyyksien mittauksia tulevaisuudessa käytetään, keskitymme ensin niihin, joissa luokittelu (sekä suorat tasojen kanssa ) perustuu niiden yhteisten pisteiden määrään.

1. Kahdella tasolla on vähintään kolme yhteistä pistettä, jotka eivät ole samalla suoralla. Tällaiset tasot osuvat yhteen (aksiooma C 2, §7).

2. Kahden tason yhteiset pisteet sijaitsevat yhdellä suoralla, joka on näiden tasojen leikkausviiva (aksiooma C 3, §7). Tällaiset tasot leikkaavat.

3. Molemmilla tasoilla ei ole yhteisiä pisteitä.

SISÄÄN tässä tapauksessa niitä kutsutaan rinnakkain-

Kahta tasoa kutsutaan rinnakkaiseksi, jos niillä ei ole yhteisiä pisteitä.

Tasojen yhdensuuntaisuus ilmaistaan ​​merkillä ||: α || β.

Kuten aina, esittelyssä geometrisia käsitteitä nousi

Niiden olemassaolossa ei ole ongelmaa. Leikkauksen olemassaolo

Xia-koneet ovat ominaispiirre tilaa,

ja olemme käyttäneet tätä jo monta kertaa. Vähemmän ilmeinen on

Yhdensuuntaisten tasojen olemassaolo paljastuu. Ei ole

epäilee, että esimerkiksi vastakkaisten kaavioiden tasot

Kuutiot ovat yhdensuuntaisia, eli ne eivät leikkaa. Mutta suoraan

Itse asiassa määritelmän mukaan tätä ei voida vahvistaa. Ratkaisua varten

esitettävän kysymyksen ymmärtäminen sekä muut siihen liittyvät asiat

tasojen yhdensuuntaisuus, on oltava samansuuntaisuuden merkki.

Merkin etsimiseksi on suositeltavaa harkita lentokonetta,

"kudottu" suorista linjoista. On selvää, että jokainen suora on yksi

yhdensuuntaisten tasojen on oltava yhdensuuntaisia ​​toisen kanssa.

Muuten koneilla on yhteinen piste. Tarpeeksi

Onko taso β täsmälleen samansuuntainen saman suoran α kanssa

niin että tasot α ja β ovat yhdensuuntaiset? Ehdottomasti

mutta ei (perustele tämä!). Käytännön kokemus osoittaa sen

kaksi tällaista leikkaavaa suoraa riittää. Varmistaa

mastossa on maanpinnan suuntainen taso, aseta se vain

Jos tasot ovat yhdensuuntaisia ​​toisen tason kanssa, niin nämä tasot ovat yhdensuuntaisia.

 Olkoot tason α leikkaavat suorat a ja b yhdensuuntaiset tason β kanssa. Osoitetaan ristiriidalla, että tasot α ja β ovat yhdensuuntaiset. Tätä varten oletetaan, että tasot α ja β leikkaavat suoraa viivaa pitkin

t (kuva 246). Suorat a ja b eivät voi leikata suoraa t ehdon mukaan. Kuitenkin tasossa α vedetään yhden pisteen läpi kaksi suoraa, jotka eivät leikkaa suoraa m, eli ovat sen suuntaisia. Tämä on ristiriita

ja suorittaa lauseen todistuksen.

Tasojen yhdensuuntaisuuden merkkiä käytetään vaakasuoraan sijoitettaessa litteät mallit (betonilaatat, lattia, goniometrilaitteiden kiekko jne.) käyttämällä kahta tasoa, jotka on sijoitettu rakenteen tasoon risteäville suorille viivoille. Tämän ominaisuuden perusteella on mahdollista rakentaa tämän kanssa yhdensuuntainen taso.

Tehtävä 1. Piirrä tietyn tason ulkopuolella olevan pisteen kautta taso, joka on yhdensuuntainen annetun tason kanssa.

 Olkoon taso β ja tason ulkopuolella oleva piste M (kuva 247, a). Piirretään pisteen M kautta kaksi leikkaavaa suoraa a ja b, jotka ovat yhdensuuntaisia ​​tason β kanssa. Tätä varten sinun on otettava kaksi leikkaavaa suoraa c ja d β-tasossa (kuva 247, b). Vedä sitten pisteen M kautta viivat a ja b, jotka ovat samansuuntaisia ​​suorien c ja d kanssa.

mutta (kuva 247, c).

Leikkaavat suorat a ja b yhdensuuntainen tason β kanssa, perustuen suoran ja tason yhdensuuntaisuuteen (Lause 1 §11). Ne määrittelevät yksiselitteisesti tason α. Todistetun kriteerin mukaan α || β.

Esimerkki 1. Kun on annettu kuutio ABCDA 1 B 1 C 1 D 1, pisteet M, N, P ovat reunojen BC, B 1 C 1 ja A 1 D 1 keskipisteitä. Asentaa keskinäinen järjestely tasot: 1) АВВ 1 ja PNM; 2) NMA ja A1C1C; 3) A 1 NM

ja PC1 C; 4) MAD 1 ja DB 1 C.

 1) Tasot ABB 1 ja PNM (kuva 248) ovat yhdensuuntaisia, perustuen tasojen yhdensuuntaisuuteen (Lause 1). Suorat PN ja NM leikkaavat ja ovat yhdensuuntaisia ​​tason ABB 1 kanssa, perustuen suoran ja tason yhdensuuntaisuuteen (Lause 1 §11), koska janat PN ja NM yhdistävät neliöiden vastakkaisten sivujen keskipisteet. , joten ne ovat yhdensuuntaiset neliöiden sivujen kanssa:

РN || A 1 B 1 , NM || B 1 B.

2) Tasot NMA ja A 1 C 1 C leikkaavat suoraa AA 1 pitkin (kuva 249). Itse asiassa suorat AA 1 ja CC 1 ovat yhdensuuntaisia, perustuen suorien (AA 1 || ВB 1, ВB 1 || СC 1) yhdensuuntaisuuteen. Siksi suora AA 1 on tasossa A 1 C 1 C. Myös suoran AA 1 kuuluminen NMA-tasoon on perusteltua.

3) Tasot A 1 NM ja PC 1 C (kuva 250) ovat yhdensuuntaisia, perustuen tasojen yhdensuuntaisuuteen. Todellakin, NM || C1C. Tästä syystä suora NM on yhdensuuntainen tason PC 1 C kanssa. Janat PC 1 ja A 1 N ovat myös yhdensuuntaisia, koska nelikulmio PC 1 NA 1 on suunnikas (A 1 P || NC 1, A 1 P = NC 1). Siten suora A 1 N on yhdensuuntainen tason PC 1 C kanssa. Suorat A 1 N ja NM leikkaavat.

4) Tasot MAD 1 ja DB 1 C leikkaavat (kuva 251). Vaikka niiden leikkausviivaa ei ole helppo rakentaa, ei ole vaikeaa osoittaa tämän suoran yhtä pistettä. Todellakin, suorat A 1 D ja B 1 C ovat yhdensuuntaisia, koska nelikulmio A 1 B 1 CD on suunnikas (A 1 B 1 = AB = CD, A 1 B 1 || AB, AB || CD). Siksi suora A 1 D kuuluu tasoon DB 1 C. Suorat A 1 D ja AD 1 leikkaavat pisteessä, joka on yhteinen tasoille MAD 1 ja DB 1 C.

Jos yhden tason kaksi leikkaavaa suoraa ovat vastaavasti yhdensuuntaisia ​​toisen tason kahden suoran kanssa, nämä tasot ovat yhdensuuntaisia.

Käyttämällä suoran ja tason yhdensuuntaisuuskriteeriä (Lause 1 §11) on helppo todeta, että Lauseen 1 ehto seuraa Lauseen 1 ehdoista. Lauseen soveltaminen käänteisesti yhdensuuntaisuuden kriteeriin suora ja taso (Lause 2 §11) täydentää lauseiden 1 ja 1 ′ ehtojen vastaavuuden perustelun.

Luonnollisesti herää kysymys tehtävässä 1 esitetyn rakenteen ainutlaatuisuudesta. Koska joudumme käyttämään tätä ominaisuutta useammin kuin kerran, korostamme sen erillisenä lauseena. Katsotaanpa kuitenkin ensin toista lausuntoa.

Lause 2 (kahden yhdensuuntaisen tason ja kolmannen leikkauspisteestä).

Jos kaksi yhdensuuntaista tasoa leikkaa kolmas taso, niin tasojen leikkausviivat ovat yhdensuuntaiset.

 Olkoon yhdensuuntaiset tasot α, β ja niitä leikkaava taso γ (kuva 252). Merkitään leikkausviivat

a:n ja b:n kautta. Nämä suorat sijaitsevat γ-tasossa eivätkä leikkaa, koska α- ja β-tasoilla ei ole yhteisiä pisteitä. Siis suoraan

a ja b ovat yhdensuuntaiset.

Lause 3 (tämän kanssa yhdensuuntaisen tason olemassaolosta ja ainutlaatuisuudesta).

Tietyn tason ulkopuolella sijaitsevan pisteen kautta voidaan piirtää yksi taso, joka on yhdensuuntainen annetun tason kanssa.

 Tällaisen tason rakentaminen suoritettiin tehtävässä 1. Todistamme rakenteen ainutlaatuisuuden ristiriitaisesti. Oletetaan, että pisteen M läpi piirretään kaksi eri tasoa α ja γ, pa-

yhdensuuntaiset tasot β (kuva 253), ja suora t on niiden leikkausviiva. Piirretään pisteen M läpi taso δ, joka leikkaa suoran

m ja β-taso (miten tämä voidaan tehdä?). Merkitään a:lla ja b:llä

tason δ leikkausviiva tasojen α ja γ kanssa ja c:n kautta - tasojen δ ja β leikkausviiva (kuva 253). Lauseen 2 mukaan ja || Kanssa

ja b || Kanssa. Eli δ-tasossa läpi

piste M ohittaa kaksi suoraa, jotka ovat yhdensuuntaisia ​​suoran c kanssa. Ristiriita osoittaa, että olettamus on väärä.

Tasojen yhdensuuntaisuuden suhteella on useita ominaisuuksia, joilla on analogeja planimetriassa.

Lause 4 (yhdensuuntaisten suorien segmenteistä yhdensuuntaisten tasojen välillä).

Yhdensuuntaisten tasojen leikkaamat yhdensuuntaisten viivojen segmentit ovat keskenään yhtä suuret.

 Olkoon kaksi yhdensuuntaista tasoa α ja β sekä segmenttejä AB

ja CD rinnakkaisten suorien a ja d, jotka on leikattu näillä tasoilla (kuva 254, a). Piirretään taso γ suorien a ja d kautta (kuva 254, b). Se leikkaa tasot α ja β suoria viivoja AC ja BD pitkin, jotka Lauseen 2 mukaan ovat yhdensuuntaiset. Siksi nelikulmio ABCD on suunnikkaampi, jonka vastakkaiset sivut AC ja BD ovat yhtä suuret.

Yllä olevasta ominaisuudesta seuraa, että jos piirrämme tason kaikista pisteistä

Tason toisella puolella on samanpituisia yhdensuuntaisia ​​segmenttejä, jolloin näiden segmenttien päät muodostavat kaksi yhdensuuntaista tasoa. Juuri tähän ominaisuuteen perustuu suuntaissärmiön rakentaminen segmenttien kerrostamalla (kuva 255).

Lause 5 (tasojen yhdensuuntaisuusrelaation transitiivisuudesta).

Jos kumpikin kahdesta tasosta on yhdensuuntainen kolmannen kanssa, niin nämä kaksi tasoa ovat yhdensuuntaisia ​​toistensa kanssa.

 Olkoot tasot α ja β yhdensuuntaiset tason γ kanssa. Oletetaan, että

α ja β eivät ole yhdensuuntaisia. Tällöin tasoilla α ja β on yhteinen piste, ja tämän pisteen kautta kulkee kaksi erilaista tasoa, jotka ovat yhdensuuntaisia ​​tason γ kanssa, mikä on ristiriidassa Lauseen 3 kanssa. Siksi tasoilla α ja β ei ole yhteisiä pisteitä, eli ne ovat yhdensuuntaisia. .

Lause 5 on toinen merkki tasojen yhdensuuntaisuudesta. Sitä käytetään laajasti sekä geometriassa että käytännön toiminnassa. Esimerkiksi sisään monikerroksinen rakennus lattia- ja kattotasojen yhdensuuntaisuus kussakin kerroksessa takaa niiden yhdensuuntaisuuden eri kerroksissa.

Tehtävä 2. Osoita, että jos suora a leikkaa tason α, niin se leikkaa myös jokaisen tason α kanssa yhdensuuntaisen tason.

 Olkoot tasot α ja β yhdensuuntaiset ja suoraviivainen pisteessä A leikkaava taso α. Osoittakaamme, että se leikkaa myös tason

β. Oletetaan, että näin ei ole. Tällöin suora a on yhdensuuntainen tason β kanssa. Piirretään taso γ suoran a kautta ja tason β mielivaltainen piste (kuva 256).

Tämä taso leikkaa yhdensuuntaiset tasot α ja β suoria b ja c pitkin. Yhteistyö

Lauseen 2 mukaan, b || c, eli γ-tasossa kaksi suoraa a ja b kulkevat pisteen A kautta, yhdensuuntaisesti suoran c kanssa . Tämä ristiriita vahvistaa väitteen.

Yritä itse todistaa, että jos taso α leikkaa tason β, niin se leikkaa myös jokaisen tason β kanssa yhdensuuntaisen tason.

Esimerkki 2. Tetraedrin ABCD pisteet K, F, E ovat reunojen DA, DC, DB keskipisteitä ja M ja P ovat pintojen ABD ja BCD massakeskuksia, vastaavasti.

1) Määritä tasojen KEF ja ABC suhteellinen sijainti;

DEF ja ABC.

2) Muodosta AFB- ja KEC-tasojen leikkausviiva.

3) Etsi tetraedrin poikkileikkauspinta-ala tason ABD kanssa yhdensuuntaisella ja pisteen P kautta kulkevalla tasolla, jos tetraedrin kaikki reunat ovat yhtä suuret kuin a.

 Tehdään piirustus, joka täyttää ehdon (Kuva 257, a). 1) Tasot KEF ja ABC ovat yhdensuuntaiset, perustuen tasojen yhdensuuntaisuuteen (Lause 1'): KEF-tason leikkaavat suorat KE ja KF ovat yhdensuuntaisia ​​ABC-tason leikkaavien suorien AB ja AC kanssa ( vastaavan keskiviivat

olemassa olevat kolmiot).

Tasot DEF ja ABC leikkaavat suoraa BC:tä pitkin, koska suora BC kuuluu molempiin tasoihin, eivätkä ne voi yhtyä - pisteet A, B, C, D eivät ole samassa tasossa.

2) Taso AFB leikkaa tason KEC pisteen P sisältävää suoraa pitkin, koska näissä tasoissa olevat suorat CE ja BF ovat tasossa BCD ja leikkaavat pisteessä P. Toinen piste on suorien AF ja CK leikkauspiste Q ACD-tasossa (kuva 257, b). Ilmeisesti tämä piste on ACD-pinnan massakeskus. Vaadittu leikkauspiste on linja PQ.

3) Muodosta ehdossa määritetty leikkaus käyttämällä tasojen yhdensuuntaisuuden merkkiä. Piirretään suoria kohtien P ja Q kautta samansuuntaisia ​​suoria DB ja DA (Kuva 257, c). Nämä suorat leikkaavat janan CD pisteessä L. Jälkimmäinen seuraa kolmion massakeskipisteen ominaisuudesta - se jakaa kolmion mediaanit suhteessa 2:1, laskettuna kärjestä. On vielä sovellettava Thaleen lausetta. Siten PLQ- ja BDA-tasot ovat yhdensuuntaiset. Tarvittava osa on kolmio LSN.

Kolmiot BCD ja SCL ovat rakenteeltaan samanlaisia ​​samankaltaisuuskertoimella CE CP = 3 2 . Siksi LS = 3 2 BD. Samanlainen kuin perustettu

yhtäläisyydet lisätään: LN = 3 2 AD, NS = 3 2 AB. Tästä seuraa, että kolmiot LSN ja ABD ovat samanlaisia ​​samankaltaisuuskertoimella 3 2. Samankaltaisten kolmioiden pinta-alojen ominaisuuksien mukaan

S LNS = 4 9 S ABD . On vielä löydettävä kolmion ABD pinta-ala. Tekijä-

koska ehdon mukaan tetraedrin kaikki reunat ovat yhtä suuria kuin a, niin S ABD = 4 3 a 2.

Vaadittu pinta-ala on 3 1 3 a 2 .

On syytä huomata, että vastaus riippuu vain kasvojen ABD-alueesta. Siksi kaikkien reunojen yhtäläisyys on vain keino löytää tämä alue. Näin ollen tämä ongelma voidaan yleistää huomattavasti.

Vastaus. 1) KEF || ABC ; 3) 3 1 3 a 2 .

 Testikysymykset

1. Onko totta, että kaksi tasoa ovat yhdensuuntaisia, jos jokainen yhdessä tasossa oleva suora on yhdensuuntainen toisen tason kanssa?

2. Tasot α ja β ovat yhdensuuntaiset. Onko näissä tasoissa vinoja viivoja?

3. Kolmion kaksi sivua ovat yhdensuuntaisia ​​tietyn tason kanssa. Onko kolmion kolmas sivu yhdensuuntainen tämän tason kanssa?

4. Suunnikkaan kaksi sivua ovat yhdensuuntaisia ​​tietyn tason kanssa. Onko totta, että suunnikkaan taso on yhdensuuntainen annetun tason kanssa?

5. Voivatko kahden samansuuntaisten tasojen leikkaaman suoran janat olla eriarvoisia?

6. Voiko kuution poikkileikkaus olla tasakylkinen puolisuunnikkaan muotoinen? Voiko kuution poikkileikkaus olla säännöllinen viisikulmio? Onko totta, että kaksi saman suoran suuntaista tasoa ovat yhdensuuntaisia ​​toistensa kanssa?

Tasojen α ja β leikkausviivat tason γ kanssa ovat yhdensuuntaiset toistensa kanssa. Ovatko tasot α ja β yhdensuuntaiset?

Voivatko kuution kolme sivua olla samansuuntaisia ​​saman tason kanssa?

Graafiset harjoitukset

1. Kuvassa 258 on esitetty kuutio ABCDA 1 B 1 C 1 D 1, pisteet M, N, K, L, P ovat vastaavien reunojen keskipisteitä. Täytä taulukko annetun esimerkin mukaisesti valitsemalla α- ja β-tasojen tarvittava sijainti.

Keskinäinen

sijainti

α || β α = β

α × β α || β α = β

2. Kuvassa 259 esittää tetraedrin ABCD, pisteet K, F, M, N, Q ovat vastaavien reunojen keskipisteitä. Ole hyvä ja osoita:

1) pisteen K kautta kulkeva taso, joka on yhdensuuntainen tason ABC kanssa;

2) taso, joka kulkee linjan BD kautta yhdensuuntaisesti tason MNQ kanssa.

3. Määritä, mikä on kuvion kolmen pisteen kautta kulkevan tason leikkaus.

kah 260, a)–e) ja 261, a)–d).

4. Rakenna piirustus annettujen tietojen perusteella.

1) Yhdellä kahdesta yhdensuuntaisesta tasosta olevasta suunnikkaan ABCD kärjestä piirretään yhdensuuntaiset suorat, jotka leikkaavat toisen tason pisteissä A 1 , B 1 , C 1 , D 1 , vastaavasti.

2) Kolmio A 1 B 1 C 1 on kolmion ABC projektio sen suuntaiselle tasolle α. Piste M on auringon keskipiste, M 1 on pisteen M projektio α-tasolle.

207. Kuutiossa ABCDA 1 B 1 C 1 D 1 pisteet O, O 1 ovat pintojen ABCD ja A 1 B 1 C 1 D 1 keskipisteitä, M on reunan AB keskipiste.

1°) Määritä tasojen MO 1 O suhteellinen sijainti

ja ADD 1, ABD 1 ja CO 1 C 1.

2°) Muodosta DCC 1 -tason ja suoran MO 1 leikkauspiste sekä MCC 1 ja A 1 D 1 C 1 -tasojen leikkauspiste.

3) Etsi kuution poikkileikkauspinta-ala tasosta, joka on yhdensuuntainen tason AD 1 C 1 kanssa ja kulkee pisteen O 1 kautta, jos kuution reuna on yhtä suuri kuin a.

208. Tetraedrin ABCD pisteet K, L, P ovat pintojen ABD, BDC, ABC massakeskuksia, vastaavasti, ja M on reunan AD keskipiste.

1°) Määritä ACD-tasojen suhteellinen sijainti

ja KLP; MLK ja ABC.

2°) Muodosta tason ABC ja suoran ML leikkauspiste sekä tasojen MKL ja ABC leikkauspiste.

3) Etsi tetraedrin poikkileikkauspinta-ala, joka kulkee pisteiden K, L ja M kautta yhdensuuntaisesti suoran AD kanssa, jos tetraedrin kaikki reunat ovat yhtä suuret kuin a.

209. Annettu kuutio ABCDA 1 B 1 C 1 D 1 . Pisteet L, M, M 1 ovat reunojen AB, AD ja A 1 D 1 keskipisteitä.

1°) Määritä tasojen B 1 D 1 D suhteellinen sijainti

ja LMM1.

2) Muodosta pisteen M kautta kulkeva taso, joka on yhdensuuntainen tason ACC 1 kanssa.

3) Muodosta kuution leikkaus, jonka taso kulkee pisteen M 1 kautta yhdensuuntaisesti tason CDD 1 kanssa.

4) Määritä tasojen MA 1 B 1 suhteellinen sijainti

ja CDM1.

5) Muodosta taso, joka kulkee linjan C 1 D 1 kautta yhdensuuntaisesti tason CDM 1 kanssa.

210. Oikealla tavalla nelikulmainen pyramidi SABCD:n kaikki reunat ovat yhtä suuret. Pisteet L, M ja N ovat reunojen AS, BS, CS keskipisteitä, vastaavasti.

1°) Määritä: suorien LM ja BC suhteellinen sijainti; suora LN ja taso ABD; lentokoneet LMN ja BDC.

2°) Osoita, että kolmiot ABC ja LMN ovat samanlaisia.

3) Rakenna pyramidin leikkaus käyttämällä tasoa AMN; kone LMN; kone LBC.

4*) Mikä pyramidin kärjen S läpi kulkevista osista on pinta-alaltaan suurin?

Viivojen ja tasojen rinnakkaisuus

SABC-tetraedrissä kaikki pinnat ovat säännöllisiä kolmioita. Pisteet L, M ja N ovat reunojen AS, BS, CS keskipisteitä, vastaavasti. 1°) Määritä suorien LM ja BC suhteellinen sijainti. 2°) Määritä suoran LN ja tason ABC suhteellinen sijainti.

3) Osoita, että kolmiot LMN ja ABC ovat samanlaisia.

Muodosta kuution leikkaus, joka on: 1°) tasasivuinen kolmio; 2) viisikulmio.

217. Muodosta tetraedrin osa, joka on suunnikas.

218°. Todista, että suuntaissärmiön vastakkaiset pinnat ovat yhdensuuntaiset.

219. Todista, että kaikkien läpi kulkevien suorien joukko tämä kohta ja yhdensuuntainen tietyn tason kanssa, muodostaa tason, joka on yhdensuuntainen annetun tason kanssa.

220. Annettu neljä pistettä A, B, C, D, jotka eivät ole samassa tasossa. Osoita, että jokainen suorien AB ja CD yhdensuuntainen taso leikkaa suorat AC, AD, BD, BC suunnikkaan pisteissä.

221. Osoita, että taso ja suora, joka ei kuulu tähän tasoon, ovat yhdensuuntaisia ​​toistensa kanssa, jos molemmat ovat samansuuntaisia ​​saman tason kanssa.

222. Kuution ABCDA 1 B 1 C 1 D 1 diagonaalien leikkauspisteen O kautta piirretään taso, joka on yhdensuuntainen pinnan ABCD kanssa. Tämä taso leikkaa reunat BB 1 ja CC 1 pisteissä M ja N. Todista, että kulma MON on suora kulma.

223. Todista, että kaksi tasoa ovat yhdensuuntaisia ​​toistensa kanssa, jos ja vain jos jokainen tasoista leikkaava suora leikkaa myös toisen.

224*. Kolmiopyramidissa SABC piirrä segmenttien AD ja CE kautta, missä D on SB:n keskipiste ja E on SA:n keskipiste, pyramidin leikkauksia toistensa kanssa yhdensuuntaisesti.

225. Etsi geometrisia paikkoja:

1) kaikkien segmenttien keskipisteet, joiden päät ovat kahdella tietyllä yhdensuuntaisella tasolla; 2*) janan keskipisteet, joiden päät ovat kahdella annetulla leikkaavalla suoralla.

226*. Tasossa α oleva kolmion ABC sivu AB on yhdensuuntainen tason β kanssa. Tasasivuinen kolmio A 1 B 1 C 1 on kolmion ABC yhdensuuntainen projektio tasolle β; AB = 5, BC = 6, AC = 9.

1) Määritä suorien AB ja A 1 B 1 suhteellinen sijainti,

BC ja B1 C1, A1 C1 ja AC.

2) Laske kolmion A 1 B 1 C 1 pinta-ala.

227*. Annettu kaksi leikkaavaa suoraa. Ilmoita kaikkien avaruuden pisteiden joukko, jonka läpi voidaan vetää viiva, joka leikkaa jokaisen kahdesta annetusta suorasta.

Perusmäärittely

Näitä kahta konetta kutsutaan

ovat yhdensuuntaisia,

jos niillä ei ole yhteisiä kohtia.

Tärkeimmät lausunnot

Rinnakkaismerkki - Jos tason yhden tason kaksi leikkaavaa suoraa ovat vastaavasti yhdensuuntaisia ​​toisen tason kahden suoran kanssa, niin nämä tasot

luut ovat yhdensuuntaiset.

Leikkauksen lause Jos kaksi yhdensuuntaista tasoa leikkaavat kaksi yhdensuuntaista tasoa ja leikkaavat kolmannen tason, niin tason kolmannen leikkauspisteen suorat

ne ovat yhdensuuntaisia.

a α,b α,a ×b ,c β, d β, a || c , b || d α || β

α || β, a = γ∩α, b = γ∩β a || b

Mα

β: α || p, Mp

Valmistautuminen teemaan

arviointiin aiheesta "Viivojen ja tasojen rinnakkaisuus"

Itsekontrollitehtävät

1. Nämä neljä pistettä eivät kuulu samaan tasoon. Voiko noin kolme heistä olla samalla suoralla?

2. Voiko kolmella eri tasolla olla täsmälleen kaksi yhteistä pistettä?

3. Voivatko kaksi vinoviivaa olla samansuuntaisia ​​kolmannen viivan kanssa samanaikaisesti?

4. Onko totta, että suoraan a ja b eivät ole yhdensuuntaisia, jos a:n ja b:n kanssa ei ole yhdensuuntaista suoraa c?

5. Voiko yhtä suurilla segmenteillä olla eriarvoisia projektioita?

6. Voiko säde olla suoran yhdensuuntainen projektio?

7. Voiko neliö olla kuution kuva?

8. Onko totta, että tietyn avaruuden pisteen kautta voidaan piirtää vain yksi taso yhdensuuntaisesti tietyn suoran kanssa?

9. Onko aina mahdollista piirtää viiva tietyn pisteen läpi yhdensuuntaisesti kahden tietyn tason kanssa, jotka eivät sisällä tätä pistettä?

10. Onko mahdollista piirtää yhdensuuntaisia ​​tasoja kahden leikkaavan suoran kautta?

Vastaukset itsehillintätehtäviin

Testinäyte

Kaksi suunnikasta ABCD ja ABC 1 D 1 ovat eri tasoissa.

1°) Määritä suorien CD ja C 1 D 1 suhteellinen sijainti.

2°) Määritä suoran C 1 D 1 ja tason suhteellinen sijainti

3°) Muodosta tasojen DD 1 C 1 ja ВСС 1 leikkausviiva.

4°) Määritä tasojen ADD 1 ja BCC 1 suhteellinen sijainti.

5) Piirrä pisteen M kautta jana AB suhteessa 2:1 pisteestä A laskettuna taso α, joka on yhdensuuntainen tason C 1 BC kanssa. 6) Muodosta suoran AC ja tason α leikkauspiste ja löydä suhde, jolla tämä piste jakaa janan AC.

Suorien viivojen ja tasojen suhteellinen sijainti avaruudessa

Trigonometrinen

Olet jo käsitellyt trigonometrisiä funktioita geometrian tunneilla. Tähän asti heidän sovelluksensa rajoittuivat pääasiassa kolmioiden ratkaisemiseen, eli puhuimme joidenkin kolmion elementtien löytämisestä toisista. Matematiikan historiasta tiedetään, että trigonometrian syntyminen liittyy pituuksien ja kulmien mittaamiseen. Nyt kuitenkin pallo

hänen sovellukset ovat paljon laajempia kuin muinaisina aikoina.

Sana "trigonometria" tulee kreikan sanasta τριγωνον

(trigonon) – kolmio ja µετρεω (metreo) – mitta, mitta-

minä haukkun. Kirjaimellisesti se tarkoittaa kolmioiden mittaamista.

SISÄÄN Tämä luku systematisoi geometriakurssilta jo tuntemasi materiaalin ja jatkaa opiskelua trigonometriset funktiot ja niiden sovellukset jaksollisten prosessien, erityisesti pyörimisliikkeen, värähtelyprosessien jne., karakterisointiin.

Useimmat trigonometrian sovellukset liittyvät erityisesti jaksollisiin prosesseihin, toisin sanoen prosesseihin, jotka toistuvat säännöllisin väliajoin. Auringonnousu ja auringonlasku, vuodenaikojen muutokset, pyörän pyöriminen - nämä ovat yksinkertaisimpia esimerkkejä tällaisista prosesseista. Mekaaniset ja sähkömagneettiset värähtelyt ovat myös tärkeitä esimerkkejä jaksollisista prosesseista. Siksi jaksollisten prosessien tutkiminen on tärkeä tehtävä. Ja matematiikan rooli sen ratkaisussa on ratkaiseva.

valmistaudutaan opiskelemaan aihetta "Trigonometriset funktiot"

Aiheen "Trigonometriset funktiot" tutkiminen kannattaa aloittaa tutustumalla kolmioiden kulmien trigonometristen funktioiden määritelmiin ja ominaisuuksiin sekä niiden sovelluksiin sekä suorakulmaisten että mielivaltaisten kolmioiden ratkaisemiseen.

Suorakulmaisten kulmien sini, kosini, tangentti, kotangentti

kolmio

Taulukko 24

Terävän kulman sini on vastakkaisen sivun suhde hypotenuusaan:

sin α = a c .

Terävän kulman kosini on viereisen jalan suhde hypotenuusaan:

cosα = b c .

Terävän kulman tangentti on vastakkaisen sivun suhde viereiseen sivuun:

tg α = a b .

Terävän kulman kotangentti on viereisen sivun suhde vastakkaiseen sivuun:

ctgα = a b .

Sini, kosini, tangentti, kulmien kotangentti 0° - 180°

Taulukko 25

sin α = Ry; cosa = Rx;

tg a = x y; pinnasänky α = x y.

(X; klo) - pisteen koordinaatit A sijaitsee ylemmässä puoliympyrässä, α - säteen muodostama kulma OA ympyrä akselilla X.

Sinin, kosinin, tangentin, kotangentin arvot

joitain kulmia

Taulukko 26

Kulma t

Mielivaltaisten kolmioiden ratkaiseminen

Taulukko 27

Sinien lause

Kolmion sivut ovat verrannollisia vastakkaisten kulmien sineihin:

synti aα = synti bβ = synti cγ .

Kosinilause

Kolmion mielivaltaisen sivun neliö on yhtä suuri kuin kahden muun sivun neliöiden summa ilman näiden sivujen tuloa niiden välisen kulman kosinilla:

c2 = a2 + b2 − 2 ab cos γ ,b2 = a2 + c2 − 2 ac cos β , a2 = b2 + c2 − 2 eKr cos α .

Kolmion pinta-ala on puolet sen kahden sivun tulosta ja niiden välisen kulman sinistä:

S= 1 2 absyntiγ = 1 2 acsyntiβ = 1 2 eKrsyntiα .

Trigonometriset perusidentiteetit

5. Vertaa mielivaltaisen suorakulmaisen kolmion terävien kulmien sinien summaa (merkitkää sitäA) yhden kanssa.

< 1. B.A= 1.

> 1. G. On mahdotonta verrata. Järjestä numerot nousevaan järjestykseen: A= sin 30°, b= cos 30°,

= tg 30°.

< b< c. B.a< c< b. SISÄÄN.c< a< b. G.b< a< c.

Vertaa teräviä kulmia α ja β ilman laskentatyökaluja, 7.

15. Määritä pisteen koordinaatitA, makaa ympyrällä, jonka säde on 1 (katso kuva).

(−1; 0). B.(1; 0).

(0; − 1). G.(0; 1).A.SISÄÄN.

Mikä tahansa tekninen toimenpide voidaan suorittaa tietyllä tarkkuudella, mikä tarkoittaa, että käsittelyn tuloksena saadun osan mitat eivät ole ihanteellisia, ne voivat vaihdella tietyllä alueella. Kokoamisehtojen täyttämiseksi ja osan luotettavan toiminnan varmistamiseksi tietyissä olosuhteissa on tarpeen asettaa hyväksyttävä aikaväli, jonka sisällä lopullisen koon tulee olla. Tämä intervalli voi säätää lineaaristen tai diametristen mittojen lisäksi myös pintojen muotoa tai suhteellista sijaintia.

Suunnittelija määrittää muodon ja sijainnin toleranssit asennusolosuhteiden ja mekanismin osan toiminta-ominaisuuksien perusteella.

Muototoleranssityypit

Muototoleranssi kutsutaan muotopoikkeaman suurimmaksi sallituksi arvoksi.

Muototoleranssikenttä- tämä on tasossa tai avaruudessa oleva alue, jonka sisällä tarkasteltavan elementin kaikkien pisteiden on sijaittava normalisoidulla alueella, jonka leveyden tai halkaisijan määrää toleranssiarvo, ja sijainti suhteessa todelliseen elementtiin viereisen elementin toimesta.

Muotopoikkeamat ja toleranssit

Seuraavat muotopoikkeamien toleranssit erotellaan:

• Poikkeama suoruudesta tasossa
• kupera
• koveruus
• Poikkeama tasosta ja tasaisuustoleranssi
• Kupera
• Koveruus
• Pyöreyden poikkeama ja pyöreyden toleranssi
• Ovaliteetti
• Leikata
• Sylinterimäisyyden poikkeama ja sylinterimäisyyden toleranssi
• Lieriömäisen pinnan pituusleikkausprofiilin poikkeama ja toleranssi
• Pitkittäisleikkausprofiilin poikkeama
• kartiomainen
• Tynnyri
• Satula

Sallitut poikkeamat on merkitty erityisillä symboleilla.

Sijaintitoleranssien tyypit

Sijaintitoleranssi- raja, joka rajoittaa sijaintipoikkeaman sallittua arvoa.

On olemassa sijaintitoleransseja ja suuntatoleransseja.

Sijainnin toleranssikenttä- tasossa tai avaruudessa oleva alue, jonka sisällä tulee olla viereinen elementti tai symmetriataso, akseli, keskipiste normalisoidun alueen sisällä, jonka halkaisija tai leveys määräytyy toleranssiarvon mukaan, ja sijainti suhteessa kyseisen elementin nimellispaikkaan.

Poikkeamat ja sijaintitoleranssit

Seuraavat sijaintitoleranssityypit erotellaan:

• Parallelismin poikkeama ja rinnakkaisuuden toleranssi
• Poikkeaman ja kohtisuoran toleranssi
• Poikkeama ja kaltevuustoleranssi
• Poikkeama- ja kohdistustoleranssi
• Toleranssi säteellä mitattuna
• Poikkeaman ja symmetrian toleranssi
• Paikkapoikkeama ja sijaintitoleranssi
• Toleranssi diametraalisesti
• Toleranssi säteellä mitattuna
• Leikkauspoikkeama ja akselin leikkaustoleranssi
• Toleranssi diametraalisesti
• Toleranssi säteellä mitattuna

Toleranssit yhteensä

Muodon ja sijainnin kokonaistoleransseja on useita.

• Radiaalinen juoksu
• Radial Runout yhteensä
• Aksiaalinen juoksu
• Täysi aksiaalinen juoksu
• Juoksu tiettyyn suuntaan
• Tietyn profiilin muodon poikkeama ja toleranssi
• Tietyn pinnan muodon poikkeama ja toleranssi

Nämä toleranssit on merkitty symboleilla.

Muoto- ja sijaintitoleranssien merkintä piirustuksissa

Muoto- ja sijaintitoleranssit on kuvattu piirustuksissa kehyksen muodossa, joka on jaettu useisiin osiin. Ensimmäinen osa kuvaa graafinen merkintä toleranssi, toisessa osassa - toleranssin numeerinen arvo, kolmannessa ja sitä seuraavissa osissa - yhden tai useamman emäksen kirjainmerkintä.

Jos toleranssipohjaa ei ole, runko koostuu vain kahdesta osasta. Kuvassa on esimerkkejä muodon ja sijainnin toleranssikehyksistä.

Vasemmalla olevassa kuvassa on kehys muototoleranssilla ( toleranssi suoruudesta), oikealla sijaintitoleranssilla (sallittu poikkeama yhdensuuntaisuudesta).

Kehys on tehty ohuilla linjoilla. Tekstin korkeuden kehyksessä tulee olla yhtä suuri kuin mittanumeroiden fonttikoko. Toleranssikehyksestä vedetään nuoleen päättyvä viiva pintaan tai johtoon.

Seuraavat merkit voidaan osoittaa ennen numeerista toleranssiarvoa:

• f - jos sylinterimäinen tai pyöreä toleranssikenttä ilmaistaan ​​halkaisijalla
• R - jos sylinterimäinen tai pyöreä kenttä on osoitettu säteellä
• T - jos akselien leikkauspisteen toleranssikenttä, symmetria, on rajoitettu kahteen samansuuntaiseen suoraan tai tasoon diametraalisesti.
• T/2 - samassa tapauksessa kuin T, vain säteen suhteen
• Pallo - pallomaiselle toleranssikentälle.

Jos toleranssia ei tule soveltaa koko pintaan, vaan vain tietylle alueelle, se osoitetaan katkoviivalla.

Yhdelle elementille voidaan määrittää useita toleransseja, jolloin kehykset näytetään päällekkäin.

lisäinformaatio voidaan osoittaa kehyksen ylä- tai alapuolelle.

Tiedot muodon ja sijainnin toleransseista voidaan määrittää.

Määrittämättömät kohdistustoleranssit standardin GOST 25069-81 mukaan.

Riippuvaiset toleranssit

Riippuvat sijainnin toleranssit on merkitty seuraavalla symbolilla.

Tämä symboli voidaan sijoittaa toleranssin numeroarvon jälkeen, jos riippuvainen toleranssi liittyy kyseisen elementin todellisiin mittoihin. Myös symboli voidaan sijoittaa kirjainmerkinnän jälkeen (jos se puuttuu, niin kehyksen kolmanteen kenttään), jos riippuvainen toleranssi liittyy peruselementin todellisiin mittoihin.

Muoto- ja sijaintitoleranssien määrittäminen

Mitä tarkemmin osa valmistetaan, sitä tarkempia työkaluja tarvitaan sen valmistukseen ja mittojen hallintaan. Tämä lisää automaattisesti sen kustannuksia. Osoittautuu, että osan valmistuskustannukset riippuvat suurelta osin vaaditusta tarkkuudesta sen valmistuksen aikana. Tämä tarkoittaa, että suunnittelijan tulee määrittää vain ne toleranssit, jotka ovat todella välttämättömiä mekanismin asennuksen ja luotettavan toiminnan kannalta. Hyväksyttävät aikavälit tulee myös määrittää keräys- ja suoritusolosuhteiden perusteella.

Numeeriset muototoleranssiarvot

Tarkkuusluokasta riippuen määritetään vakiomuototoleranssiarvot.

Tasaisuuden ja suoruuden toleranssit

Tässä tapauksessa nimelliskoon katsotaan olevan standardoidun osan nimellispituus.

Pyöreystoleranssit, sylinterimäisyys, pitkittäisprofiili

Nämä toleranssit määritetään tapauksissa, joissa niiden on oltava pienempiä kuin kokotoleranssi.

Nimelliskoko on nimellishalkaisija pinnat.

Toleranssit kohtisuorassa, yhdensuuntaisuudessa, kallistuksessa, aksiaalisuunnassa

Kun määritetään toleransseja yhdensuuntaisuudelle, kohtisuoralle ja kaltevuudelle, nimelliskoolla tarkoitetaan standardoidun osan nimelliskokoa tai koko säädellyn pinnan nimellispituutta.

Toleranssit säteittäiselle juoksulle, symmetrialle, akselien leikkauspisteen koaksiaalisuus diametraalisesti

Määritettäessä säteittäisen juoksutoleransseja nimelliskokona pidetään kyseisen pinnan nimellishalkaisijaa.

Kun määritetään symmetriatoleransseja, kohdistusakselin leikkauskohtaa, nimelliskokona pidetään pinnan nimellishalkaisijaa tai kyseisen elementin muodostavien pintojen välistä nimelliskokoa.

Jokainen, joka on koskaan opiskellut tai opiskelee koulussa, on joutunut kohtaamaan erilaisia ​​vaikeuksia opiskellessaan opetusministeriön kehittämään ohjelmaan sisältyviä tieteenaloja.

Mitä vaikeuksia kohtaat?

Kielten oppimiseen liittyy olemassa olevien kielioppisääntöjen ja niiden tärkeimpien poikkeuksien ulkoa opettelu. Liikunta vaatii opiskelijoilta paljon vaivaa, hyvä fyysinen kunto ja suurta kärsivällisyyttä.

Mikään ei kuitenkaan voi verrata tarkkoja tieteenaloja opiskellessa syntyviin vaikeuksiin. Algebra, joka sisältää monimutkaisia ​​tapoja ratkaista perustehtäviä. Fysiikka, jossa on runsaasti fysikaalisten lakien kaavoja. Geometria ja sen haarat, jotka perustuvat monimutkaisiin lauseisiin ja aksioomiin.

Esimerkkinä ovat rinnakkaisten tasojen teoriaa selittävät aksioomit, jotka on opetettava ulkoa, koska ne muodostavat koko kurssin perustan koulun opetussuunnitelma stereometrialla. Yritetään selvittää, kuinka tämä tehdään helpommin ja nopeammin.

Yhdensuuntaiset tasot esimerkein

Tasojen yhdensuuntaisuutta osoittava aksiooma on seuraava: " Mitä tahansa kahta tasoa pidetään yhdensuuntaisena vain, jos niillä ei ole yhteisiä pisteitä"eli ne eivät leikkaa toisiaan. Voit kuvitella tämän kuvan yksityiskohtaisemmin, kuten alkeellinen esimerkki Voit antaa katon ja lattian tai vastakkaisten seinien välisen suhteen rakennuksessa. Siitä tulee välittömästi selväksi, mitä tarkoitetaan, ja vahvistaa myös sen tosiasian, että nämä tasot normaalissa tapauksessa eivät koskaan leikkaa.

Toinen esimerkki olisi kaksinkertainen ikkuna, jossa lasilevyt toimivat tasoina. Ne eivät myöskään missään olosuhteissa muodosta risteyspisteitä keskenään. Tämän lisäksi voit lisätä kirjahyllyt, Rubikin kuutio, jossa tasot ovat sen vastakkaiset kasvot ja muut arkipäiväiset elementit.

Tarkasteltavat tasot on merkitty erityisellä merkillä kahden suoran viivan muodossa "||", jotka havainnollistavat selvästi tasojen yhdensuuntaisuutta. Siten käyttämällä todellisia esimerkkejä, voit muodostaa selkeämmän käsityksen aiheesta, ja siksi voit siirtyä tarkastelemaan monimutkaisempia käsitteitä.

Missä ja miten yhdensuuntaisten tasojen teoriaa sovelletaan?

Opiskellessaan koulun kurssi Geometriassa opiskelijat joutuvat käsittelemään erilaisia ​​ongelmia, joissa on usein tarpeen määrittää suorien, suorien ja tasojen yhdensuuntaisuus keskenään tai tasojen riippuvuus toisistaan. Analysoimalla olemassa olevaa tilaa jokainen tehtävä voidaan korreloida neljään stereometrian pääluokkaan.

Ensimmäinen luokka sisältää tehtävät, joissa on tarpeen määrittää suoran ja tason yhdensuuntaisuus toisiinsa nähden. Sen ratkaisu tulee samannimisen lauseen todistukseen. Tätä varten sinun on määritettävä, onko tarkasteltavana olevaan tasoon kuulumattomalla suoralla tässä tasossa yhdensuuntainen suora.

Toinen tehtäväluokka sisältää ne, joissa käytetään yhdensuuntaisten tasojen ominaisuutta. Sitä käytetään yksinkertaistamaan todistusprosessia, mikä lyhentää merkittävästi ratkaisun löytämiseen kuluvaa aikaa.

Seuraava luokka kattaa joukon ongelmia suorien viivojen vastaavuudesta tasojen yhdensuuntaisuuden perusominaisuuksiin. Ongelmanratkaisu neljäs luokka koostuu sen määrittämisestä, täyttyykö tasojen yhdensuuntaisuuden ehto. Kun tiedetään tarkalleen, kuinka tietyn ongelman todistelu tapahtuu, opiskelijoiden on helpompi navigoida, kun he käyttävät olemassa olevaa geometristen aksioomien arsenaalia.

Siten ongelmat, joiden ehdot edellyttävät suorien viivojen, suoran ja tason tai kahden keskenään välisen tason yhdensuuntaisuuden määrittämistä ja osoittamista. oikea valinta lause ja ratkaisu olemassa olevien sääntöjen mukaan.

Suoran ja tason yhdensuuntaisuudesta

Suoran ja tason samansuuntaisuus on stereometriassa erityinen aihe, koska se on juuri tätä peruskonsepti, johon kaikki seuraavat geometristen kuvioiden samansuuntaisuuden ominaisuudet perustuvat.

Käytettävissä olevien aksioomien mukaan siinä tapauksessa, että suoran kaksi pistettä kuuluvat tiettyyn tasoon, voimme päätellä, että myös tämä suora sijaitsee siinä. Tässä tilanteessa käy selväksi, että on olemassa kolme mahdollista vaihtoehtoa suoran sijainnille suhteessa tasoon avaruudessa:

1. Suora kuuluu tasoon.
2. Suoralla ja tasolla on yksi yhteinen leikkauspiste.
3. Suoralle ja tasolle ei ole leikkauspisteitä.

Olemme erityisesti kiinnostuneita viimeisestä vaihtoehdosta, kun risteyspisteitä ei ole. Vasta sitten voidaan sanoa, että suora ja taso ovat yhdensuuntaiset toisiinsa nähden. Siten vahvistetaan päälauseen ehto suoran ja tason yhdensuuntaisuuden merkistä, joka sanoo, että: "Jos suora, joka ei kuulu tarkasteltavana olevaan tasoon, on yhdensuuntainen minkä tahansa tämän tason suoran kanssa, on tarkasteltava suora myös yhdensuuntainen annetun tason kanssa."

Tarve käyttää rinnakkaisuusominaisuutta

Tasojen yhdensuuntaisuuden merkkiä käytetään yleensä yksinkertaistetun ratkaisun löytämiseen tasoihin liittyviin ongelmiin. Tämän ominaisuuden olemus on seuraava: " Jos on kaksi leikkaavaa suoraa, jotka ovat samassa tasossa, yhdensuuntaisia ​​kahden toiseen tasoon kuuluvan suoran kanssa, niin tällaisia ​​tasoja voidaan kutsua yhdensuuntaisiksi.».

Lisälauseita

Tasojen yhdensuuntaisuuden osoittavan merkin käytön lisäksi käytännössä voidaan kohdata kahden muun lisälauseen käyttö. Ensimmäinen esitetään seuraavassa muodossa: " Jos toinen kahdesta yhdensuuntaisesta tasosta on yhdensuuntainen kolmannen kanssa, toinen taso on joko yhdensuuntainen kolmannen kanssa tai on täysin yhdensuuntainen sen kanssa».

Annettujen lauseiden käytön perusteella on aina mahdollista todistaa tasojen yhdensuuntaisuus tarkasteltavana olevan avaruuden suhteen. Toinen lause näyttää tasojen riippuvuuden kohtisuorasta suorasta ja sen muoto on: " Jos kaksi erilaista tasoa ovat kohtisuorassa tiettyä suoraa vastaan, ne katsotaan yhdensuuntaisiksi toistensa kanssa».

Välttämättömien ja riittävien ehtojen käsite

Ratkaisemalla toistuvasti tasojen yhdensuuntaisuuden todistustehtäviä johdettiin välttämätön ja riittävä ehto tasojen yhdensuuntaisuudelle. Tiedetään, että mikä tahansa taso on annettu parametrisella yhtälöllä muotoa: A 1 x+ B 1 y+ C 1 z+D 1 =0. Ehdomme perustuu yhtälöjärjestelmän käyttöön, joka määrittää tasojen sijainnin avaruudessa, ja sitä edustaa seuraava muotoilu: " Kahden tason yhdensuuntaisuuden todistamiseksi on välttämätöntä ja riittävää, että näitä tasoja kuvaava yhtälöjärjestelmä on epäjohdonmukainen, eli sillä ei ole ratkaisua».

Perusominaisuudet

Geometristen tehtävien ratkaisussa rinnakkaisuusominaisuuden käyttö ei kuitenkaan aina riitä. Joskus syntyy tilanne, kun on tarpeen todistaa kahden tai useamman suoran samansuuntaisuus eri tasoissa tai näiden suorien sisältämien segmenttien yhtäläisyys. Käytä tätä varten tasojen yhdensuuntaisuuden ominaisuuksia. Geometriassa niitä on vain kaksi.

Ensimmäinen ominaisuus antaa meille mahdollisuuden arvioida suorien yhdensuuntaisuutta tietyissä tasoissa ja se esitetään seuraavassa muodossa: " Jos kaksi yhdensuuntaista tasoa leikkaa kolmannen, niin leikkausviivojen muodostamat suorat ovat myös yhdensuuntaisia ​​toistensa kanssa».

Toisen ominaisuuden tarkoitus on todistaa rinnakkaisilla viivoilla sijaitsevien segmenttien yhtäläisyys. Sen tulkinta on esitetty alla. " Jos tarkastelemme kahta yhdensuuntaista tasoa ja suljemme alueen niiden väliin, voimme sanoa, että tämän alueen muodostamien segmenttien pituus on sama».