Jednadžba kosinusa x jednaka je a. Trigonometrijske jednadžbe - formule, rješenja, primjeri. Faktorizacija
Možete naručiti detaljno rješenje vašeg problema !!!
Jednakost koja sadrži nepoznanicu pod znakom trigonometrijske funkcije (`sin x, cos x, tan x` ili` ctg x`) naziva se trigonometrijska jednadžba, a njihove formule ćemo dalje razmatrati.
Najjednostavnije jednadžbe nazivaju se `sin x = a, cos x = a, tg x = a, ctg x = a`, gdje je `x` kut koji treba pronaći, `a` je bilo koji broj. Zapišimo formule korijena za svaku od njih.
1. Jednadžba `sin x = a`.
Za `| a |> 1` nema rješenja.
Za `| a | \ leq 1` ima beskonačan broj rješenja.
Formula korijena: `x = (- 1) ^ n arcsin a + \ pi n, n \ in Z`
2. Jednadžba `cos x = a`
Za `| a |> 1` - kao u slučaju sinusa, nema rješenja među realnim brojevima.
Za `| a | \ leq 1` ima beskonačan broj rješenja.
Formula korijena: `x = \ pm arccos a + 2 \ pi n, n \ in Z`
Posebni slučajevi za sinus i kosinus u grafovima. 
3. Jednadžba `tg x = a`
Ima beskonačan broj rješenja za bilo koju vrijednost `a`.
Formula korijena: `x = arctan a + \ pi n, n \ in Z`
4. Jednadžba `ctg x = a`
Također ima beskonačan broj rješenja za bilo koje vrijednosti `a`.
Formula korijena: `x = arcctg a + \ pi n, n \ in Z`
Formule za korijene trigonometrijskih jednadžbi u tablici
za sinus: 
za kosinus: 
Za tangentu i kotangens: 
Formule za rješavanje jednadžbi koje sadrže inverzne trigonometrijske funkcije:
Metode rješavanja trigonometrijskih jednadžbi
Rješenje bilo koje trigonometrijske jednadžbe sastoji se od dvije faze:
- pomoću pretvoriti ga u najjednostavniji;
- riješite rezultirajuću najjednostavniju jednadžbu koristeći gore napisane korijenske formule i tablice.
Pogledajmo primjere glavnih metoda rješavanja.
Algebarska metoda.
U ovoj metodi vrši se zamjena varijable i zamjena u jednakost.
Primjer. Riješite jednadžbu: `2cos ^ 2 (x + \ frac \ pi 6) -3sin (\ frac \ pi 3 - x) + 1 = 0`
`2cos ^ 2 (x + \ frac \ pi 6) -3cos (x + \ frac \ pi 6) + 1 = 0`,
vršimo promjenu: `cos (x + \ frac \ pi 6) = y`, zatim` 2y ^ 2-3y + 1 = 0`,
nalazimo korijene: `y_1 = 1, y_2 = 1 / 2`, odakle slijede dva slučaja:
1.` cos (x + \ frac \ pi 6) = 1`, `x + \ frac \ pi 6 = 2 \ pi n`,` x_1 = - \ frac \ pi 6 + 2 \ pi n`.
2.` cos (x + \ frac \ pi 6) = 1 / 2`, `x + \ frac \ pi 6 = \ pm arccos 1/2 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`.
Odgovor: `x_1 = - \ frac \ pi 6 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`.
Faktorizacija.
Primjer. Riješite jednadžbu: `sin x + cos x = 1`.
Riješenje. Pomaknite sve članove jednakosti ulijevo: `sin x + cos x-1 = 0`. Korištenje, transformacija i faktoriranje lijeve strane:
`grijeh x - 2sin ^ 2 x / 2 = 0`,
`2sin x / 2 cos x / 2-2sin ^ 2 x / 2 = 0`,
`2sin x / 2 (cos x / 2-sin x / 2) = 0`,
- `grijeh x / 2 = 0`,` x / 2 = \ pi n`, `x_1 = 2 \ pi n`.
- `cos x / 2-sin x / 2 = 0`,` tg x / 2 = 1`, `x / 2 = arktan 1+ \ pi n`,` x / 2 = \ pi / 4 + \ pi n` , `x_2 = \ pi / 2 + 2 \ pi n`.
Odgovor: `x_1 = 2 \ pi n`,` x_2 = \ pi / 2 + 2 \ pi n`.
Redukcija na homogenu jednadžbu
Prvo, morate ovu trigonometrijsku jednadžbu dovesti na jednu od dvije vrste:
`a sin x + b cos x = 0` (homogena jednadžba prvog stupnja) ili` a sin ^ 2 x + b sin x cos x + c cos ^ 2 x = 0` (homogena jednadžba drugog stupnja).
Zatim podijelite oba dijela sa `cos x \ ne 0` - za prvi slučaj, i s` cos ^ 2 x \ ne 0` - za drugi. Dobivamo jednadžbe za `tg x`:` a tg x + b = 0` i `a tg ^ 2 x + b tg x + c = 0`, koje je potrebno riješiti poznatim metodama.
Primjer. Riješite jednadžbu: `2 sin ^ 2 x + sin x cos x - cos ^ 2 x = 1`.
Riješenje. Prepišite desnu stranu kao `1 = sin ^ 2 x + cos ^ 2 x`:
`2 sin ^ 2 x + sin x cos x - cos ^ 2 x =` `sin ^ 2 x + cos ^ 2 x`,
`2 sin ^ 2 x + sin x cos x - cos ^ 2 x -` `sin ^ 2 x - cos ^ 2 x = 0`
`grijeh ^ 2 x + sin x cos x - 2 cos ^ 2 x = 0`.
Ovo je homogena trigonometrijska jednadžba drugog stupnja, njezinu lijevu i desnu stranu podijelimo s `cos ^ 2 x \ ne 0`, dobivamo:
`\ frac (sin ^ 2 x) (cos ^ 2 x) + \ frac (sin x cos x) (cos ^ 2 x) - \ frac (2 cos ^ 2 x) (cos ^ 2 x) = 0`
`tg ^ 2 x + tg x - 2 = 0`. Uvodimo zamjenu `tg x = t`, kao rezultat,` t ^ 2 + t - 2 = 0`. Korijeni ove jednadžbe su `t_1 = -2` i` t_2 = 1`. Zatim:
- `tg x = -2`,` x_1 = arctg (-2) + \ pi n`, `n \ u Z`
- `tg x = 1`,` x = arktan 1+ \ pi n`, `x_2 = \ pi / 4 + \ pi n`,` n \ u Z`.
Odgovor. `x_1 = arctg (-2) + \ pi n`,` n \ u Z`, `x_2 = \ pi / 4 + \ pi n`,` n \ u Z`.
Idi do pola kuta
Primjer. Riješite jednadžbu: `11 sin x - 2 cos x = 10`.
Riješenje. Primijenite formule dvostrukog kuta, kao rezultat: `22 sin (x / 2) cos (x / 2) -`` 2 cos ^ 2 x / 2 + 2 sin ^ 2 x / 2 =` `10 sin ^ 2 x / 2 +10 cos ^ 2 x / 2`
`4 tg ^ 2 x / 2 - 11 tg x / 2 + 6 = 0`
Primjenom gornje algebarske metode dobivamo:
- `tg x / 2 = 2`,` x_1 = 2 arktan 2 + 2 \ pi n`, `n \ u Z`,
- `tg x / 2 = 3 / 4`,` x_2 = arktan 3/4 + 2 \ pi n`, `n \ u Z`.
Odgovor. `x_1 = 2 arktan 2 + 2 \ pi n, n \ u Z`,` x_2 = arktan 3/4 + 2 \ pi n`, `n \ u Z`.
Uvesti pomoćni kut
U trigonometrijskoj jednadžbi `a sin x + b cos x = c`, gdje su a, b, c koeficijenti, a x je varijabla, obje strane dijelimo sa` sqrt (a ^ 2 + b ^ 2) `:
`\ frac a (sqrt (a ^ 2 + b ^ 2)) sin x +` `\ frac b (sqrt (a ^ 2 + b ^ 2)) cos x = '' \ frac c (sqrt (a ^ 2) + b ^ 2)) `.
Koeficijenti na lijevoj strani imaju svojstva sinusa i kosinusa, naime, zbroj njihovih kvadrata je jednak 1 i njihove apsolutne vrijednosti nisu veće od 1. Označavamo ih na sljedeći način: `\ frac a (sqrt ( a ^ 2 + b ^ 2)) = cos \ varphi` , `\ frac b (sqrt (a ^ 2 + b ^ 2)) = sin \ varphi`,` \ frac c (sqrt (a ^ 2 + b ^ 2)) = C`, tada:
`cos \ varphi sin x + sin \ varphi cos x = C`.
Pogledajmo pobliže sljedeći primjer:
Primjer. Riješite jednadžbu: `3 sin x + 4 cos x = 2`.
Riješenje. Podijelimo obje strane jednakosti sa `sqrt (3 ^ 2 + 4 ^ 2)`, dobivamo:
`\ frac (3 sin x) (sqrt (3 ^ 2 + 4 ^ 2)) +` `\ frac (4 cos x) (sqrt (3 ^ 2 + 4 ^ 2)) = '' \ frac 2 (sqrt (3 ^ 2 + 4 ^ 2)) `
`3/5 sin x + 4/5 cos x = 2 / 5`.
Označimo `3/5 = cos \ varphi`,` 4/5 = sin \ varphi`. Budući da je `sin \ varphi> 0`,` cos \ varphi> 0`, tada uzimamo `\ varphi = arcsin 4 / 5` kao pomoćni kut. Tada našu jednakost zapisujemo u obliku:
`cos \ varphi sin x + sin \ varphi cos x = 2 / 5`
Primjenjujući formulu za zbroj kutova za sinus, zapisujemo našu jednakost u sljedećem obliku:
`grijeh (x + \ varphi) = 2 / 5`,
`x + \ varphi = (- 1) ^ n arcsin 2/5 + \ pi n`,` n \ u Z`,
`x = (- 1) ^ n arcsin 2/5-` `arcsin 4/5 + \ pi n`,` n \ u Z`.
Odgovor. `x = (- 1) ^ n arcsin 2/5-` `arcsin 4/5 + \ pi n`,` n \ u Z`.
Frakcijsko-racionalne trigonometrijske jednadžbe
To su jednakosti s razlomcima s trigonometrijskim funkcijama u brojnicima i nazivnicima.
Primjer. Riješite jednadžbu. `\ frac (sin x) (1 + cos x) = 1-cos x`.
Riješenje. Pomnožite i podijelite desnu stranu jednakosti s `(1 + cos x)`. Kao rezultat, dobivamo:
`\ frac (sin x) (1 + cos x) = '' \ frac ((1-cos x) (1 + cos x)) (1 + cos x)`
`\ frac (sin x) (1 + cos x) =` `\ frac (1-cos ^ 2 x) (1 + cos x)`
`\ frac (sin x) (1 + cos x) =` `\ frac (sin ^ 2 x) (1 + cos x)`
`\ frac (sin x) (1 + cos x) -`` \ frac (sin ^ 2 x) (1 + cos x) = 0`
`\ frac (sin x-sin ^ 2 x) (1 + cos x) = 0`
S obzirom da nazivnik ne može biti jednak nuli, dobivamo `1 + cos x \ ne 0`,` cos x \ ne -1`, `x \ ne \ pi + 2 \ pi n, n \ u Z`.
Izjednačite brojnik razlomka s nulom: `sin x-sin ^ 2 x = 0`,` sin x (1-sin x) = 0`. Tada je `sin x = 0` ili` 1-sin x = 0`.
- `sin x = 0`,` x = \ pi n`, `n \ in Z`
- `1-sin x = 0`,` sin x = -1`, `x = \ pi / 2 + 2 \ pi n, n \ u Z`.
S obzirom da je `x \ ne \ pi + 2 \ pi n, n \ u Z`, rješenja su ` x = 2 \ pi n, n \ u Z` i `x = \ pi / 2 + 2 \ pi n` , `n \ u Z`.
Odgovor. `x = 2 \ pi n`,` n \ u Z`, `x = \ pi / 2 + 2 \ pi n`,` n \ u Z`.
Trigonometrija, a posebno trigonometrijske jednadžbe, koriste se u gotovo svim područjima geometrije, fizike, inženjerstva. Učenje počinje u 10. razredu, sigurno ima zadataka za ispit, pa pokušajte zapamtiti sve formule trigonometrijskih jednadžbi - one će vam svakako dobro doći!
Međutim, ne trebate ih čak ni pamtiti, glavno je razumjeti suštinu i moći ih zaključiti. Nije tako teško kao što zvuči. Uvjerite se sami gledajući video.
Najjednostavnije trigonometrijske jednadžbe obično se rješavaju formulama. Dopustite mi da vas podsjetim da se sljedeće trigonometrijske jednadžbe nazivaju najjednostavnijim:
sinx = a
cosx = a
tgx = a
ctgx = a
x je kut koji treba pronaći,
a - bilo koji broj.
A evo i formula s kojima možete odmah zapisati rješenja ovih najjednostavnijih jednadžbi.
za sinus:
za kosinus:
h = ± arccos a + 2π n, n ∈ Z
za tangentu:
x = arctan a + π n, n ∈ Z
za kotangens:
x = arcctg a + π n, n ∈ Z
Zapravo, ovo je teorijski dio rješavanja najjednostavnijih trigonometrijskih jednadžbi. Štoviše, sve!) Baš ništa. Međutim, broj pogrešaka na ovoj temi jednostavno je izvan skale. Pogotovo ako primjer malo odstupa od predloška. Zašto?
Da, jer mnogi ljudi zapisuju ova slova, uopće ne shvaćajući njihovo značenje! Oprezno zapisuje, bez obzira na to kako se nešto dogodilo ...) S tim se mora riješiti. Trigonometrija za ljude, ili ljudi za trigonometriju ipak!?)
Hoćemo li to shvatiti?
Jedan kut bit će jednak arccos a, drugi: -arccos a.
I uvijek će tako funkcionirati. Za bilo koje a.
Ako mi ne vjerujete, zadržite pokazivač miša iznad slike ili dodirnite sliku na tabletu.) Promijenio sam broj a na neke negativne. U svakom slučaju, imamo jedan kut arccos a, drugi: -arccos a.
Stoga se odgovor uvijek može napisati u obliku dva niza korijena:
x 1 = arccos a + 2π n, n ∈ Z
x 2 = - arccos a + 2π n, n ∈ Z
Kombiniramo ove dvije serije u jednu:
x = ± arccos a + 2π n, n ∈ Z
I to je sve. Dobili smo opću formulu za rješavanje najjednostavnije trigonometrijske jednadžbe s kosinusom.
Ako shvatite da to nije neka superznanstvena mudrost, ali samo skraćena oznaka dvije serije odgovora, ti i zadatak "C" bit ćeš na ramenu. S nejednakostima, s odabirom korijena iz zadanog intervala... Tamo odgovor s plus/minus ne valja. A ako se prema odgovoru odnosite na poslovni način i podijelite ga na dva odvojena odgovora, sve je odlučeno.) Zapravo, za to razumijemo. Što, kako i gdje.
U najjednostavnijoj trigonometrijskoj jednadžbi
sinx = a
također se dobivaju dvije serije korijena. Je uvijek. A mogu se i ove dvije serije snimiti jedna linija. Samo će ova linija biti lukavija:
h = (-1) n arcsin a + π n, n ∈ Z
Ali suština ostaje ista. Matematičari su jednostavno konstruirali formulu kako bi napravili jedan umjesto dva zapisa niza korijena. I to je to!
Provjerimo matematičare? A onda se nikad ne zna...)
U prethodnoj lekciji detaljno je analizirano rješenje (bez ikakvih formula) trigonometrijske jednadžbe sa sinusom:
Odgovor je proizveo dvije serije korijena:
x 1 = π / 6 + 2π n, n ∈ Z
x 2 = 5π / 6 + 2π n, n ∈ Z
Ako istu jednadžbu riješimo pomoću formule, dobivamo odgovor:
x = (-1) n arcsin 0,5 + π n, n ∈ Z
Zapravo, ovo je nedovršen odgovor.) Učenik to mora znati arcsin 0,5 = π / 6. Potpuni odgovor bi bio:
x = (-1) n π / 6+ π n, n ∈ Z
Ovo postavlja zanimljivo pitanje. Odgovorite putem x 1; x 2 (to je pravi odgovor!) i kroz usamljene NS (a ovo je točan odgovor!) - ista stvar, ili ne? Sad ćemo saznati.)
Zamjena kao odgovor sa x 1 značenje n = 0; 1; 2; i tako dalje, računamo, dobivamo niz korijena:
x 1 = π / 6; 13π / 6; 25π / 6 itd.
Uz istu zamjenu u odgovoru sa x 2 , dobivamo:
x 2 = 5π / 6; 17π / 6; 29π / 6 itd.
Sada zamjenjujemo vrijednosti n (0; 1; 2; 3; 4 ...) u opću formulu za usamljenog NS ... Odnosno, podižemo minus jedan na nulu, zatim na prvi, drugi itd. I, naravno, zamjenjujemo 0 u drugom članu; 1; 2 3; 4 itd. I računamo. Dobijamo seriju:
x = π / 6; 5π / 6; 13π / 6; 17π / 6; 25π / 6 itd.
To je sve što možete vidjeti.) Opća formula nam daje potpuno isti rezultati, kao dva odgovora odvojeno. Samo odjednom, redom. Neka vas matematičari ne zavaraju.)
Također se mogu provjeriti formule za rješavanje trigonometrijskih jednadžbi s tangentom i kotangensom. Ali nećemo.) Tako su jednostavni.
Namjerno sam opisao svu tu zamjenu i provjeru. Ovdje je važno razumjeti jednu jednostavnu stvar: postoje formule za rješavanje elementarnih trigonometrijskih jednadžbi, samo kratak zapis odgovora. Za ovu kratkoću, morao sam ubaciti plus/minus u kosinusnu otopinu i (-1) n u otopinu sinusa.
Ovi umetci ni na koji način ne ometaju zadatke u kojima samo trebate zapisati odgovor na elementarnu jednadžbu. Ali ako trebate riješiti nejednakost, ili onda trebate učiniti nešto s odgovorom: odabrati korijene na intervalu, provjeriti ODZ itd., ovi umetci mogu lako uznemiriti osobu.
I što učiniti? Da, ili zapišite odgovor u dva niza, ili riješite jednadžbu/nejednadžbu duž trigonometrijskog kruga. Tada ti umetci nestaju i život postaje lakši.)
Možemo rezimirati.
Postoje gotove formule odgovora za rješavanje najjednostavnijih trigonometrijskih jednadžbi. Četiri komada. Dobre su za trenutno snimanje rješenja jednadžbe. Na primjer, trebate riješiti jednadžbe:
sinx = 0,3
Lako: h = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Nema problema: h = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Lako: x = arktan 1,2 + π n, n ∈ Z
ctgx = 3,7
jedan ostao: x = arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Ako ti, blistajući znanjem, odmah napišeš odgovor:
x = ± arccos 1,8 + 2π n, n ∈ Z
onda već sjajiš, ovo ... ono ... iz lokve.) Točan odgovor: nema rješenja. Shvaćate li zašto? Pročitajte što je arkosinus. Osim toga, ako su tablične vrijednosti sinusa, kosinusa, tangenta, kotangensa na desnoj strani izvorne jednadžbe, - 1; 0; √3; 1/2; √3/2 itd. - odgovor će kroz lukove biti nedovršen. Lukovi se moraju prevesti u radijane.
A ako naiđete na nejednakost poput
onda je odgovor:
h πn, n ∈ Z
postoji rijetka glupost, da ...) Ovdje je potrebno odlučiti se za trigonometrijski krug. Što ćemo učiniti u relevantnoj temi.
Za one koji su herojski pročitali ove redove. Jednostavno ne mogu ne cijeniti tvoje titanske napore. Ti si bonus.)
Bonus:
Kada pišu formule u alarmantnom borbenom okruženju, čak se i akademski okorjeli štreberi često zbune oko toga gdje πn, I gdje 2π n. Evo jednostavnog trika. U od svega formule vrijedne πn. Osim jedine formule s inverznim kosinusom. Tu stoji 2πn. Dva pien. Ključna riječ - dva. Ista formula sadrži dva znak na početku. Plus i minus. Tu i tamo - dva.
Pa ako ste napisali dva znak ispred inverznog kosinusa, lakše je zapamtiti što će biti na kraju dva pien. Pa čak se događa i suprotno. Preskoči muški znak ± , dolazi do kraja, piše kako treba dva pien, i doći će k sebi. Ispred nečega dva znak! Osoba će se vratiti na početak, ali će ispraviti grešku! Kao ovo.)
Ako vam se sviđa ova stranica...
Usput, imam još nekoliko zanimljivih stranica za vas.)
Možete vježbati rješavanje primjera i saznati svoju razinu. Trenutno testiranje valjanosti. Učenje - sa zanimanjem!)
možete se upoznati s funkcijama i izvedenicama.
Zakharova Ljudmila Vladimirovna
MBOU "Srednja škola br. 59" u Barnaulu
nastavnik matematike
[e-mail zaštićen]
№1 Najjednostavnije trigonometrijske jednadžbe
Cilj: 1. Izvedi formule za rješenja najjednostavnijih trigonometrijskih jednadžbi oblika sinx = a, cosx = a, tgx = a, ctgx = a;
2. Naučite rješavati najjednostavnije trigonometrijske jednadžbe pomoću formula.
Oprema: 1) Tablice s grafovima trigonometrijskih funkcija y = sinx, y = cosx, y = tgx, y = ctgx; 2) Tablica vrijednosti inverznih trigonometrijskih funkcija; 3) Zbirna tablica formula za rješavanje najjednostavnijih trigonometrijskih jednadžbi.
Plan predavanja:
1 Izvođenje formula za korijene jednadžbe
a) sinx = a,
b) cosx = a,
c) tgx = a,
d) ctgx = a.
2 ... Usmeni frontalni rad za konsolidaciju dobivenih formula.
3 ... Pisani rad za konsolidaciju proučenog gradiva
Tijekom nastave.U algebri, geometriji, fizici i drugim predmetima susrećemo se s raznim problemima čije je rješenje povezano s rješavanjem jednadžbi. Proučavali smo svojstva trigonometrijskih funkcija pa je prirodno prijeći na jednadžbe u kojima je nepoznata sadržana pod znakom funkcija
Definicija: Jednadžbe oblika sinx = a , cosx= a , tgx= a , ctgx= a nazivaju se najjednostavnijim trigonometrijskim jednadžbama.
Vrlo je važno naučiti rješavati najjednostavnije trigonometrijske jednadžbe, budući da se sve metode i tehnike rješavanja bilo koje trigonometrijske jednadžbe svode na one najjednostavnije.
Počnimo s izvođenjem formula koje "aktivno" rade pri rješavanju trigonometrijskih jednadžbi.
1.Jednadžbe oblika sinx = a.
Riješimo jednadžbu sinx = a grafički. Da bismo to učinili, u jednom koordinatnom sustavu crtamo grafove funkcija y = sinx i y = a.
1) Ako a> 1 i a grijeh x = a nema rješenja, budući da pravac i sinusoida nemaju zajedničkih točaka.
2) Ako -1a a prelazi sinusoidu beskonačno mnogo puta. To znači da je jednadžba sinx = a ima beskonačno mnogo rješenja.
Budući da je period sinusa 2 
, zatim za rješavanje jednadžbe sinx = a dovoljno je pronaći sva rješenja na bilo kojem segmentu duljine 2.
Rješavanjem jednadžbe za [- / 2; / 2] po definiciji arcsinusa x = arcsin a, a na x = -arcsin a... Uzimajući u obzir periodičnost funkcije y = sinx, dobivamo sljedeće izraze
x = -arcsin a+ 2n, n Z.
Obje serije rješenja mogu se kombinirati
X = (-1) n arcsin a+ n, nZ.
U sljedeća tri slučaja radije koriste ne opću formulu, već jednostavnije odnose:
Ako a= -1, tada sin x = -1, x = - / 2 + 2n
Ako a= 1, tada je sin x = 1, x = / 2 + 2n
Ako a = 0, tada je sin x = 0. x = n,
Primjer: Riješite jednadžbu sinx = 1/2.
Sastavimo formule za rješenja x = arcsin 1/2 + 2n
X = - arcsin a + 2n
Izračunajmo vrijednost arcsin1/2. Zamijenite pronađenu vrijednost u formule rješenja
x = 5/6 + 2 n
ili općom formulom
X = (-1) n arcsin 1/2 + n,
X = (-1) n / 6 + n,
2. Jednadžbe oblika cosx = a.
Riješimo jednadžbu cosx = a također grafički, crtanje grafova funkcija y = cosx i y = a.
1) Ako je a 1, onda jednadžba cosx = a nema rješenja, budući da grafovi nemaju zajedničkih točaka.
2) Ako je -1 a cosx = a ima beskonačan broj rješenja.
Naći ćemo sva rješenja cosx = a na intervalu duljine 2 jer je period kosinusa 2.
Na rješenju jednadžbe po definiciji arkosinusa bit će x = arcos a. S obzirom na paritet kosinusne funkcije, rješenje jednadžbe na [-; 0] bit će x = -arcos a.
Dakle, rješenja jednadžbe cosx = a x = + arcos a+ 2 n,
U tri slučaja koristit ćemo ne opću formulu, već jednostavnije relacije:
Ako a= -1, tada je cosx = -1, x = - / 2 + 2n
Ako a= 1, tada je cosx = 1, x = 2n,
Ako je a = 0, tada je cosx = 0. x = / 2 + n
Primjer: Riješite jednadžbu cos x = 1/2,
Sastavimo formule za rješenja x = arccos 1/2 + 2n
Izračunajmo vrijednost arccos1 / 2.
Zamijenite pronađenu vrijednost u formule rješenja
X = + /3+ 2n, nZ.
Jednadžbe oblika tgx = a.
Kako je period tangente jednak, onda da bi se pronašla sva rješenja jednadžbe tgx = a, dovoljno je pronaći sva rješenja na bilo kojem intervalu duljine. Prema definiciji arktangenta, rješenje jednadžbe na (- / 2; / 2) je arktan a. Uzimajući u obzir period funkcije, sva rješenja jednadžbe mogu se zapisati u obliku
x = arctg a+ n, nZ.
Primjer: Riješite jednadžbu tg x = 3/3
Sastavimo formulu za rješavanje x = arktan 3/3 + n, nZ.
Izračunavamo vrijednost arktangensa arktan 3/3 = / 6, dakle
X = / 6 + n, nZ.
Izvođenje formule za rješavanje jednadžbe s tgx= a može se pružiti studentima.
Primjer.
Riješite jednadžbu ctg x = 1.
x = arcctg 1 + n, nZ,
X = / 4 + n, nZ.
Kao rezultat proučenog materijala, učenici mogu ispuniti tablicu:
"Rješavanje trigonometrijskih jednadžbi."
jednadžba
Vježbe za učvršćivanje proučenog gradiva.
(Usmeno) Koja se od zapisanih jednadžbi može riješiti formulama:
a) x = (-1) n arcsin a+ n, nZ;
b) x = + arcos a + 2 n?
cos x = 2/2, tg x = 1, sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 ...
Koja od navedenih jednadžbi nema rješenja?
Riješite jednadžbe:
a) sin x = 0; e) sin x = 2/2; h) sin x = 2;
b) cos x = 2/2; f) cos x = -1/2; i) cos x = 1;
d) tg x = 3; g) ctg x = -1; j) tg x = 1/3.
3. Riješite jednadžbe:
a) sin 3x = 0; e) 2cos x = 1;
b) cos x / 2 = 1/2; f) 3 tan 3x = 1;
d) sin x / 4 = 1; g) 2cos (2x + / 5) = 3.
Prilikom rješavanja ovih jednadžbi korisno je zapisati pravila za rješavanje jednadžbi oblika grijeh v x = a, i s grijeh v x = a, | a|1.
Grijeh v x = a, | a | 1.
v x = (-1) n arcsin a+ n, nZ,
x = (-1) n 1 / v arcsin a+ n / v, nZ.
Sumiranje rezultata lekcije:
Danas smo na satu izveli formule za rješavanje najjednostavnijih trigonometrijskih jednadžbi.
Rastavljeni primjeri rješavanja najjednostavnijih trigonometrijskih jednadžbi.
Ispunili smo tablicu koju ćemo koristiti za rješavanje jednadžbi.
Domaća zadaća.
№2 Rješavanje trigonometrijskih jednadžbi
Cilj: Proučiti metode rješavanja trigonometrijskih jednadžbi: 1) svodive na kvadratne, 2) svodive na homogene trigonometrijske jednadžbe.
Razvijati sposobnosti zapažanja učenika pri korištenju različitih metoda rješavanja trigonometrijskih jednadžbi.
Frontalni rad s učenicima.
Koje su formule za korijene trigonometrijskih jednadžbi cos x = a, sin x = a, tgx = a, ctg x = a.
Riješite jednadžbe (usmeno):
cos x = -1, sin x = 0, tgx = 0, ctg x = 1, cos x = 1,5, sin x = 0.
Pronađite pogreške i razmislite o uzrocima pogrešaka.
cos x = 1/2, x = +
/ 6 + 2k, k 
Z.
sin x = 3/2, x = / 3 + k, kZ.
tgx = / 4, x = 1 + k, kZ.
2. Učenje novog gradiva.
Ova lekcija će pokriti neke od najčešćih metoda za rješavanje trigonometrijskih jednadžbi.
Trigonometrijske jednadžbe svedene na kvadratne.
Ova klasa može uključivati jednadžbe koje uključuju jednu funkciju (sinus ili kosinus) ili dvije funkcije jednog argumenta, ali se jedna od njih svodi na drugu pomoću osnovnih trigonometrijskih identiteta.
Na primjer, ako je cosh uključen u jednadžbu u parnim potencijama, tada ga zamjenjujemo s 1- sin 2 x, ako je sin 2 x, onda ga zamjenjujemo s 1-cos 2 x.
Primjer.
Riješite jednadžbu: 8 sin 2 x - 6 sin x -5 = 0.
Rješenje: Označavamo sin x = t, tada je 8t 2 - 6t - 5 = 0,
D = 196,
T 1 = -1/2, t 2 = -5/4.
Izvršimo obrnutu promjenu i riješimo sljedeće jednadžbe.
X = (- 1) k + 1/6 + k, kZ.
Budući da je -5/4> 1, jednadžba nema korijena.
Odgovor: x = (- 1) k + 1/6 + k, kZ.
Rješenje vježbi jačanja.
Riješite jednadžbu:
1) 2sin 2 x + 3cos x = 0;
2) 5sin 2 x + 6cos x -6 = 0;
3) 2sin 2 x + 3cos 2 x = -2sin x;
4) 3 tg 2 x +2 tgx-1 = 0.
Homogene trigonometrijske jednadžbe.
Definicija: 1) Jednadžba oblikaa sinx + b cosx= 0, (a = 0, b = 0) naziva se homogena jednadžba prvog stupnja s obzirom na sin x i cos x.
Ova se jednadžba rješava tako da se oba njezina dijela podijele s cosx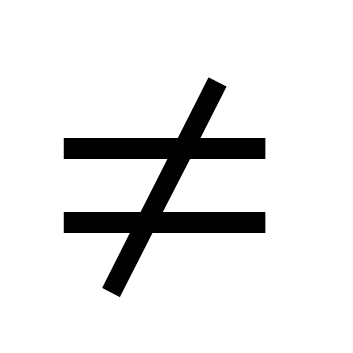 
0. Rezultat je jednadžba atgx + b = 0.
2) Jednadžba oblikaa grijeh 2 x + b sinx cosx + c cos 2 x =0 naziva se homogena jednadžba drugog stupnja, gdje su a, b, c bilo koji brojevi.
Ako je a = 0, tada se jednadžba rješava dijeljenjem oba dijela s cos 2 x 0. Kao rezultat dobivamo jednadžbu atg 2 x + btgx + c = 0.
Komentar: Jednadžba oblikaa grijeh mx + b cos mx=0 ili
a grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx =0 također su homogeni. Da bismo ih riješili, obje strane jednadžbe podijeljene su s cos mx=0 ili cos 2 mx=0
3) Različite jednadžbe se mogu svesti na homogene jednadžbe, koje u početku nisu takve. Na primjer,grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx = d, i a sinx + b cosx= d. Da biste riješili ove jednadžbe, trebate pomnožiti desnu stranu s "trigonometrijska jedinica" oni. na grijeh 2 x + cos 2 x i izvoditi matematičke transformacije.
Vježbe za konsolidaciju proučenog gradiva:
1) 2sin x- 3cos x = 0; 5) 4 sin 2 x - sin2x = 3;
2) sin 2x + cos2x = 0; 6) 3 sin 2 x + sinx cosx = 2 cos 2 x;
3) sin x + 3cos x = 0; 7) 3 sin 2 x- sinx cosx = 2;
4) sin 2 x -3 sinx cosx +2 cos 2 x = 0
3. Zbrajanje rezultata lekcije. Domaća zadaća.
U ovoj lekciji, ovisno o pripremljenosti grupe, možete razmotriti rješavanje jednadžbi oblika a sin mx + b cos mx = c, pri čemu a, b, c nisu u isto vrijeme jednaki nuli.
Vježbe za jačanje:
1,3sin x + cos x = 2;
2,3sin 2x + cos 2x = 2;
3.sin x / 3 + cos x / 3 = 1;
4.12 sin x +5 cos x + 13 = 0.
№ 3 Rješavanje trigonometrijskih jednadžbi
Cilj: 1) Proučiti način rješavanja trigonometrijskih jednadžbi faktorizacijom; naučiti rješavati trigonometrijske jednadžbe koristeći različite trigonometrijske formule;
2) Provjeriti: znanje učenika o formulama za rješavanje najjednostavnijih trigonometrijskih jednadžbi; sposobnost rješavanja najjednostavnijih trigonometrijskih jednadžbi.
Plan učenja:
Provjera domaće zadaće.
Matematički diktat.
Učenje novog gradiva.
Samostalan rad.
Zbrajanje rezultata lekcije. Domaća zadaća.
Tijek lekcije:
Provjera domaće zadaće (rješenje trigonometrijskih jednadžbi ukratko je napisano na ploči).
Matematički diktat.
U 1
1. Koje se jednadžbe nazivaju najjednostavnijim trigonometrijskim jednadžbama?
2. Kako se zove jednadžba oblikaa sinx + b cosx = 0? Molimo navedite način rješavanja.
3. Napišite formulu za korijene jednadžbe tgx = a(ctg x = a).
4. Zapišite formule za korijene jednadžbi oblika cosx = a, gdje a=1, a=0, a=-1.
5. Zapišite opću formulu za korijene jednadžbe sin x = a, | a|
6. Kako su jednadžbe oblikaa cosx = b, | b|
U 2
1. Zapišite formule za korijene jednadžbi cosx = a,| a|
2. Zapišite opću formulu za korijene jednadžbe
= a, | a|
3. Kako se zovu jednadžbe oblika sin x = a, tgx = a, sin x = a?
4. Zapišite formule za korijene jednadžbe sin x = a, ako a=1, a=0, a=-1.
5.Kako su jednadžbe oblika grijeh a x = b, | b|
6. Koje se jednadžbe nazivaju homogenim jednadžbama drugog stupnja? Kako se rješavaju?
Učenje novog gradiva.
Metoda faktoringa.
Jedna od najčešće korištenih metoda za rješavanje trigonometrijskih jednadžbi je metoda faktorizacije.
Ako se jednadžba f (x) = 0 može predstaviti kao f 1 (x) f 2 (x) = 0, tada se problem svodi na rješavanje dviju jednadžbi f 1 (x) = 0, f 2 (x) = 0 .
(Za učenike je korisno zapamtiti pravilo “ Umnožak faktora je nula ako je barem jedan od faktora nula, dok ostali imaju smisla»)
Konsolidacija proučenog gradiva kroz rješavanje jednadžbi različite složenosti.
(sin x-1/2) (sin x + 1) = 0; 2) (cosx- 2/2) (sin x + 2/2) = 0; (self)
3) sin 2 x + sin x cosx = 0; 4) sin 2 x - sin x = 0;
5) sin 2x - cosx = 0; 6) 4 cos 2 x -1 = 0; (Na 2 načina)
7) cosx + cos3x = 0; 8) sin 3x = sin 17x;
9) sin x + sin 2x + sin 3x = 0; 10) cos3x cos5x
11) sin x cos5x = sin 9x cos3x sin 2x sin 2x
12) 3 cosx sin x + cos 2 x = 0 (self)
13) 2 cos 2 x - sin (x- / 2) + tgx tg (x + / 2) = 0.
Samostalan rad.
Opcija-1 Opcija-2
1) 6 sin 2 x + 5sin x -1 = 0; 1) 3 cos 2 x + 2 cosx -5 = 0;
2) sin 2x - cos2x = 0; 2) 3 cos x / 2 - sin x / 2 = 0;
3) 5 sin 2 x + sin x cosx -2 cos 2 x = 2; 3) 4sin 2 x- sin x cosx + 7cos 2 x = 5;
4) sin x + sin5x = sin3x + sin7x; 4) sin x-sin 2x + sin 3x-sin 4x = 0;
5) sin x + cosx = 1. 5) sin x + cosx = 2.
8. Sažimanje lekcije. Domaća zadaća.
