कोज्या x समीकरण a के बराबर है। त्रिकोणमितीय समीकरण - सूत्र, समाधान, उदाहरण। गुणन

आप अपनी समस्या के विस्तृत समाधान का आदेश दे सकते हैं !!!

एक त्रिकोणमितीय फलन (`sin x, cos x, tan x` या` ctg x`) के चिह्न के तहत अज्ञात वाली समानता को त्रिकोणमितीय समीकरण कहा जाता है, और हम उनके सूत्रों पर आगे विचार करेंगे।

सरलतम समीकरणों को `sin x = a, cos x = a, tg x = a, ctg x = a` कहा जाता है, जहां `x` कोण है, `a` कोई भी संख्या है। आइए उनमें से प्रत्येक के लिए मूल सूत्र लिखें।

1. समीकरण `sin x = a`।

`| a |> 1` के लिए कोई समाधान नहीं है।

`| ए | . के लिए \ leq 1` के अनंत समाधान हैं।

मूल सूत्र: `x = (- 1) ^ n arcsin a + \ pi n, n \ in Z`

2. समीकरण `cos x = a`

`| a |> 1` के लिए - जैसा कि ज्या के मामले में होता है, वास्तविक संख्याओं के बीच इसका कोई हल नहीं होता है।

`| ए | . के लिए \ leq 1` के अनंत समाधान हैं।

मूल सूत्र: `x = \ pm arccos a + 2 \ pi n, n \ in Z`

रेखांकन में साइन और कोसाइन के लिए विशेष मामले।

3. समीकरण `tg x = a`

`ए` के किसी भी मान के लिए अनंत समाधान हैं।

मूल सूत्र: `x = arctan a + \ pi n, n \ in Z`

4. समीकरण `ctg x = a`

इसके अलावा `ए` के किसी भी मूल्य के लिए अनंत समाधान हैं।

मूल सूत्र: `x = arcctg a + \ pi n, n \ in Z`

एक तालिका में त्रिकोणमितीय समीकरणों की जड़ों के लिए सूत्र

साइन के लिए:
कोसाइन के लिए:
स्पर्शरेखा और कोटैंजेंट के लिए:
व्युत्क्रम त्रिकोणमितीय कार्यों वाले समीकरणों को हल करने के सूत्र:

त्रिकोणमितीय समीकरणों को हल करने के तरीके

किसी भी त्रिकोणमितीय समीकरण के हल में दो चरण होते हैं:

इसे सरलतम में परिवर्तित करके उपयोग करें;
उपरोक्त लिखित मूल सूत्रों और तालिकाओं का उपयोग करके परिणामी सरलतम समीकरण को हल करें।

आइए हल करने के मुख्य तरीकों के उदाहरण देखें।

बीजगणितीय विधि।

इस पद्धति में, चर प्रतिस्थापन और समानता में प्रतिस्थापन किया जाता है।

उदाहरण। समीकरण को हल करें: `2cos ^ 2 (x + \ frac \ pi 6) -3sin (\ frac \ pi 3 - x) + 1 = 0`

`2cos ^ 2 (x + \ frac \ pi 6) -3cos (x + \ frac \ pi 6) + 1 = 0`,

हम परिवर्तन करते हैं: `cos (x + \ frac \ pi 6) = y`, फिर` 2y ^ 2-3y + 1 = 0`,

हम मूल पाते हैं: `y_1 = 1, y_2 = 1/2`, जहां से दो मामले आते हैं:

1.` cos (x + \ frac \ pi 6) = 1`, `x + \ frac \ pi 6 = 2 \ pi n`,` x_1 = - \ frac \ pi 6 + 2 \ pi n`।

2.`cos (x + \ frac \ pi 6) = 1/2`, `x + \ frac \ pi 6 = \ pm arccos 1/2 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`।

उत्तर: `x_1 = - \ frac \ pi 6 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`।

गुणनखंडन।

उदाहरण। समीकरण को हल करें: `sin x + cos x = 1`।

समाधान। समानता के सभी पदों को बाईं ओर ले जाएँ: `sin x + cos x-1 = 0`। बाईं ओर का उपयोग, परिवर्तन और कारक:

`पाप x - 2sin ^ 2 x / 2 = 0`,

`2sin x / 2 cos x / 2-2sin ^ 2 x / 2 = 0`,

`2sin x/2 (cos x/2-sin x/2) = 0`,

`sin x/2 = 0`,` x/2 = \ pi n`, `x_1 = 2 \ pi n`।
`cos x/2-sin x/2 = 0`,` tg x/2 = 1`, `x/2 = arctan 1+ \ pi n`,` x/2 = \ pi / 4 + \ pi n` , `x_2 = \ pi / 2 + 2 \ pi n`।

उत्तर: `x_1 = 2 \ pi n`,` x_2 = \ pi/2 + 2 \ pi n`।

एक सजातीय समीकरण में कमी

सबसे पहले, आपको इस त्रिकोणमितीय समीकरण को दो प्रकारों में से एक में लाना होगा:

`a sin x + b cos x = 0` (पहली डिग्री का सजातीय समीकरण) या ` a sin ^ 2 x + b sin x cos x + c cos ^ 2 x = 0` (दूसरी डिग्री का सजातीय समीकरण)।

फिर दोनों भागों को पहले मामले के लिए `cos x \ ne 0` से विभाजित करें, और दूसरे के लिए `cos ^ 2 x \ ne 0` से विभाजित करें। हम `tg x`:` a tg x + b = 0` और `a tg ^ 2 x + b tg x + c = 0` के लिए समीकरण प्राप्त करते हैं, जिन्हें ज्ञात विधियों द्वारा हल करने की आवश्यकता होती है।

उदाहरण। समीकरण को हल करें: `2 sin ^ 2 x + sin x cos x - cos ^ 2 x = 1`।

समाधान। दाएँ पक्ष को `1 = sin ^ 2 x + cos ^ 2 x` के रूप में फिर से लिखें:

`2 sin ^ 2 x + sin x cos x - cos ^ 2 x =` पाप ^ 2 x + cos ^ 2 x`,

`2 पाप ^ 2 x + पाप x cos x - cos ^ 2 x -` पाप ^ 2 x - cos ^ 2 x = 0`

`पाप ^ 2 x + पाप x cos x - 2 cos ^ 2 x = 0`।

यह दूसरी डिग्री का एक समरूप त्रिकोणमितीय समीकरण है, हम इसके बाएँ और दाएँ पक्षों को `cos ^ 2 x \ ne 0` से विभाजित करते हैं, हमें मिलता है:

`\ frac (sin ^ 2 x) (cos ^ 2 x) + \ frac (sin x cos x) (cos ^ 2 x) - \ frac (2 cos ^ 2 x) (cos ^ 2 x) = 0`

`टीजी ^ 2 एक्स + टीजी एक्स - 2 = 0`। हम प्रतिस्थापन `tg x = t` का परिचय देते हैं, परिणामस्वरूप,` t ^ 2 + t - 2 = 0`। इस समीकरण के मूल हैं `t_1 = -2` तथा` t_2 = 1`। फिर:

`tg x = -2`,` x_1 = arctg (-2) + \ pi n`, `n \ in Z`
`tg x = 1`,` x = arctan 1+ \ pi n`, `x_2 = \ pi / 4 + \ pi n`,` n \ in Z`।

उत्तर। `x_1 = arctg (-2) + \ pi n`,` n \ in Z`, `x_2 = \ pi / 4 + \ pi n`,` n \ in Z`।

आधे कोने में जाओ

उदाहरण। समीकरण को हल करें: `11 sin x - 2 cos x = 10`।

समाधान। परिणाम के रूप में दोहरा कोण सूत्र लागू करें: `22 sin (x/2) cos (x/2) -` 2 cos ^ 2 x/2 + 2 sin ^ 2 x/2 =` `10 sin ^ 2 x / 2 +10 cos ^ 2 x / 2`

`4 टीजी ^ 2 एक्स/2 - 11 टीजी एक्स/2 + 6 = 0`

उपरोक्त बीजगणितीय विधि को लागू करने पर, हम प्राप्त करते हैं:

`tg x/2 = 2`,` x_1 = 2 आर्कटिक 2 + 2 \ pi n`, `n \ in Z`,
`tg x/2 = 3/4`,` x_2 = आर्कटिक 3/4 + 2 \ pi n`, `n \ in Z`।

उत्तर। `x_1 = 2 आर्कटन 2 + 2 \ pi n, n \ in Z`,` x_2 = arctan 3/4 + 2 \ pi n`, `n \ in Z`।

एक सहायक कोने का परिचय दें

त्रिकोणमितीय समीकरण में `a sin x + b cos x = c`, जहां a, b, c गुणांक हैं, और x एक चर है, हम दोनों पक्षों को ` sqrt (a ^ 2 + b ^ 2) से विभाजित करते हैं:

`\ फ्रैक ए (वर्ग (ए ^ 2 + बी ^ 2)) पाप एक्स +` \ फ्रैक बी (वर्ग (ए ^ 2 + बी ^ 2)) cos x = '' \ फ्रैक सी (वर्ग (ए ^ 2) + बी ^ 2)) `.

बाईं ओर के गुणांकों में साइन और कोसाइन के गुण होते हैं, अर्थात्, उनके वर्गों का योग 1 के बराबर होता है और उनके मापांक 1 से अधिक नहीं होते हैं। हम उन्हें निम्नानुसार दर्शाते हैं: \ frac a (sqrt (a ^ 2) + b ^ 2)) = cos \ varphi` , `\ frac b (sqrt (a ^ 2 + b ^ 2)) = sin \ varphi`,` \ frac c (sqrt (a ^ 2 + b ^ 2)) = सी`, फिर:

`cos \ varphi sin x + sin \ varphi cos x = C`।

आइए निम्नलिखित उदाहरण पर करीब से नज़र डालें:

उदाहरण। समीकरण को हल करें: `3 sin x + 4 cos x = 2`।

समाधान। समानता के दोनों पक्षों को `sqrt (3 ^ 2 + 4 ^ 2)` से विभाजित करें, हम प्राप्त करते हैं:

`\ फ़्रेक (3 पाप x) (वर्ग (3 ^ 2 + 4 ^ 2)) + `\ फ़्रेक (4 cos x) (वर्ग (3 ^ 2 + 4 ^ 2)) = '' \ फ़्रेक 2 (वर्ग) (3 ^ 2 + 4 ^ 2)) `

`3/5 पाप x + 4/5 cos x = 2/5`।

मान लीजिए `3/5 = cos \ varphi`,` 4/5 = sin \ varphi`। चूँकि `sin \ varphi> 0`,` cos \ varphi> 0`, तो हम `\ varphi = arcsin 4/5` को सहायक कोण के रूप में लेते हैं। तब हम अपनी समानता को रूप में लिखते हैं:

`cos \ varphi sin x + sin \ varphi cos x = 2/5`

ज्या के कोणों के योग के सूत्र को लागू करते हुए, हम अपनी समानता को निम्न रूप में लिखते हैं:

`पाप (x + \ varphi) = 2/5`,

`x + \ varphi = (- 1) ^ n आर्कसिन 2/5 + \ pi n`,` n \ in Z`,

`x = (- 1) ^ n आर्कसिन 2/5-` `arcsin 4/5 + \ pi n`,` n \ in Z`।

उत्तर। `x = (- 1) ^ n आर्कसिन 2/5-` `arcsin 4/5 + \ pi n`,` n \ in Z`।

भिन्नात्मक-तर्कसंगत त्रिकोणमितीय समीकरण

ये अंशों और हरों में त्रिकोणमितीय कार्यों के साथ अंशों के साथ समानताएं हैं।

उदाहरण। प्रश्न हल करें। `\ frac (sin x) (1 + cos x) = 1-cos x`।

समाधान। बराबरी के दाहिने हिस्से को `(1 + cos x)` से गुणा और भाग दें। परिणामस्वरूप, हमें मिलता है:

`\ frac (sin x) (1 + cos x) = '' \ frac ((1-cos x) (1 + cos x)) (1 + cos x)`

`\ frac (sin x) (1 + cos x) = `\ frac (1-cos ^ 2 x) (1 + cos x)`

`\ frac (sin x) (1 + cos x) =` \ frac (sin ^ 2 x) (1 + cos x)`

`\ frac (sin x) (1 + cos x) -` \ frac (sin ^ 2 x) (1 + cos x) = 0`

`\ frac (sin x-sin ^ 2 x) (1 + cos x) = 0`

यह मानते हुए कि हर शून्य के बराबर नहीं हो सकता, हमें मिलता है `1 + cos x \ ne 0`,` cos x \ ne -1`, `x \ ne \ pi + 2 \ pi n, n \ in Z`।

भिन्न के अंश को शून्य के बराबर करें: `sin x-sin ^ 2 x = 0`,` sin x (1-sin x) = 0`। फिर `sin x = 0` या `1-sin x = 0`।

`sin x = 0`,` x = \ pi n`, `n \ in Z`
`1-sin x = 0`,` sin x = -1`, `x = \ pi/2 + 2 \ pi n, n \ in Z`।

यह ध्यान में रखते हुए कि `x \ ne \ pi + 2 \ pi n, n \ in Z`, समाधान हैं `x = 2 \ pi n, n \ in Z` तथा `x = \ pi/2 + 2 \ pi n` , `n \ in Z`।

उत्तर। `x = 2 \ pi n`,` n \ in Z`, `x = \ pi/2 + 2 \ pi n`,` n \ in Z`।

त्रिकोणमिति, और विशेष रूप से त्रिकोणमितीय समीकरण, ज्यामिति, भौतिकी, इंजीनियरिंग के लगभग सभी क्षेत्रों में उपयोग किए जाते हैं। अध्ययन कक्षा 10 में शुरू होता है, परीक्षा के लिए निश्चित रूप से कार्य हैं, इसलिए त्रिकोणमितीय समीकरणों के सभी सूत्रों को याद रखने की कोशिश करें - वे निश्चित रूप से काम आएंगे!

हालाँकि, आपको उन्हें याद करने की भी आवश्यकता नहीं है, मुख्य बात यह है कि सार को समझना और उन्हें निकालने में सक्षम होना। यह उतना मुश्किल नहीं है जितना लगता है। वीडियो देखकर आप खुद ही देख लीजिए।

सबसे सरल त्रिकोणमितीय समीकरण आमतौर पर सूत्रों द्वारा हल किए जाते हैं। मैं आपको याद दिला दूं कि निम्नलिखित त्रिकोणमितीय समीकरणों को सरलतम कहा जाता है:

sinx = a

कॉसक्स = ए

टीजीएक्स = ए

सीटीजीएक्स = ए

x पाया जाने वाला कोण है,
ए - कोई भी संख्या।

और यहां वे सूत्र हैं जिनके साथ आप इन सरलतम समीकरणों के हल तुरंत लिख सकते हैं।

साइन के लिए:

कोसाइन के लिए:

х = ± आर्ककोस a + 2π n, n Z

स्पर्शरेखा के लिए:

एक्स = आर्कटन ए + π एन, एन ∈ जेड

कोटैंजेंट के लिए:

एक्स = आर्कसीटीजी ए + π एन, एन ∈ जेड

दरअसल, यह सबसे सरल त्रिकोणमितीय समीकरणों को हल करने का सैद्धांतिक हिस्सा है। इसके अलावा, सब कुछ!) कुछ भी नहीं। हालाँकि, इस विषय पर त्रुटियों की संख्या बहुत ही कम है। खासकर यदि उदाहरण टेम्पलेट से थोड़ा विचलित होता है। क्यों?

हाँ, क्योंकि बहुत से लोग इन पत्रों को लिखते हैं, उनका अर्थ बिल्कुल नहीं समझ रहे हैं!वह सावधानी से लिखता है, चाहे कुछ भी हो जाए ...) इससे निपटा जाना चाहिए। मनुष्यों के लिए त्रिकोणमिति, या त्रिकोणमिति के लिए मनुष्य आखिर!?)

क्या हम इसका पता लगाएंगे?

एक कोण के बराबर होगा आर्ककोस ए, दूसरा: -आर्कोस ए.

और यह हमेशा उसी तरह काम करेगा।किसी के लिए ए।

यदि आप मुझ पर विश्वास नहीं करते हैं, तो चित्र पर अपना माउस घुमाएँ, या टेबलेट पर चित्र को टैप करें।) मैंने नंबर बदल दिया है ए कुछ नकारात्मक को। वैसे भी, हमारे पास एक कोना है आर्ककोस ए, दूसरा: -आर्कोस ए.

इसलिए, उत्तर हमेशा जड़ों की दो श्रृंखलाओं के रूप में लिखा जा सकता है:

x 1 = आर्ककोस a + 2π n, n Z

x 2 = - चाप a + 2π n, n Z

हम इन दो श्रृंखलाओं को एक में जोड़ते हैं:

x = ± आर्ककोस a + 2π n, n Z

और बस यही। कोज्या के साथ सरलतम त्रिकोणमितीय समीकरण को हल करने के लिए एक सामान्य सूत्र प्राप्त करें।

यदि आप समझते हैं कि यह किसी प्रकार का अति-वैज्ञानिक ज्ञान नहीं है, बल्कि प्रतिक्रियाओं की दो श्रृंखलाओं का सिर्फ एक संक्षिप्त संकेतन,आप और कार्य "सी" कंधे पर होंगे। असमानताओं के साथ, दिए गए अंतराल से जड़ों के चयन के साथ ... वहाँ प्लस / माइनस के साथ उत्तर रोल नहीं करता है। और यदि आप उत्तर को व्यवसायिक तरीके से मानते हैं, और इसे दो अलग-अलग उत्तरों में विभाजित करते हैं, तो सब कुछ तय हो जाता है।) दरअसल, इसके लिए हम समझते हैं। क्या, कैसे और कहाँ।

सबसे सरल त्रिकोणमितीय समीकरण में

sinx = a

जड़ों की दो श्रृंखलाएँ भी प्राप्त होती हैं। हमेशा से रहा है। और इन दोनों सीरीज को रिकॉर्ड भी किया जा सकता है एक पंक्ति। केवल यह पंक्ति अधिक चालाक होगी:

х = (-1) n चाप a + n, n Z . पर

लेकिन सार वही रहता है। गणितज्ञों ने जड़ों की एक श्रृंखला के दो रिकॉर्ड के बजाय एक बनाने के लिए बस एक सूत्र का निर्माण किया। और बस!

आइए गणितज्ञों की जाँच करें? और फिर आप कभी नहीं जानते ...)

पिछले पाठ में, साइन के साथ त्रिकोणमितीय समीकरण के समाधान (बिना किसी सूत्र के) का विस्तार से विश्लेषण किया गया था:

उत्तर ने जड़ों की दो श्रृंखलाएँ उत्पन्न कीं:

एक्स 1 = / 6 + 2π एन, एन ∈ जेड

एक्स 2 = 5π / 6 + 2π एन, एन जेड

यदि हम सूत्र का उपयोग करके समान समीकरण को हल करते हैं, तो हमें उत्तर मिलता है:

x = (-1) n चाप 0.5 + n, n Z

दरअसल, यह एक अधूरा जवाब है।) छात्र को पता होना चाहिए कि आर्कसिन 0.5 = / 6।एक पूरा जवाब होगा:

एक्स = (-1) एन / 6+ एन, एन जेड

यह एक दिलचस्प सवाल उठाता है। के माध्यम से उत्तर दें एक्स 1; एक्स 2 (यह सही उत्तर है!) और अकेलेपन के माध्यम से एन एस (और यह सही उत्तर है!) - वही बात, या नहीं? हम अभी पता लगाएंगे।)

प्रत्युत्तर में प्रतिस्थापित करें एक्स 1 अर्थ एन = 0; 1; 2; और इसी तरह, हम गिनती करते हैं, हमें जड़ों की एक श्रृंखला मिलती है:

एक्स 1 = / 6; 13π / 6; 25π / 6 आदि।

उत्तर में समान प्रतिस्थापन के साथ एक्स 2 , हम पाते हैं:

एक्स 2 = 5π / 6; 17π / 6; 29π / 6 आदि।

अब हम मानों को प्रतिस्थापित करते हैं एन (0; 1; 2; 3; 4 ...) एन एस ... यही है, हम शून्य से एक को शून्य तक बढ़ाते हैं, फिर पहले, दूसरे, आदि तक। और, ज़ाहिर है, हम दूसरे कार्यकाल में 0 को प्रतिस्थापित करते हैं; 1; 2 3; 4, आदि और हम गिनते हैं। हमें श्रृंखला मिलती है:

एक्स = / 6; 5π / 6; 13π / 6; 17π / 6; 25π / 6 आदि।

आप बस इतना ही देख सकते हैं।) सामान्य सूत्र हमें देता है बिल्कुल वही परिणाम,दो उत्तरों के रूप में अलग-अलग। केवल एक ही बार में, क्रम में। गणितज्ञों के बहकावे में न आएं।)

त्रिकोणमितीय समीकरणों को स्पर्शरेखा और कोटैंजेंट के साथ हल करने के सूत्रों की भी जाँच की जा सकती है। लेकिन हम नहीं करेंगे।) वे बहुत सरल हैं।

मैंने इस सब प्रतिस्थापन और सत्यापन का उद्देश्य पर वर्णन किया है। यहां एक साधारण सी बात को समझना जरूरी है: प्राथमिक त्रिकोणमितीय समीकरणों को हल करने के लिए सूत्र हैं, उत्तरों का सिर्फ एक छोटा रिकॉर्ड।इस संक्षिप्तता के लिए, मुझे कोसाइन घोल में प्लस / माइनस और साइन घोल में (-1) n डालना था।

ये इंसर्ट उन कार्यों में किसी भी तरह से हस्तक्षेप नहीं करते हैं जहाँ आपको केवल एक प्राथमिक समीकरण का उत्तर लिखने की आवश्यकता होती है। लेकिन अगर आपको असमानता को हल करने की ज़रूरत है, या फिर आपको जवाब के साथ कुछ करने की ज़रूरत है: अंतराल पर जड़ों का चयन करें, ओडीजेड की जांच करें, आदि, ये आवेषण आसानी से किसी व्यक्ति को परेशान कर सकते हैं।

और क्या कर? हां, या तो उत्तर को दो श्रंखलाओं में लिखें, या त्रिकोणमितीय वृत्त के साथ समीकरण/असमानता को हल करें। तब ये इंसर्ट गायब हो जाते हैं और जीवन आसान हो जाता है।)

हम संक्षेप कर सकते हैं।

सरलतम त्रिकोणमितीय समीकरणों को हल करने के लिए तैयार उत्तर सूत्र हैं। चार टुकड़े। वे एक समीकरण के हल को तुरंत रिकॉर्ड करने के लिए अच्छे हैं। उदाहरण के लिए, आपको समीकरणों को हल करने की आवश्यकता है:

sinx = 0.3

सरलता: х = (-1) n चाप 0,3 + n, n Z

cosx = 0.2

कोई दिक्कत नहीं है: = ± आर्ककोस 0,2 + 2π n, n Z

टीजीएक्स = 1.2

सरलता: एक्स = आर्कटन 1,2 + π एन, एन ∈ जेड

सीटीजीएक्स = 3.7

एक बाकी: एक्स = आर्कसीटीजी3,7 + एन, एन ∈ जेड

कॉस एक्स = 1.8

यदि आप ज्ञान से जगमगाते हैं, तो तुरंत उत्तर लिखें:

x = ± आर्ककोस 1,8 + 2π n, n Z

तो आप पहले से ही चमक रहे हैं, यह ... वह ... पोखर से।) सही उत्तर: कोई समाधान नहीं। क्या आप समझते हैं क्यों? पढ़ें कि आर्ककोसाइन क्या है। इसके अलावा, यदि मूल समीकरण के दाईं ओर साइन, कोसाइन, टेंगेंट, कॉटेंजेंट के सारणीबद्ध मान हैं, - 1; 0; √3; 1/2; √3/2 आदि। - मेहराब के माध्यम से उत्तर अधूरा होगा। मेहराब का रेडियन में अनुवाद किया जाना चाहिए।

और अगर आपके सामने असमानता आती है जैसे

तो उत्तर है:

n, n Z

एक दुर्लभ बकवास है, हाँ ...) यहाँ त्रिकोणमितीय वृत्त पर निर्णय लेना आवश्यक है। हम प्रासंगिक विषय में क्या करेंगे।

उन लोगों के लिए जिन्होंने वीरतापूर्वक इन पंक्तियों को पढ़ा है। मैं आपकी मदद नहीं कर सकता, लेकिन आपके टाइटैनिक प्रयासों की सराहना करता हूं। आप एक बोनस।)

बक्शीश:

एक खतरनाक युद्ध के माहौल में सूत्र लिखते समय, अकादमिक रूप से कठोर नर्ड भी अक्सर भ्रमित हो जाते हैं कि कहाँ n, और कहाँ 2π एन. यहाँ एक सरल तरकीब है। में के सभीफ़ार्मुलों लायक n. व्युत्क्रम कोसाइन वाले एकमात्र सूत्र को छोड़कर। यह वहीं खड़ा है 2πn. दोपीन कीवर्ड - दो।एक ही सूत्र में शामिल हैं दोशुरुआत में हस्ताक्षर करें। प्लस और माइनस। इधर - उधर - दो।

तो अगर आपने लिखा दोव्युत्क्रम कोसाइन के सामने साइन इन करें, यह याद रखना आसान है कि अंत में क्या होगा दोपीन और यहां तक कि विपरीत होता है। स्किप मैन साइन ± , अंत तक पहुँचता है, ठीक लिखता है दोपीन, और यह अपने होश में आ जाएगा। कुछ आगे दोसंकेत! व्यक्ति शुरुआत में लौट आएगा, लेकिन वह गलती को सुधारेगा! इस कदर।)

अगर आपको यह साइट पसंद है ...

वैसे, मेरे पास आपके लिए कुछ और दिलचस्प साइटें हैं।)

आप उदाहरणों को हल करने का अभ्यास कर सकते हैं और अपने स्तर का पता लगा सकते हैं। त्वरित सत्यापन परीक्षण। सीखना - रुचि के साथ!)

आप कार्यों और डेरिवेटिव से परिचित हो सकते हैं।

ज़खारोवा लुडमिला व्लादिमीरोवना
बरनौल में MBOU "माध्यमिक विद्यालय नंबर 59"
गणित शिक्षक [ईमेल संरक्षित]

№1 सरलतम त्रिकोणमितीय समीकरण

लक्ष्य: 1. फॉर्म के सबसे सरल त्रिकोणमितीय समीकरणों के समाधान के लिए सूत्र प्राप्त करें sinx = a, cosx = a, tgx = a, ctgx = a;

2. सूत्रों का उपयोग करके सरलतम त्रिकोणमितीय समीकरणों को हल करना सीखें।

उपकरण: 1) त्रिकोणमितीय फलनों के रेखांकन वाली सारणी y = sinx, y = cosx, y = tgx, y = ctgx; 2) व्युत्क्रम त्रिकोणमितीय कार्यों के मूल्यों की तालिका; 3) सरलतम त्रिकोणमितीय समीकरणों को हल करने के लिए सूत्रों की सारांश तालिका।

व्याख्यान पाठ योजना:

1 समीकरण की जड़ों के लिए सूत्रों की व्युत्पत्ति

ए) sinx = ए,

बी) कॉक्स = ए,

सी) टीजीएक्स = ए,

डी) सीटीजीएक्स = ए.

2 ... प्राप्त सूत्रों को समेकित करने के लिए मौखिक ललाट कार्य।

3 ... अध्ययन सामग्री को समेकित करने के लिए लिखित कार्य

कक्षाओं के दौरान।

बीजगणित, ज्यामिति, भौतिकी और अन्य विषयों में हमें कई तरह की समस्याओं का सामना करना पड़ता है, जिनका समाधान समीकरणों के समाधान से जुड़ा होता है। हमने त्रिकोणमितीय फलनों के गुणों का अध्ययन किया है, इसलिए उन समीकरणों की ओर मुड़ना स्वाभाविक है जिनमें फलनों के चिह्न के अंतर्गत अज्ञात निहित है।

परिभाषा: फॉर्म के समीकरण sinx = ए , cosx= ए , टीजीएक्स= ए , सीटीजीएक्स= ए सरलतम त्रिकोणमितीय समीकरण कहलाते हैं।

सबसे सरल त्रिकोणमितीय समीकरणों को हल करना सीखना बहुत महत्वपूर्ण है, क्योंकि किसी भी त्रिकोणमितीय समीकरणों को हल करने के लिए सभी विधियों और तकनीकों को उन्हें सरलतम तक कम करना है।

आइए सूत्र प्राप्त करके प्रारंभ करें जो त्रिकोणमितीय समीकरणों को हल करते समय "सक्रिय रूप से" काम करते हैं।

1. sinx के रूप के समीकरण = ए.

आइए समीकरण को हल करें sinx = एग्राफिक रूप से। ऐसा करने के लिए, एक समन्वय प्रणाली में, हम फ़ंक्शन y = sinx और y = . के ग्राफ़ प्लॉट करते हैं ए।

1) अगर ए> 1 और एपापएक्स = एकोई समाधान नहीं है, क्योंकि सीधी रेखा और साइनसॉइड में कोई बिंदु समान नहीं है।

2) यदि -1a a साइनसॉइड को अनंत रूप से कई बार पार करता है। इसका मतलब है कि समीकरण sinx = एअसीम रूप से कई समाधान हैं।

चूंकि ज्या की अवधि 2 . है , फिर समीकरण को हल करने के लिए sinx = एलंबाई 2 के किसी भी खंड पर सभी समाधान खोजने के लिए पर्याप्त है।

[- / 2 के लिए समीकरण को हल करके; / 2] आर्क्सिन x = . की परिभाषा के अनुसारआर्कसिन ए, और x = -arcsin . पर ए... फलन y = sinx की आवर्तता को ध्यान में रखते हुए, हम निम्नलिखित व्यंजक प्राप्त करते हैं:

एक्स = -आर्क्सिन ए+ 2एन, एन जेड।

समाधानों की दोनों श्रृंखलाओं को जोड़ा जा सकता है

एक्स = (-1) एन आर्क्सिन ए+ एन, एनजेड।

निम्नलिखित तीन मामलों में, वे सामान्य सूत्र नहीं, बल्कि सरल संबंधों का उपयोग करना पसंद करते हैं:

अगर ए= -1, तो पाप x = -1, x = - / 2 + 2n

अगर ए= 1, तो पाप x = 1, x = / 2 + 2n

अगर ए = 0, फिर पाप x = 0। एक्स = एन,

उदाहरण: समीकरण हल करें sinx = 1/2.

आइए समाधानों के लिए सूत्र तैयार करें x = चाप 1/2 + 2n

एक्स = - चाप a + 2n

आइए मान की गणना करेंआर्क्सिन1 / 2। पाए गए मान को समाधान फ़ार्मुलों में बदलें

एक्स = 5/6 + 2 एन

या सामान्य सूत्र द्वारा

एक्स = (-1) एन आर्क्सिन 1/2 + एन,

एक्स = (-1) एन / 6 + एन,

2. फॉर्म के समीकरण कॉसक्स = ए.

आइए समीकरण को हल करें cosx = एरेखीय रूप से भी, फलन y = cosx और y = . के आलेखों को आलेखित करना ए.

1) यदि 1, तो समीकरणकॉसक्स = एइसका कोई हल नहीं है, क्योंकि ग्राफ़ में उभयनिष्ठ बिंदु नहीं होते हैं।

2) अगर -1 एकॉसक्स = एसमाधान की अनंत संख्या है।

हम सभी समाधान खोज लेंगेकॉसक्स = एलंबाई 2 के अंतराल पर क्योंकि कोज्या का आवर्त 2 है।

आर्ककोसाइन की परिभाषा के अनुसार समीकरण के हल पर x = . होगाआर्कोस ए. कोज्या फलन की समता को देखते हुए [-; 0] पर समीकरण का हल x = -arcos होगा ए.

इस प्रकार, समीकरण के हलकॉसक्स = एएक्स = + आर्कोस ए+ 2 एन,

तीन मामलों में, हम एक सामान्य सूत्र का नहीं, बल्कि सरल संबंधों का उपयोग करेंगे:

अगर ए= -1, फिर cosx = -1, x = - / 2 + 2n

अगर ए= 1, तो cosx = 1, x = 2n,

यदि a = 0, तो cosx = 0। एक्स = / 2 + एन

उदाहरण: समीकरण हल करेंकॉस एक्स = 1/2,

आइए समाधानों के लिए सूत्र तैयार करें x = चाप 1/2 + 2n

आइए मान की गणना करेंआर्ककोस1 / 2।

पाए गए मान को समाधान फ़ार्मुलों में बदलें

एक्स = + /3+ 2एन, एनजेड।

फॉर्म के समीकरण टीजीएक्स = ए.

चूँकि स्पर्श रेखा का आवर्त समान होता है, तो समीकरण के सभी हल ज्ञात करने के लिएटीजीएक्स = ए, लंबाई के किसी भी अंतराल पर सभी समाधान खोजने के लिए पर्याप्त है। आर्कटिक की परिभाषा के अनुसार, (- / 2; / 2) पर समीकरण का हल आर्कटिक है ए. फ़ंक्शन की अवधि को ध्यान में रखते हुए, समीकरण के सभी समाधानों को रूप में लिखा जा सकता है

एक्स = आर्कटजी ए+ एन, एनजेड।

उदाहरण:प्रश्न हल करेंटीजी एक्स = 3/3

आइए x = . को हल करने के लिए एक सूत्र बनाते हैंआर्कटिक 3/3 + एन, एनजेड।

हम आर्कटिक के मान की गणना करते हैंआर्कटिक 3/3 = / 6, तब

एक्स = / 6 + एन, एनजेड।

एक समीकरण को हल करने के लिए एक सूत्र की व्युत्पत्ति साथ टीजीएक्स= एछात्रों को प्रदान किया जा सकता है।

उदाहरण।

प्रश्न हल करेंसीटीजी एक्स = 1.

x = चाप 1 + n, nZ,

एक्स = / 4 + एन, एनजेड।

अध्ययन की गई सामग्री के परिणामस्वरूप, छात्र तालिका भर सकते हैं:

"त्रिकोणमितीय समीकरणों को हल करना।"

समीकरण

अध्ययन की गई सामग्री को समेकित करने के लिए अभ्यास।

(मौखिक रूप से) कौन सा लिखित समीकरण सूत्रों द्वारा हल किया जा सकता है:

ए) एक्स = (-1) एन आर्क्सिन ए+ एन, एनजेड;

बी) एक्स = + आर्कोस ए + 2 एन?

cos x = 2/2, tg x = 1, sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 ...

सूचीबद्ध समीकरणों में से किसका कोई हल नहीं है?

समीकरण हल करें:

ए) पाप एक्स = 0; ई) पाप एक्स = 2/2; एच) पाप एक्स = 2;

बी) कॉस एक्स = 2/2; च) क्योंकि x = -1/2; i) कॉस एक्स = 1;

डी) टीजी एक्स = 3; छ) सीटीजी एक्स = -1; जे) टीजी एक्स = 1/3।

3. समीकरणों को हल करें:

ए) पाप 3x = 0; ई) 2cos x = 1;

बी) कॉस एक्स / 2 = 1/2; च) 3 तन 3x = 1;

डी) पाप एक्स / 4 = 1; छ) 2cos (2x +/5) = 3.

इन समीकरणों को हल करते समय, फॉर्म के समीकरणों को हल करने के नियमों को लिखना उपयोगी होता हैपाप वीएक्स = ए, तथा साथपाप वीएक्स = ए, | ए|1.

पाप वीएक्स = ए, | ए | 1.

वीएक्स = (-1) एन आर्क्सिन ए+ एन, एनजेड,

एक्स = (-1) एन 1 / वीआर्कसिन ए+ एन / वी, न्यूजीलैंड

पाठ के परिणामों का सारांश:

आज के पाठ में हमने सरलतम त्रिकोणमितीय समीकरणों को हल करने के सूत्र निकाले हैं।

सरलतम त्रिकोणमितीय समीकरणों को हल करने के उदाहरण।

हमने उस तालिका को भरा है जिसका उपयोग हम समीकरणों को हल करने के लिए करेंगे।

होम वर्क।

№2 त्रिकोणमितीय समीकरणों को हल करना

लक्ष्य: त्रिकोणमितीय समीकरणों को हल करने के तरीकों का अध्ययन करने के लिए: 1) द्विघात से द्विघात; 2) समरूप त्रिकोणमितीय समीकरणों को कम करने योग्य।

त्रिकोणमितीय समीकरणों को हल करने के विभिन्न तरीकों का उपयोग करते समय छात्रों के अवलोकन कौशल का विकास करना।

छात्रों के साथ फ्रंटल वर्क.

त्रिकोणमितीय समीकरणों की जड़ों के लिए सूत्र क्या हैंकॉस एक्स = ए, पाप x = ए, टीजीएक्स = ए, सीटीजी एक्स = ए.

समीकरणों को हल करें (मौखिक रूप से):

cos x = -1, sin x = 0, tgx = 0, ctg x = 1, cos x = 1.5, sin x = 0।

त्रुटियों का पता लगाएं और त्रुटियों के कारणों के बारे में सोचें।

कॉस x = 1/2, x = + / 6 + 2k, k जेड

पाप एक्स = 3/2, एक्स = / 3 + के, केजेड।

टीजीएक्स = / 4, एक्स = 1 + के, केजेड।

2. नई सामग्री सीखना।

इस पाठ में त्रिकोणमितीय समीकरणों को हल करने के कुछ सबसे सामान्य तरीकों को शामिल किया जाएगा।

त्रिकोणमितीय समीकरणों को द्विघात में घटाया गया।

इस वर्ग में ऐसे समीकरण शामिल हो सकते हैं जिनमें एक फ़ंक्शन (साइन या कोसाइन) या एक तर्क के दो फ़ंक्शन शामिल होते हैं, लेकिन उनमें से एक को मूल त्रिकोणमितीय पहचान का उपयोग करके दूसरे में घटा दिया जाता है।

उदाहरण के लिए, यदि cоsх को सम घातों में समीकरण में शामिल किया जाता है, तो हम इसे 1- sin 2 x से बदल देते हैं, यदि sin 2 x, तो हम इसे 1-cos 2 x से बदल देते हैं।

उदाहरण।

समीकरण हल करें: 8पाप 2 x - 6 पाप x -5 = 0.

हल: हम निरूपित करते हैंपाप x = t, फिर 8t 2 - 6t - 5 = 0,

डी = 196,

टी 1 = -1/2, टी 2 = -5/4।

आइए विपरीत परिवर्तन करते हैं और निम्नलिखित समीकरणों को हल करते हैं।

एक्स = (- 1) के + 1/6 + के, केजेड।

चूंकि -5/4> 1 समीकरण का कोई मूल नहीं है।

उत्तर: x = (- 1) k + 1/6 + k, kZ।

व्यायाम को मजबूत करने का समाधान।

प्रश्न हल करें:

1) 2sin 2 x + 3cos x = 0;

2) 5sin 2 x + 6cos x -6 = 0;

3) 2sin 2 x + 3cos 2 x = -2sin x;

4) 3 टीजी 2 एक्स +2 टीजीएक्स -1 = 0।

सजातीय त्रिकोणमितीय समीकरण।

परिभाषा: 1) फॉर्म का समीकरणए sinx + बी cosx= 0, (ए = 0, बी = 0) sin x और cos x के सन्दर्भ में प्रथम घात का सजातीय समीकरण कहलाता है।

इस समीकरण को इसके दोनों भागों को से विभाजित करके हल किया जाता है cosx 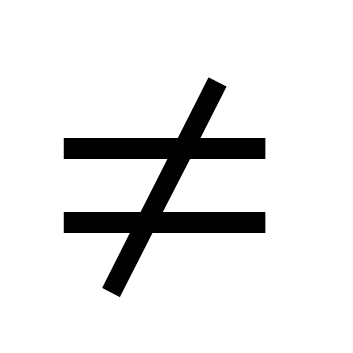0. परिणाम समीकरण हैएटीजीएक्स + बी = 0।

2) फॉर्म का एक समीकरणए पाप 2 एक्स + बी sinx cosx + सी क्योंकि 2 एक्स =0 दूसरी डिग्री का सजातीय समीकरण कहलाता है, जहाँ a, b, c कोई भी संख्या है।

यदि a = 0 है, तो दोनों भागों को से विभाजित करके समीकरण हल किया जाता हैक्योंकि 2 x 0. परिणामस्वरूप, हम समीकरण प्राप्त करते हैंएटीजी 2 एक्स + बीटीजीएक्स + सी = 0।

टिप्पणी:फॉर्म का समीकरणए पाप एमएक्स + बी क्योंकि एमएक्स=0 या

ए पाप 2 एमएक्स + बी पाप एमएक्स क्योंकि एमएक्स + सी क्योंकि 2 एमएक्स =0 सजातीय भी हैं। उन्हें हल करने के लिए, समीकरण के दोनों पक्षों को cos . से विभाजित किया जाता है एमएक्स=0 या क्योंकि 2 एमएक्स=0

3) विभिन्न समीकरणों को समांगी समीकरणों में घटाया जा सकता है, जो प्रारंभ में ऐसे नहीं होते हैं। उदाहरण के लिए,पाप 2 एमएक्स + बी पाप एमएक्स क्योंकि एमएक्स + सी क्योंकि 2 एमएक्स = डी, तथा ए sinx + बी cosx= डी. इन समीकरणों को हल करने के लिए, आपको दाईं ओर से गुणा करना होगा "त्रिकोणमितीय इकाई"वे। पर पाप 2 एक्स + क्योंकि 2 एक्सऔर गणितीय परिवर्तन करते हैं।

अध्ययन की गई सामग्री को समेकित करने के लिए अभ्यास:

1) 2sin x- 3cos x = 0; 5) 4 पाप 2 एक्स - पाप 2 एक्स = 3;

2) sin 2x + cos2x = 0; 6) 3 पाप 2 x + sinx cosx = 2 cos 2 x;

3) sin x + 3cos x = 0; 7) 3 sin 2 x- sinx cosx = 2;

4) sin 2 x -3 sinx cosx +2 cos 2 x = 0

3. पाठ के परिणामों का सारांश। होम वर्क।

इस पाठ में, समूह की तैयारी के आधार पर, आप फॉर्म के समीकरणों को हल करने पर विचार कर सकते हैं a sin mx + b cos mx = c, जहाँ a, b, c एक ही समय में शून्य के बराबर नहीं हैं।

व्यायाम को मजबूत बनाना:

1.3sin x + cos x = 2;

2.3sin 2x + cos 2x = 2;

3.sin x / 3 + cos x / 3 = 1;

4.12 sin x +5 cos x + 13 = 0.

№ 3 त्रिकोणमितीय समीकरणों को हल करना

लक्ष्य: 1) गुणनखंडन द्वारा त्रिकोणमितीय समीकरणों को हल करने की विधि का अध्ययन करें; विभिन्न त्रिकोणमितीय सूत्रों का उपयोग करके त्रिकोणमितीय समीकरणों को हल करना सीखें;

2) जाँच करें: सरलतम त्रिकोणमितीय समीकरणों को हल करने के लिए छात्रों के सूत्रों का ज्ञान; सरलतम त्रिकोणमितीय समीकरणों को हल करने की क्षमता।

पाठ योजना:

होमवर्क की जाँच।

गणितीय श्रुतलेख।

नई सामग्री सीखना।

स्वतंत्र काम।

पाठ के परिणामों का सारांश। होम वर्क।

पाठ का कोर्स:

होमवर्क चेक (त्रिकोणमितीय समीकरणों का हल संक्षेप में ब्लैकबोर्ड पर लिखा गया है)।

गणितीय श्रुतलेख।

पहले में

1. सबसे सरल त्रिकोणमितीय समीकरण कौन से समीकरण कहलाते हैं?

2. फॉर्म के समीकरण का नाम क्या हैए sinx + बीकॉसक्स = 0? कृपया इसे हल करने का तरीका बताएं।

3.समीकरण के मूलों का सूत्र लिखिएटीजीएक्स = ए(सीटीजी एक्स = ए).

4. फॉर्म के समीकरणों की जड़ों के लिए सूत्र लिखिएकॉसक्स = ए, कहां ए=1, ए=0, ए=-1.

5. समीकरण के मूलों का सामान्य सूत्र लिखिएपाप x = ए, | ए|

6. फॉर्म के समीकरण कैसे होते हैंएकॉसक्स = बी, | बी|

मे 2

1. समीकरणों के मूलों के सूत्र लिखिएकॉसक्स = ए,| ए|

2. समीकरण के मूलों का सामान्य सूत्र लिखिए

= ए, | ए|

3. फॉर्म के समीकरणों के नाम क्या हैंपाप x = ए, टीजीएक्स = ए, पाप x = ए?

4. समीकरण के मूलों के सूत्र लिखिएपाप x = ए, अगर ए=1, ए=0, ए=-1.

5.रूप के समीकरण कैसे होते हैंपाप एएक्स = बी, | बी|

6. किन समीकरणों को द्वितीय कोटि के समांगी समीकरण कहते हैं? उनका समाधान कैसे किया जाता है?

नई सामग्री सीखना।

फैक्टरिंग विधि।

त्रिकोणमितीय समीकरणों को हल करने के लिए सबसे अधिक इस्तेमाल की जाने वाली विधियों में से एक गुणन विधि है।

यदि समीकरण f (x) = 0 को f 1 (x) f 2 (x) = 0 के रूप में दर्शाया जा सकता है, तो समस्या दो समीकरणों को हल करने के लिए कम हो जाती है f 1 (x) = 0, f 2 (x) = 0 .

(छात्रों के साथ, नियम को याद रखना सहायक होता है " कारकों का गुणनफल शून्य है यदि कम से कम एक कारक शून्य है, जबकि अन्य का अर्थ है»)

विभिन्न जटिलता के समीकरणों के समाधान के माध्यम से अध्ययन की गई सामग्री का समेकन।

(पाप x-1/2) (पाप x + 1) = 0; 2) (cosx- 2/2) (पाप x + 2/2) = 0; (स्वयं)

3) पाप 2 x + पाप x cosx = 0; 4) पाप 2 एक्स - पाप एक्स = 0;

5) पाप 2x - cosx = 0; 6) 4 cos 2 x -1 = 0; (2 तरीकों से)

7) cosx + cos3x = 0; 8) पाप 3x = पाप 17x;

9) पाप x + पाप 2x + पाप 3x = 0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x + cos 2 x = 0 (स्वयं)

13) 2 cos 2 x - sin (x- / 2) + tgx tg (x + / 2) = 0.

स्वतंत्र काम।

विकल्प -1 विकल्प -2

1) 6 पाप 2 x + 5पाप x -1 = 0; 1) 3 cos 2 x + 2 cosx -5 = 0;

2) पाप 2x - cos2x = 0; 2) 3 कॉस एक्स / 2 - पाप एक्स / 2 = 0;

3) 5 sin 2 x + sin x cosx -2 cos 2 x = 2; 3) 4sin 2 x- sin x cosx + 7cos 2 x = 5;

4) पाप x + sin5x = sin3x + sin7x; 4) sin x-sin 2x + sin 3x-sin 4x = 0;

5) पाप x + cosx = 1. 5) पाप x + cosx = 2।

8. पाठ को सारांशित करना। होम वर्क।