Косинусот x равенката е еднаква на a. Тригонометриски равенки - формули, решенија, примери. Факторизација

Можете да нарачате детално решение за вашиот проблем !!!

Еднаквоста што содржи непозната под знакот на тригонометриска функција (`sin x, cos x, tan x` или` ctg x`) се нарекува тригонометриска равенка, а ние понатаму ќе ги разгледаме нивните формули.

Наједноставните равенки се нарекуваат `sin x = a, cos x = a, tg x = a, ctg x = a`, каде што` x` е аголот што треба да се најде, „a“ е кој било број. Ајде да ги запишеме коренските формули за секоја од нив.

1. Равенка `sin x = a`.

За `| a |> 1` нема решенија.

За `| a | \ leq 1` има бесконечен број решенија.

Формула на коренот: `x = (- 1) ^ n arcsin a + \ pi n, n \ во Z`

2. Равенката `cos x = a`

За `| a |> 1` - како и во случајот со синус, тој нема решенија меѓу реалните броеви.

За `| a | \ leq 1` има бесконечен број решенија.

Формула на коренот: `x = \ pm arccos a + 2 \ pi n, n \ во Z`

Посебни случаи за синус и косинус во графикони.

3. Равенката `tg x = a`

Има бесконечен број решенија за која било вредност на `a`.

Формула на коренот: `x = арктан a + \ pi n, n \ во Z`

4. Равенка `ctg x = a`

Исто така, има бесконечен број решенија за сите вредности на `a`.

Формула на коренот: `x = arcctg a + \ pi n, n \ во Z`

Формули за корени на тригонометриски равенки во табела

За синус:
За косинус:
За тангента и котангента:
Формули за решавање равенки кои содржат инверзни тригонометриски функции:

Методи за решавање на тригонометриски равенки

Решението на која било тригонометриска равенка се состои од две фази:

• користејќи го конвертирај во наједноставниот;
• решете ја добиената наједноставна равенка користејќи ги горенаведените напишани коренски формули и табели.

Да ги погледнеме примерите на главните методи на решавање.

Алгебарски метод.

Во овој метод се врши замена на променливата и замена во еднаквост.

Пример. Решете ја равенката: `2cos ^ 2 (x + \ frac \ pi 6) -3sin (\ frac \ pi 3 - x) + 1 = 0`

`2cos ^ 2 (x + \ frac \ pi 6) -3cos (x + \ frac \ pi 6) + 1 = 0`,

ја правиме промената: `cos (x + \ frac \ pi 6) = y`, потоа` 2y ^ 2-3y + 1 = 0`,

ги наоѓаме корените: `y_1 = 1, y_2 = 1 / 2`, од каде следат два случаи:

1.` cos (x + \ frac \ pi 6) = 1`, `x + \ frac \ pi 6 = 2 \ pi n`,` x_1 = - \ frac \ pi 6 + 2 \ pi n`.

2.` cos (x + \ frac \ pi 6) = 1 / 2`, `x + \ frac \ pi 6 = \ pm arccos 1/2 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`.

Одговор: `x_1 = - \ frac \ pi 6 + 2 \ pi n`,` x_2 = \ pm \ frac \ pi 3- \ frac \ pi 6 + 2 \ pi n`.

Факторизација.

Пример. Решете ја равенката: `sin x + cos x = 1`.

Решение. Поместете ги сите членови на еднаквоста налево: `sin x + cos x-1 = 0`. Користење, трансформирање и факторинг на левата страна:

`sin x - 2sin ^ 2 x / 2 = 0`,

`2sin x / 2 cos x / 2-2sin ^ 2 x / 2 = 0`,

`2 sin x / 2 (cos x / 2-sin x / 2) = 0`,

1. `sin x / 2 = 0`,` x / 2 = \ pi n`, `x_1 = 2 \ pi n`.
2. `cos x / 2-sin x / 2 = 0`,` tg x / 2 = 1`, `x / 2 = арктан 1+ \ pi n`,` x / 2 = \ pi / 4 + \ pi n` , `x_2 = \ pi / 2 + 2 \ pi n`.

Одговор: `x_1 = 2 \ pi n`,` x_2 = \ pi / 2 + 2 \ pi n`.

Намалување на хомогена равенка

Прво, треба да ја доведете оваа тригонометриска равенка на еден од двата вида:

`a sin x + b cos x = 0` (хомогена равенка од прв степен) или` a sin ^ 2 x + b sin x cos x + c cos ^ 2 x = 0` (хомогена равенка од втор степен).

Потоа поделете ги двата дела со `cos x \ ne 0` - за првиот случај, и со` cos ^ 2 x \ ne 0` - за вториот. Добиваме равенки за `tg x`:` a tg x + b = 0` и `a tg ^ 2 x + b tg x + c = 0`, кои треба да се решат со познати методи.

Пример. Решете ја равенката: `2 sin ^ 2 x + sin x cos x - cos ^ 2 x = 1`.

Решение. Препишете ја десната страна како `1 = грев ^ 2 x + cos ^ 2 x`:

`2 грев ^ 2 x + грев x cos x - cos ^ 2 x =` `грев ^ 2 x + cos ^ 2 x`,

`2 грев ^ 2 x + грев x cos x - cos ^ 2 x -` `грев ^ 2 x - cos ^ 2 x = 0`

`грев ^ 2 x + грев x cos x - 2 cos ^ 2 x = 0`.

Ова е хомогена тригонометриска равенка од втор степен, ја делиме нејзината лева и десна страна со `cos ^ 2 x \ ne 0`, добиваме:

`\ frac (sin ^ 2 x) (cos ^ 2 x) + \ frac (sin x cos x) (cos ^ 2 x) - \ frac (2 cos ^ 2 x) (cos ^ 2 x) = 0`

`tg ^ 2 x + tg x - 2 = 0`. Воведуваме замена `tg x = t`, како резултат на тоа,` t ^ 2 + t - 2 = 0`. Корените на оваа равенка се `t_1 = -2` и` t_2 = 1`. Потоа:

1. `tg x = -2`,` x_1 = arctg (-2) + \ pi n`, `n \ во Z`
2. `tg x = 1`,` x = арктан 1+ \ pi n`, `x_2 = \ pi / 4 + \ pi n`,` n \ во Z`.

Одговори. `x_1 = arctg (-2) + \ pi n`,` n \ во Z`, `x_2 = \ pi / 4 + \ pi n`,` n \ во Z`.

Одете на половина агол

Пример. Решете ја равенката: `11 sin x - 2 cos x = 10`.

Решение. Примени ги формулите за двоен агол, како резултат: `22 sin (x / 2) cos (x / 2) -`` 2 cos ^ 2 x / 2 + 2 sin ^ 2 x / 2 =` `10 sin ^ 2 x / 2 +10 cos ^ 2 x / 2`

`4 tg ^ 2 x / 2 - 11 tg x / 2 + 6 = 0`

Применувајќи го горенаведениот алгебарски метод, добиваме:

1. `tg x / 2 = 2`,` x_1 = 2 арктан 2 + 2 \ pi n`, `n \ во Z`,
2. `tg x / 2 = 3 / 4`,` x_2 = арктан 3/4 + 2 \ pi n`, `n \ во Z`.

Одговори. `x_1 = 2 арктан 2 + 2 \ pi n, n \ во Z`,` x_2 = арктан 3/4 + 2 \ pi n`, `n \ во Z`.

Воведете помошен агол

Во тригонометриската равенка `a sin x + b cos x = c`, каде што a, b, c се коефициенти и x е променлива, ги делиме двете страни со` sqrt (a ^ 2 + b ^ 2) `:

`\ frac a (sqrt (a ^ 2 + b ^ 2)) sin x +` `\ frac b (sqrt (a ^ 2 + b ^ 2)) cos x = '' \ frac c (sqrt (a ^ 2 + b ^ 2)) `.

Коефициентите од левата страна имаат својства на синус и косинус, имено, збирот на нивните квадрати е еднаков на 1, а нивните апсолутни вредности не се поголеми од 1. Ги означуваме на следниов начин: `\ frac a (sqrt ( a ^ 2 + b ^ 2)) = cos \ varphi` , `\ frac b (sqrt (a ^ 2 + b ^ 2)) = sin \ varphi`,` \ frac c (sqrt (a ^ 2 + b ^ 2)) = C`, тогаш:

`cos \ varphi sin x + sin \ varphi cos x = C`.

Да го разгледаме подетално следниот пример:

Пример. Решете ја равенката: `3 sin x + 4 cos x = 2`.

Решение. Поделете ги двете страни на еднаквоста со `sqrt (3 ^ 2 + 4 ^ 2)`, добиваме:

`\ frac (3 sin x) (sqrt (3 ^ 2 + 4 ^ 2)) +` `\ frac (4 cos x) (sqrt (3 ^ 2 + 4 ^ 2)) = '' \ frac 2 (sqrt (3 ^ 2 + 4 ^ 2)) `

`3/5 грев x + 4/5 cos x = 2 / 5`.

Да означиме `3/5 = cos \ varphi`,` 4/5 = sin \ varphi`. Бидејќи `sin \ varphi> 0`,` cos \ varphi> 0`, тогаш земаме `\ varphi = arcsin 4 / 5` како помошен агол. Потоа ја запишуваме нашата еднаквост во форма:

`cos \ varphi sin x + sin \ varphi cos x = 2 / 5`

Применувајќи ја формулата за збир на агли за синус, ја запишуваме нашата еднаквост во следнава форма:

`грев (x + \ varphi) = 2 / 5`,

`x + \ varphi = (- 1) ^ n arcsin 2/5 + \ pi n`,` n \ во Z`,

`x = (- 1) ^ n arcsin 2/5-` `arcsin 4/5 + \ pi n`,` n \ во Z`.

Одговори. `x = (- 1) ^ n arcsin 2/5-` `arcsin 4/5 + \ pi n`,` n \ во Z`.

Дробно-рационални тригонометриски равенки

Тоа се равенства со дропки со тригонометриски функции во броителите и именителот.

Пример. Решете ја равенката. `\ frac (sin x) (1 + cos x) = 1-cos x`.

Решение. Помножете ја и поделете ја десната страна на еднаквоста со `(1 + cos x)`. Како резултат, добиваме:

`\ frac (sin x) (1 + cos x) = '' \ frac ((1-cos x) (1 + cos x)) (1 + cos x)`

`\ frac (sin x) (1 + cos x) =` `\ frac (1-cos ^ 2 x) (1 + cos x)`

`\ frac (sin x) (1 + cos x) =` `\ frac (sin ^ 2 x) (1 + cos x)`

`\ frac (sin x) (1 + cos x) -`` \ frac (sin ^ 2 x) (1 + cos x) = 0`

`\ frac (sin x-sin ^ 2 x) (1 + cos x) = 0`

Имајќи предвид дека именителот не може да биде еднаков на нула, добиваме `1 + cos x \ ne 0`,` cos x \ ne -1`, `x \ ne \ pi + 2 \ pi n, n \ во Z`.

Изедначете го броителот на дропката со нула: `sin x-sin ^ 2 x = 0`,` sin x (1-sin x) = 0`. Потоа `sin x = 0` или` 1-sin x = 0`.

1. `sin x = 0`,` x = \ pi n`, `n \ во Z`
2. `1-sin x = 0`,` sin x = -1`, `x = \ pi / 2 + 2 \ pi n, n \ во Z`.

Имајќи предвид дека `x \ ne \ pi + 2 \ pi n, n \ во Z`, решенијата се` x = 2 \ pi n, n \ во Z` и `x = \ pi / 2 + 2 \ pi n` , `n \ во Z`.

Одговори. `x = 2 \ pi n`,` n \ во Z`, `x = \ pi / 2 + 2 \ pi n`,` n \ во Z`.

Тригонометријата, а особено тригонометриските равенки, се користат во речиси сите области на геометријата, физиката, инженерството. Студијата започнува во 10 одделение, дефинитивно има задачи за испитот, затоа обидете се да ги запомните сите формули на тригонометриски равенки - тие дефинитивно ќе ви се најдат!

Сепак, дури и не треба да ги запаметите, главната работа е да ја разберете суштината и да можете да ги заклучите. Не е толку тешко како што звучи. Уверете се сами гледајќи го видеото.

Наједноставните тригонометриски равенки обично се решаваат со формули. Дозволете ми да ве потсетам дека следните тригонометриски равенки се нарекуваат наједноставни:

sinx = а

cosx = а

tgx = a

ctgx = a

x е аголот што треба да се најде,
а - кој било број.

А еве ги формулите со кои можете веднаш да ги запишете решенијата на овие наједноставни равенки.

За синус:

За косинус:

х = ± arccos a + 2π n, n ∈ Z

За тангента:

x = арктан a + π n, n ∈ Z

За котангента:

x = arcctg a + π n, n ∈ Z

Всушност, ова е теоретскиот дел од решавањето на наједноставните тригонометриски равенки. Згора на тоа, сè!) Воопшто ништо. Сепак, бројот на грешки на оваа тема е едноставно надвор од скалата. Особено ако примерот малку отстапува од шаблонот. Зошто?

Да, затоа што многу луѓе ги пишуваат овие букви, воопшто не разбирајќи го нивното значење!Со претпазливост тој запишува, без разлика како нешто се случува...) Ова мора да се реши. Тригонометрија за луѓето, или луѓето за тригонометрија на крајот на краиштата!?)

Ќе го сфатиме?

Еден агол ќе биде еднаков на arccos a, второ: -arccos a.

И секогаш така ќе функционира.За се а.

Ако не ми верувате, поставете го глувчето над сликата или допрете ја сликата на таблетот.) Го сменив бројот а до некои негативни. Како и да е, добивме еден агол arccos a, второ: -arccos a.

Затоа, одговорот секогаш може да се напише во форма на две серии корени:

x 1 = arccos a + 2π n, n ∈ Z

x 2 = - arccos a + 2π n, n ∈ Z

Ги комбинираме овие две серии во една:

x = ± arccos a + 2π n, n ∈ Z

И тоа е се. Добив општа формула за решавање на наједноставната тригонометриска равенка со косинус.

Ако разбирате дека ова не е некаква супернаучна мудрост, туку само скратена нотација на две серии одговори,вие и задачата „Ц“ ќе биде на рамо. Со неравенки, со избор на корени од даден интервал ... Таму одговорот со плус / минус не се тркала. И ако го третирате одговорот на деловен начин и го разделите на два одделни одговори, сè е решено.) Всушност, за ова разбираме. Што, како и каде.

Во наједноставната тригонометриска равенка

sinx = а

исто така се добиваат две серии на корени. Е секогаш. И овие две серии може да се снимаат една линија. Само оваа линија ќе биде полукава:

х = (-1) n arcsin a + π n, n ∈ Z

Но, суштината останува иста. Математичарите едноставно конструирале формула за да направат еден наместо два записи од низа корени. И тоа е тоа!

Ајде да ги провериме математичарите? И тогаш никогаш не се знае ...)

Во претходната лекција детално беше анализирано решението (без никакви формули) на тригонометриска равенка со синус:

Одговорот произведе две серии на корени:

x 1 = π / 6 + 2π n, n ∈ Z

x 2 = 5π / 6 + 2π n, n ∈ Z

Ако ја решиме истата равенка користејќи ја формулата, го добиваме одговорот:

x = (-1) n лаксин 0,5 + π n, n ∈ Z

Всушност, ова е недовршен одговор.) Ученикот мора да го знае тоа лаксин 0,5 = π / 6.Целосен одговор би бил:

x = (-1) n π / 6+ π n, n ∈ Z

Ова покренува интересно прашање. Одговори преку x 1; x 2 (тоа е вистинскиот одговор!) и преку осамените X (а ова е точниот одговор!) - истото, или не? Сега ќе дознаеме.)

Заменете како одговор со x 1 значење n = 0; еден; 2; и така натаму, сметаме, добиваме низа корени:

x 1 = π / 6; 13π / 6; 25π / 6 итн.

Со истата замена во одговорот со x 2 , добиваме:

x 2 = 5π / 6; 17π / 6; 29π / 6 итн.

Сега ги заменуваме вредностите n (0; 1; 2; 3; 4 ...) во општата формула за осамен X ... Односно, подигаме минус еден на нула, потоа на првиот, вториот, итн. И, се разбира, заменуваме 0 во вториот термин; еден; 2 3; 4, итн. И ние сметаме. Ја добиваме серијата:

x = π / 6; 5π / 6; 13π / 6; 17π / 6; 25π / 6 итн.

Тоа е сè што можете да видите.) Општата формула ни ја дава токму истите резултати,како двата одговора одделно. Само одеднаш, со ред. Немојте да бидете измамени од математичарите.)

Може да се проверат и формули за решавање на тригонометриски равенки со тангента и котангента. Но ние нема.) Тие се толку едноставни.

Целата оваа замена и проверка намерно ја опишав. Важно е да се разбере една едноставна работа овде: постојат формули за решавање на елементарни тригонометриски равенки, само краток запис од одговорите.За оваа краткост, морав да вметнам плус / минус во растворот на косинус и (-1) n во синусниот раствор.

Овие инсерти на никаков начин не се мешаат во задачите каде што треба само да го запишете одговорот на елементарната равенка. Но, ако треба да ја решите нееднаквоста, или тогаш треба да направите нешто со одговорот: изберете корени на интервал, проверете дали има ODZ, итн., овие инсерти лесно можат да ја вознемират личноста.

И што да се прави? Да, или запишете го одговорот во две серии или решете ја равенката/неравенката по тригонометрискиот круг. Тогаш овие инсерти исчезнуваат и животот станува полесен.)

Можеме да резимираме.

Постојат готови формули за одговор за решавање на наједноставните тригонометриски равенки. Четири парчиња. Тие се добри за моментално снимање на решението на равенката. На пример, треба да ги решите равенките:

sinx = 0,3

Лесно: х = (-1) n лаксин 0,3 + π n, n ∈ Z

cosx = 0,2

Нема проблем: х = ± arccos 0,2 + 2π n, n ∈ Z

tgx = 1,2

Лесно: x = арктан 1,2 + π n, n ∈ Z

ctgx = 3,7

Еден остана: x = arcctg3,7 + π n, n ∈ Z

cos x = 1,8

Ако вие, блескајќи со знаење, веднаш напишете го одговорот:

x = ± arccos 1,8 + 2π n, n ∈ Z

тогаш веќе блескаш, ова ... она ... од локва.) Точниот одговор: нема решенија. Дали разбирате зошто? Прочитајте што е аркозин. Дополнително, ако табеларните вредности на синус, косинус, тангента, котангента се на десната страна од првобитната равенка, - 1; 0; √3; 1/2; √3/2 итн. - одговорот низ сводовите ќе биде недовршен. Арките мора да се преведат во радијани.

И ако наидете на нееднаквост како

тогаш одговорот е:

х πn, n ∈ Z

има ретка глупост, да ...) Овде е неопходно да се одлучи за тригонометрискиот круг. Што ќе правиме во соодветната тема.

За оние кои херојски прочитале до овие редови. Едноставно не можам а да не ги ценам твоите титански напори. Ти бонус.)

Бонус:

Кога пишувате формули во алармантна борбена средина, дури и академски закоравените глупаци често се збунуваат околу тоа каде πn, И каде 2π n. Еве еден едноставен трик. Во од ситеформули вредни πn. Освен единствената формула со инверзен косинус. Таму стои 2πn. Двепиен. Клучен збор - два.Истата формула содржи двапотпише на почетокот. Плус и минус. Тука и таму - два.

Значи, ако сте напишале двазнак пред инверзниот косинус, полесно е да се запамети што ќе биде на крајот двапиен. Па дури и спротивното се случува. Прескокнете знак за човек ± , стигнува до крај, правилно пишува двапиен, и ќе си дојде при себе. Пред нешто двапотпишете! Личноста ќе се врати на почеток, но ќе ја исправи грешката! Како ова.)

Доколку ви се допаѓа оваа страница...

Патем, имам уште неколку интересни страници за вас.)

Можете да вежбате да решавате примери и да го дознаете вашето ниво. Тестирање за инстант валидација. Учење - со интерес!)

можете да се запознаете со функции и деривати.

Захарова Људмила Владимировна
МБОУ „Средно училиште бр.59“ во Барнаул
наставник по математика [заштитена е-пошта]

№1 Наједноставни тригонометриски равенки

Цел: 1. Изведете формули за решенија на наједноставните тригонометриски равенки на формата sinx = a, cosx = a, tgx = a, ctgx = a;

2. Научете да ги решавате наједноставните тригонометриски равенки користејќи формули.

Опрема: 1) Табели со графикони на тригонометриски функции y = sinx, y = cosx, y = tgx, y = ctgx; 2) Табела со вредности на инверзни тригонометриски функции; 3) Збирна табела на формули за решавање на наједноставните тригонометриски равенки.

План за лекција за предавање:

1 Изведување на формули за корените на равенката

а) синкс = а,

б) cosx = а,

в) tgx = а,

г) ctgx = а.

2 ... Усна фронтална работа за консолидирање на добиените формули.

3 ... Писмена работа за консолидирање на изучениот материјал

Во алгебра, геометрија, физика и други предмети, се соочуваме со најразлични проблеми, чиешто решение е поврзано со решавање на равенки. Ги проучувавме својствата на тригонометриските функции, па затоа е природно да се свртиме кон равенките во кои непознатата е содржана под знакот на функциите

Дефиниција: Равенки на формата синкс = а , cosx= а , tgx= а , ctgx= а се нарекуваат наједноставни тригонометриски равенки.

Многу е важно да научите како да ги решавате наједноставните тригонометриски равенки, бидејќи сите методи и техники за решавање на какви било тригонометриски равенки треба да ги сведете на наједноставните.

Да почнеме со изведување формули кои „активно“ работат при решавање на тригонометриски равенки.

1.Равенки од формата sinx = а.

Да ја решиме равенката sinx = аграфички. За да го направите ова, во еден координатен систем, ги исцртуваме графиконите на функциите y = sinx и y = а.

1) Ако а> 1 и агрев x = анема решенија, бидејќи правата линија и синусоидот немаат заеднички точки.

2) Ако -1a a го премине синусоидот бесконечно многу пати. Ова значи дека равенкатасинкс = аима бесконечно многу решенија.

Бидејќи периодот на синус е 2 , потоа да се реши равенкатасинкс = адоволно е да се најдат сите решенија на кој било сегмент со должина 2.

Со решавање на равенката за [- / 2; / 2] според дефиницијата на лак-син x =лаксин а, и на x = -arcsin а... Земајќи ја предвид периодичноста на функцијата y = sinx, ги добиваме следните изрази

x = -арцин а+ 2n, n Z.

Двете серии на решенија може да се комбинираат

X = (-1) n лаксин а+ n, nZ.

Во следните три случаи, тие претпочитаат да ја користат не општата формула, туку поедноставните односи:

Ако а= -1, потоа sin x = -1, x = - / 2 + 2n

Ако а= 1, потоа sin x = 1, x = / 2 + 2n

Ако a = 0, потоа sin x = 0. x = n,

Пример: Реши равенка sinx = 1/2.

Да ги составиме формулите за решенијата x = arcsin 1/2 + 2n

X = - arcsin a + 2n

Ајде да ја пресметаме вредноста arcsin1/2. Заменете ја пронајдената вредност во формулите за решение

x = 5/6 + 2 n

или според општата формула

X = (-1) n лаксин 1/2 + n,

X = (-1) n / 6 + n,

2. Равенки на формата cosx = а.

Да ја решиме равенката cosx = аисто така и графички, исцртувајќи ги графиконите на функциите y = cosx и y = а.

1) Ако a 1, тогаш равенката cosx = анема решенија, бидејќи графиконите немаат заеднички точки.

2) Ако -1 а cosx = аима бесконечен број решенија.

Ќе ги најдеме сите решенија cosx = ана интервал од должина 2 бидејќи периодот на косинус е 2.

На решението на равенката по дефиниција на аркозинот ќе биде x =аркос а. Со оглед на парноста на косинусната функција, решението на равенката на [-; 0] ќе биде x = -arcos а.

Така, решенијата на равенката cosx = а x = + аркос а+ 2 n,

Во три случаи, ќе користиме не општа формула, туку поедноставни односи:

Ако а= -1, потоа cosx = -1, x = - / 2 + 2n

Ако а= 1, потоа cosx = 1, x = 2n,

Ако a = 0, тогаш cosx = 0. x = / 2 + n

Пример: Реши равенка cos x = 1/2,

Да ги составиме формулите за решенијата x = arccos 1/2 + 2n

Ајде да ја пресметаме вредноста arccos1/2.

Заменете ја пронајдената вредност во формулите за решение

X = + /3+ 2n, nZ.

Равенки на формата tgx = а.

Бидејќи периодот на тангентата е еднаков, тогаш за да се најдат сите решенија на равенката tgx = а, доволно е да се најдат сите решенија на кој било интервал од должина. Според дефиницијата на арктангенсот, решението на равенката на (- / 2; / 2) е арктан а. Земајќи го предвид периодот на функцијата, сите решенија на равенката можат да се напишат во форма

x = arctg а+ n, nZ.

Пример:Решете ја равенката tg x = 3/3

Ајде да составиме формула за решавање на x =арктан 3/3 + n, nZ.

Ја пресметуваме вредноста на арктангенсотарктан 3/3 = / 6, тогаш

X = / 6 + n, nZ.

Изведување формула за решавање на равенка Со tgx= аможе да им се обезбеди на студентите.

Пример.

Решете ја равенката ctg x = 1.

x = arcсtg 1 + n, nZ,

X = / 4 + n, nZ.

Како резултат на изучениот материјал, студентите можат да ја пополнат табелата:

„Решавање тригонометриски равенки“.

равенката

Вежби за консолидирање на изучениот материјал.

(Усно) Која од напишаните равенки може да се реши со формулите:

а) x = (-1) n лаксин а+ n, nZ;

б) x = + аркос а + 2 n?

cos x = 2/2, tg x = 1, sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 ...

Кои од наведените равенки немаат решенија?

Решете ги равенките:

а) sin x = 0; д) sin x = 2/2; ж) sin x = 2;

б) cos x = 2/2; ѓ) cos x = -1/2; з) cos x = 1;

г) tg x = 3; е) ctg x = -1; ѕ) tg x = 1/3.

3. Реши ги равенките:

а) грев 3x = 0; д) 2cos x = 1;

б) cos x / 2 = 1/2; ѓ) 3 тен 3x = 1;

г) грев x / 4 = 1; е) 2cos (2x + / 5) = 3.

При решавање на овие равенки, корисно е да се запишат правилата за решавање на равенките на форматагрев v x = а, и Согрев v x = а, | а|1.

Грев v x = a, | a | 1.

v x = (-1) n лаксин а+ n, nZ,

x = (-1) n 1 / vлаксин а+ n / v, nZ.

Сумирајќи ги резултатите од лекцијата:

Денес во лекцијата изведовме формули за решавање на наједноставните тригонометриски равенки.

Демонтирани примери за решавање на наједноставните тригонометриски равенки.

Ја пополнивме табелата со која ќе ги решиме равенките.

Домашна работа.

№2 Решавање тригонометриски равенки

Цел: Да се ​​изучуваат методите за решавање на тригонометриски равенки: 1) редуцирани до квадратни, 2) сведени на хомогени тригонометриски равенки.

Да се ​​развијат вештините за набљудување кај учениците при користење на различни методи за решавање на тригонометриски равенки.

Фронтална работа со ученици.

Кои се формулите за корените на тригонометриските равенки cos x = а, грев x = а, tgx = а, ctg x = а.

Решете ги равенките (усно):

cos x = -1, sin x = 0, tgx = 0, ctg x = 1, cos x = 1,5, sin x = 0.

Најдете грешки и размислете за причините за грешките.

cos x = 1/2, x = + / 6 + 2к, к З.

sin x = 3/2, x = / 3 + k, kZ.

tgx = / 4, x = 1 + k, kZ.

2. Учење на нов материјал.

Оваа лекција ќе опфати некои од најчестите методи за решавање на тригонометриски равенки.

Тригонометриски равенки сведени на квадратни.

Оваа класа може да вклучува равенки кои вклучуваат една функција (синус или косинус) или две функции од еден аргумент, но едната од нив се сведува на втората со помош на основни тригонометриски идентитети.

На пример, ако cosх е вклучена во равенката во парни сили, тогаш го заменуваме со 1- sin 2 x, ако sin 2 x, тогаш го заменуваме со 1-cos 2 x.

Пример.

Решете ја равенката: 8грев 2 x - 6sin x -5 = 0.

Решение: Означуваме sin x = t, потоа 8t 2 - 6t - 5 = 0,

D = 196,

Т 1 = -1/2, т 2 = -5/4.

Да ја извршиме обратната промена и да ги решиме следните равенки.

X = (- 1) k + 1/6 + k, kZ.

Од -5/4> 1, равенката нема корени.

Одговор: x = (- 1) k + 1/6 + k, kZ.

Решение на вежби за зајакнување.

Реши ја равенката:

1) 2sin 2 x + 3cos x = 0;

2) 5sin 2 x + 6cos x -6 = 0;

3) 2sin 2 x + 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1 = 0.

Хомогени тригонометриски равенки.

Дефиниција: 1) Равенка на форматаа синкс + б cosx= 0, (a = 0, b = 0)се нарекува хомогена равенка од прв степен во однос на sin x и cos x.

Оваа равенка се решава со делење на двата нејзини дела со cosx 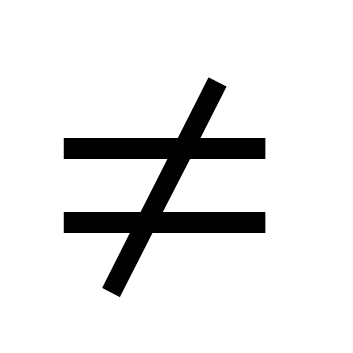0. Резултатот е равенката atgx + b = 0.

2) Равенка на форматаа грев 2 x + б синкс cosx + в cos 2 x =0 се нарекува хомогена равенка од втор степен, каде што a, b, c се сите броеви.

Ако a = 0, тогаш равенката се решава со делење на двата дела со cos 2 x 0. Како резултат на тоа, ја добиваме равенката atg 2 x + btgx + c = 0.

Коментар:Равенка на форматаа грев mx + б cos mx=0 или

а грев 2 mx + б грев mx cos mx + в cos 2 mx =0 се исто така хомогени. За да се решат, двете страни на равенката се делат со cos mx=0 или cos 2 mx=0

3) Различни равенки може да се сведат на хомогени равенки, кои првично не се такви. На пример,грев 2 mx + б грев mx cos mx + в cos 2 mx = г, и а синкс + б cosx= г. За да ги решите овие равенки, треба да ја помножите десната страна со „Тригонометриска единица“тие. на грев 2 x + cos 2 xи вршат математички трансформации.

Вежби за консолидирање на изучениот материјал:

1) 2sin x- 3cos x = 0; 5) 4 грев 2 x - sin2x = 3;

2) грев 2x + cos2x = 0; 6) 3 sin 2 x + sinx cosx = 2 cos 2 x;

3) sin x + 3cos x = 0; 7) 3 грев 2 x- sinx cosx = 2;

4) sin 2 x -3 sinx cosx +2 cos 2 x = 0

3. Сумирање на резултатите од лекцијата. Домашна работа.

Во оваа лекција, во зависност од подготвеноста на групата, можете да размислите за решавање на равенките на формата a sin mx + b cos mx = c, каде што a, b, c не се еднакви на нула во исто време.

Вежби за зајакнување:

1.3sin x + cos x = 2;

2.3sin 2x + cos 2x = 2;

3.sin x / 3 + cos x / 3 = 1;

4.12 sin x +5 cos x + 13 = 0.

№ 3 Решавање тригонометриски равенки

Цел: 1) Проучување на методот на решавање на тригонометриски равенки со факторизација; да научи да решава тригонометриски равенки користејќи различни тригонометриски формули;

2) Проверете: знаењето на учениците за формули за решавање на наједноставните тригонометриски равенки; способност за решавање на наједноставните тригонометриски равенки.

План за лекција:

Проверка на домашната задача.

Математички диктат.

Учење нов материјал.

Самостојна работа.

Сумирајќи ги резултатите од лекцијата. Домашна работа.

Тек на лекцијата:

Проверка на домашната задача (решението на тригонометриските равенки е накратко запишано на таблата).

Математички диктат.

ВО 1

1. Кои равенки се нарекуваат наједноставни тригонометриски равенки?

2. Како се вика равенката на форматаа sinx + б cosx = 0? Ве молиме посочете го начинот на решавање.

3. Напиши ја формулата за корените на равенката tgx = а(ctg x = а).

4. Запиши ги формулите за корените на равенките на формата cosx = а, каде а=1, а=0, а=-1.

5. Запишете ја општата формула за корените на равенкатагрев x = а, | а|

6. Како се равенките на форматаа cosx = б, | б|

ВО 2

1. Запишете ги формулите за корените на равенките cosx = а,| а|

2. Запишете ја општата формула за корените на равенката

= а, | а|

3. Како се нарекуваат равенките на форматагрев x = а, tgx = а, грев x = а?

4. Запишете ги формулите за корените на равенкатагрев x = а, ако а=1, а=0, а=-1.

5.Како се равенките на форматагрев а x = б, | б|

6. Кои равенки се нарекуваат хомогени равенки од втор степен? Како се решаваат?

Учење нов материјал.

Метод на факторинг.

Еден од најчесто користените методи за решавање на тригонометриски равенки е методот на факторизација.

Ако равенката f (x) = 0 може да се претстави како f 1 (x) f 2 (x) = 0, тогаш проблемот се сведува на решавање на две равенки f 1 (x) = 0, f 2 (x) = 0 .

(Кај учениците, корисно е да се запамети правилото „ Производот на факторите е нула ако барем еден од факторите е нула, додека другите имаат смисла»)

Консолидација на изучениот материјал преку решавање на равенки со различна сложеност.

(грев x-1/2) (грев x + 1) = 0; 2) (cosx- 2/2) (грев x + 2/2) = 0; (само)

3) грев 2 x + грев x cosx = 0; 4) грев 2 x - грев x = 0;

5) грев 2x - cosx = 0; 6) 4 cos 2 x -1 = 0; (На 2 начини)

7) cosx + cos3x = 0; 8) грев 3х = грев 17х;

9) грев x + грев 2x + грев 3x = 0; 10) cos3x cos5x

11) грев x cos5x = грев 9x cos3x грев 2x грев 2x

12) 3 cosx sin x + cos 2 x = 0 (само)

13) 2 cos 2 x - грев (x- / 2) + tgx tg (x + / 2) = 0.

Самостојна работа.

Опција-1 Опција-2

1) 6 sin 2 x + 5sin x -1 = 0; 1) 3 cos 2 x + 2 cosx -5 = 0;

2) грев 2x - cos2x = 0; 2) 3 cos x / 2 - грев x / 2 = 0;

3) 5 sin 2 x + sin x cosx -2 cos 2 x = 2; 3) 4sin 2 x- sin x cosx + 7cos 2 x = 5;

4) sin x + sin5x = sin3x + sin7x; 4) грев х-грев 2х + грев 3х-грев 4х = 0;

5) sin x + cosx = 1. 5) sin x + cosx = 2.

8. Сумирање на лекцијата. Домашна работа.