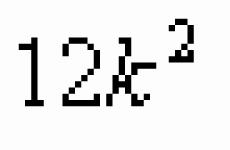Methods for proving identities. Identity. Methods for proving identities What does it mean to prove an identity example

What is identity? And how to prove it? and got the best answer

Answer from Yovetlan Bezrukikh [active]

Methods for proving identity:

So, we transform:

-36=-36.
Identity is proven!

Answer from Џna Kichak[active]
You clever! Do you know what identity is? Grade 7 algebra. Identity-statement requiring proof. And it's easy to prove, to simplify.

Answer from Ўliya Frolova[guru]
Identity - equality that holds for any values of the variable.
x squared + 8x-5x-40's squared + x - 4x + 4 = - 36
-36=-36

Answer from Andrey Shadrov[newbie]
Identity is an equation that is satisfied identically, that is, it is valid for any admissible values of the variables included in it. To prove an identity means to establish that for all admissible values of the variables its left and right sides are equal.
Methods for proving identity:
1. Perform transformations on the left side and get the right side as a result.
2. Perform transformations on the right side and finally get the left side.
3. Separately transform the right and left parts and get the same expression in the first and second cases.
4. Make up the difference between the left and right sides and get zero as a result of its transformations.
Since we cannot transform the right side, therefore, we will transform the left. (Since I cannot write a number raised to the second power, for example, the number-x squared, I will write like this: x multiplied by x, abbreviated x multiplied by x)
So, we transform:
x smart. on x + 8x - 5x - 40 - x smart. on x + x - 4x + 4 = -36,
(We can mutually destroy many numbers! These are x in square degrees, because one of them is positive, the other negative, and similar numbers - 8x; -5x; x; -4x. Because 8x - 5x + x - 4x = 0) ...
As a result, we got -40 + 4 = -36.
By doing a simple math operation 4-40, we get -36.
-36=-36.
Identity is proven!

Answer from Alexander Chernyshov[newbie]
aaaaa

Proof of identities. There are many concepts in mathematics. One of them is identity.

An identity is an equality that holds for all values of the variables that are included in it.

We already know some of the identities. For example, all abbreviated multiplication formulas are identities.

Prove identity- this means to establish that for any admissible value of the variable its left side is equal to the right side.

In algebra, there are several different ways to prove identities.

Methods for proving identities

left side of the identity. If in the end we get the right-hand side, then the identity is considered proven.
Perform equivalent transformations the right side of the identity. If in the end we get the left-hand side, then the identity is considered proven.
Perform equivalent transformations left and right sides of the identity. If, as a result, we get the same result, then the identity is considered proven.
Subtract the left side from the right side of the identity.
The right side is subtracted from the left side of the identity. We perform equivalent transformations on the difference. And if in the end we get zero, then the identity is considered proven.

It should also be remembered that the identity is valid only for the admissible values of the variables.

As you can see, there are a lot of ways. Which method to choose in this particular case depends on the identity that you need to prove. As you prove different identities, experience will come in choosing a method of proof.

Let's look at some simple examples

Example 1.

Prove the identity x * (a + b) + a * (b-x) = b * (a + x).

Solution.

Since there is a small expression on the right side, let's try to transform the left side of the equality.

We have,

x * (a + b) + a * (b-x) = x * a + x * b + a * b - a * x.

We present similar terms and take the common factor out of the bracket.

x * a + x * b + a * b - a * x = x * b + a * b = b * (a + x).

We got that the left side after the transformations became the same as the right side. Therefore, this equality is an identity.

Example 2.

Prove the identity a ^ 2 + 7 * a + 10 = (a + 5) * (a + 2).

Solution.

In this example, you can proceed in the following way. Let's expand the brackets on the right-hand side of the equality.

We get

(a + 5) * (a + 2) = (a ^ 2) + 5 * a + 2 * a + 10 = a ^ 2 + 7 * a + 10.

We see that after the transformations, the right side of the equality became the same as the left side of the equality. Therefore, this equality is an identity.

Learning goal:

repeat the definitions of the equation, identity;

learn to distinguish between the concepts of equation and identity;

identify ways of proving identities;

repeat the methods of reducing a monomial to the standard form, adding polynomials, multiplying a monomial by a polynomial when proving identities.

Developing goal:

develop literate mathematical speech of students (enrich and complicate vocabulary when using special mathematical terms),

develop thinking: the ability to compare, analyze, draw analogies, predict, draw conclusions (when choosing methods of proving identities);

develop the educational and cognitive competence of students.

Educational purpose:

develop the ability to work in a group, coordinate their activities with other participants in the educational process;

foster tolerance.

Lesson type: complex application of knowledge.

Lesson steps: preparatory, application of knowledge, result.

The border of knowledge - ignorance:

can apply operations of converting a monomial to a standard form;

addition of polynomials, multiplication of a polynomial by a polynomial.

Distinguish between the concepts of equation and identity;

carry out the proof of identities;

rationally choose and apply methods of proving identities.

Frontal work

Verbal

Visual

Application of knowledge (ensuring the assimilation of new knowledge and methods of action at the level of application in a changed educational situation)

Based on the transformations of the left and right sides of this

mathematical equality, identify ways of proving identities;

Reveal a rational way from the proposed ones and work out the selection of a rational solution for a given condition of identities

Group work

Independent work

Practical

Outcome (analysis and assessment of the success of achieving the goal)

Summing up the work in the lesson by performing individual work, where it is proposed to choose an identity from the presented equalities and prove it in any of the proposed ways (preferably rational);

Then students make a self-assessment of their work in the lesson according to the specified (from the beginning of the lesson) criteria

Frontal

Verbal

Lesson summary (briefly):

1. Stage (preparatory)

Consider the math notation: (frontal work)

Grade 7 students, as a rule, believe that this is an equation, and, solving it, they get a linear equation of the form: 0 x = 0, valid for any x.

Then, the teacher shows the work of another class, and the children are faced with a contradiction - in the work of another class, the students prove that this is an identity.

Conclusion: attention should be paid to the fact that one and the same equality can be regarded as an identity and as an equation. It depends on the condition for the given work: if it is required to establish at what value of the variable equality takes place, then this- the equation. And if it is required to prove that equality holds for any values of the variables -identity.

2. Stage (application)

Revealing ways to prove identities: (group work)

The expression is written:

Practical task in groups to identify ways of proving identities:

Observe the rules for working in groups (they are printed on the plates displayed by the teacher at the students' workplaces)

On a Whatman paper, in a joint work, perform some transformations according to a certain technology indicated in the assignment to the group and prove that the given expression does not depend on the values of the variables, which means it is an identity;

Give an explanation of the work done and make a conclusion: what is the given method of proving identities;

Task for group 1:

Move the right side of the equality to the left. Prove that the given expression does not depend on the value of the variables.

Task for group 2:

Convert the left side of equality. Prove that it is equal to the right one, which means that this expression does not depend on the values of the variables.

Task for group 3:

Convert the left and right sides of equality at the same time. Prove that this equality does not depend on the value of the variables.

When considering the work done by the guys to prove the identity, it is convenient to depict the results of the applied methods in the form of diagrams on separate sheets of paper, with a number indicator, so that later, to use these diagrams not only in this one, but also in other algebra lessons.

3. Stage (summary)

a) Identities for choosing a rational solution: (frontal work)

LECTURE №3 Proof of identities

Objective: 1. Review the definitions of identity and identically equal expressions.

2. Introduce the concept of identical transformation of expressions.

3. Multiplication of a polynomial by a polynomial.

4. Decomposition of a polynomial into factors by the grouping method.

May every day and every hour

We will get something new,

May our mind be kind,

And the heart will be smart!

There are many concepts in mathematics. One of them is identity.

An identity is an equality that holds for all values of the variables that are included in it. We already know some of the identities.

For example, all abbreviated multiplication formulas are identities.

Abbreviated multiplication formulas

1. (a ± b)2 = a 2 ± 2 ab + b 2,

2. (a ± b)3 = a 3 ± 3 a 2b + 3ab 2 ± b 3,

3. a 2 - b 2 = (a - b)(a + b),

4. a 3 ± b 3 = (a ± b)(a 2 ab + b 2).

Prove identity- this means to establish that for any admissible value of the variable its left side is equal to the right side.

In algebra, there are several different ways to prove identities.

Methods for proving identities

left side of the identity.

the right side of the identity.

left and right sides of the identity.

Subtract the left side from the right side of the identity.

The right side is subtracted from the left side of the identity.

It should also be remembered that the identity is valid only for the admissible values of the variables.

Identity is an equation that is satisfied identically, that is, it is valid for any admissible values of the variables included in it. To prove an identity means to establish that for all admissible values of the variables, its left and right sides are equal.
Methods of proving identity:
1. Perform transformations on the left side and get the right side as a result.
2. Perform transformations on the right side and finally get the left side.
3. Separately transform the right and left parts and get the same expression in the first and second cases.
4. Make up the difference between the left and right sides and get zero as a result of its transformations.
Let's look at some simple examples

Example 1. Prove the identity x (a + b) + a (b-x) = b (a + x).

Solution.

Since there is a small expression on the right side, let's try to transform the left side of the equality.

x (a + b) + a (b-x) = x a + x b + a b - a x.

We present similar terms and take the common factor out of the bracket.

x a + x b + a b - a x = x b + a b = b (a + x).

We got that the left side after the transformations became the same as the right side. Therefore, this equality is an identity.

Example 2. Prove the identity: a² + 7a + 10 = (a+5) (a+2).

Solution:

In this example, you can proceed in the following way. Let's expand the brackets on the right-hand side of the equality.

(a + 5) (a + 2) = (a²) + 5 a + 2 a +10 = a² + 7 a + 10.

We see that after the transformations, the right side of the equality became the same as the left side of the equality. Therefore, this equality is an identity.

"The replacement of one expression with another, identically equal to it, is called the identical transformation of the expression"

Find out which equality is an identity:

1. - (a - b) = - a - b;

2. 2 (x + 4) = 2x - 4;

3. (x - 5) (-3) = - 3x + 15.

4. pxy (- p2 x2 y) = - p3 x3 y3.

"To prove that some equality is an identity, or, as they say otherwise, to prove identity, use identical transformations of expressions"

The equality is true for any values of the variables, called identity. To prove that some equality is an identity, or, as they say otherwise, to prove identity, use identical transformations of expressions.
Let us prove the identity:
xy - 3y - 5x + 16 = (x - 3) (y - 5) + 1 Rewrite the left side of this equality:
xy - 3y - 5x + 16 = (xy - 3y) + (- 5x + 15) +1 = y (x - 3) - 5 (x -3) +1 = (y - 5) (x - 3) + 1 As a result identity transformation left-hand side of the polynomial, we obtained its right-hand side and thereby proved that this equality is identity.
For proof of identity transform its left side to the right or its right side to the left, or show that the left and right sides of the original equality are identically equal to the same expression.

Multiplying a polynomial by a polynomial

Multiply the polynomial a + b by polynomial c + d... Let's compose the product of these polynomials:
(a + b) (c + d).
We denote the binomial a + b letter x and transform the resulting product according to the rule of multiplication of a monomial by a polynomial:
(a + b) (c + d) = x (c + d) = xc + xd.
Into expression xc + xd. substitute for x polynomial a + b and again use the rule of multiplying a monomial by a polynomial:
xc + xd = (a + b) c + (a + b) d = ac + bc + ad + bd.
So: (a + b) (c + d) = ac + bc + ad + bd.
Product of polynomials a + b and c + d we have presented as a polynomial ac + bc + ad + bd... This polynomial is the sum of all monomials obtained by multiplying each term of the polynomial a + b for each term of the polynomial c + d.
Conclusion: the product of any two polynomials can be represented as a polynomial.
The rule: to multiply a polynomial by a polynomial, you need to multiply each term of one polynomial by each term of the other polynomial and add the resulting products.
Note that when multiplying a polynomial containing m terms by a polynomial containing n members in the work before bringing similar members should turn out mn members. This can be used for control.

Decomposition of a polynomial into factors by the grouping method:

Earlier, we got acquainted with factoring a polynomial by factoring out the common factor outside the parentheses. Sometimes it is possible to factor out a polynomial using another way - grouping of its members.
Factor the polynomial
ab - 2b + 3a - 6 Group it so that the terms in each group have a common factor and factor this factor out of the parentheses:
ab - 2b + 3a - 6 = (ab - 2b) + (3a - 6) = b (a - 2) + 3 (a - 2) Each term in the resulting expression has a common factor (a - 2). Let's take this common factor out of the parentheses:
b (a - 2) + 3 (a - 2) = (b +3) (a - 2) As a result, we factorized the original polynomial:
ab - 2b + 3a - 6 = (b +3) (a - 2) The way we used to factorize a polynomial is called way of grouping.
Polynomial decomposition ab - 2b + 3a - 6 multipliers can be done by grouping its members differently:
ab - 2b + 3a - 6 = (ab + 3a) + (- 2b - 6) = a (b + 3) -2 (b + 3) = (a - 2) (b + 3)

Repeat:

1. Methods for proving identities.

2. What is called the identity transformation of an expression.

3. Multiplication of a polynomial by a polynomial.

4. Factoring a polynomial by the grouping method