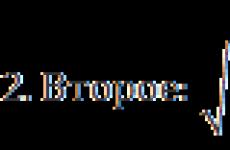त्रिकोणमितीय सर्कल पर कोनों की गिनती। सकारात्मक और नकारात्मक कोण। तिमाहियों में कोनों का वितरण। कोने माप नकारात्मक नकारात्मक हो सकता है
कोण: ° π रेड \u003d
में कनवर्ट करें: रेडियंस डिग्री 0 - 360 डिग्री 0 - 2π सकारात्मक नकारात्मक गणना
जब प्रत्यक्ष छेड़छाड़ होती है, तो चौराहे बिंदु के सापेक्ष चार अलग-अलग क्षेत्रों को प्राप्त किया जाता है।
इन नए क्षेत्रों को बुलाया जाता है कोने.
तस्वीर डायरेक्ट एबी और सीडी के चौराहे द्वारा बनाई गई 4 अलग-अलग कोण दिखाती है
आम तौर पर, कोणों को डिग्री में मापा जाता है, जो ° के रूप में संकेत दिया जाता है। जब ऑब्जेक्ट एक पूर्ण सर्कल करता है, यानी, बी, सी, ए, और फिर डी के माध्यम से बिंदु डी से आगे बढ़ रहा है, तो वे कहते हैं कि यह 360 डिग्री (360 डिग्री) हो गया। इस प्रकार, डिग्री $ \\ frac (1) (360) $ सर्कल है।
कोण 360 से अधिक डिग्री
हमने इस बारे में बात की कि ऑब्जेक्ट बिंदु के चारों ओर एक पूर्ण सर्कल बनाता है, फिर यह 360 डिग्री पास करता है, हालांकि, जब ऑब्जेक्ट एक से अधिक सर्कल बनाता है, तो यह 360 डिग्री से अधिक का कोण बनाता है। यह रोजमर्रा की जिंदगी में एक आम घटना है। पहिया कई मंडलियों को गुजरता है जब कार चलती है, यानी, यह 360 डिग्री से अधिक कोण बनाती है।
ऑब्जेक्ट घुमाए जाने पर चक्रों की संख्या (सर्कल कवर) की संख्या का पता लगाने के लिए, हम इस कोण से बराबर या उससे छोटे होने के लिए 360 को जोड़ने के लिए आवश्यक समय की संख्या पर विचार करते हैं। इसी तरह, हमें लगता है कि हम संख्या 360 पर कई छोटे प्राप्त करने के लिए गुणा करते हैं, लेकिन इस कोने के सबसे नज़दीक हैं।
उदाहरण 2।
1. कोण द्वारा वर्णित मंडलियों की संख्या का पता लगाएं
a) 380 °
b) 770 °
ग) 1000 डिग्री
फेसला
a) 380 \u003d (1 × 360) + 20
वस्तु ने एक सर्कल और 20 ° का वर्णन किया
$ 20 ^ (\\ curch) \u003d \\ frac (20) (360) \u003d \\ frac (1) (18) $ सर्कल
ऑब्जेक्ट ने $ 1 \\ frac (1) (18) $ मंडल वर्णित किया।
बी) 2 × 360 \u003d 720
770 \u003d (2 × 360) + 50
वस्तु ने दो मंडलियों और 50 ° का वर्णन किया
$ 50 ^ (\\ सर्क) \u003d \\ frac (50) (360) \u003d \\ frac (5) (36) $ सर्कल
ऑब्जेक्ट ने $ 2 \\ frac (5) (36) $ सर्कल का वर्णन किया
सी) 2 × 360 \u003d 720
1000 \u003d (2 × 360) + 280
$ 280 ^ (\\ circ) \u003d \\ frac (260) (360) \u003d \\ frac (7) (9) $ घेरे
ऑब्जेक्ट ने $ 2 \\ frac (7) (9) $ मंडल वर्णित किया
जब ऑब्जेक्ट घड़ी की दिशा में घूमता है, तो यह रोटेशन का नकारात्मक कोण बनाता है, और जब यह वामावर्त घुमाता है - एक सकारात्मक कोण। इस बिंदु तक, हम केवल सकारात्मक कोण माना जाता है।
एक आरेख के रूप में, एक नकारात्मक कोण को नीचे दिखाए गए अनुसार चित्रित किया जा सकता है। 
नीचे दिया गया आंकड़ा कोण का संकेत दिखाता है, जिसे कुल रेखा, 0 अक्ष (अनुपस्थित धुरी अक्ष) से \u200b\u200bमापा जाता है 
इसका मतलब है कि एक नकारात्मक कोण की उपस्थिति में, हम इसी सकारात्मक कोण प्राप्त कर सकते हैं।
उदाहरण के लिए, लंबवत प्रत्यक्ष का निचला हिस्सा 270 डिग्री है। जब एक नकारात्मक दिशा में मापा जाता है, तो हमें -90 डिग्री मिलते हैं। हम बस 360 में से 270 घटाएं। एक नकारात्मक कोण होने के बाद, हम एक सकारात्मक कोण प्राप्त करने के लिए 360 जोड़ते हैं।
जब एक कोण -360 डिग्री होता है, तो इसका मतलब है कि वस्तु ने एक से अधिक सर्कल घड़ी की दिशा में किया है।
उदाहरण 3।
1. उपयुक्त सकारात्मक कोण का पता लगाएं
a) -35 °
b) -60 °
C) -180 °
डी) - 670 डिग्री
2. 80 डिग्री, 167 डिग्री, 330 डिग्री और 1300 डिग्री के इसी नकारात्मक कोण को ढूंढें।
फेसला
1. उचित सकारात्मक कोण खोजने के लिए, हम 360 कोने मूल्य में जोड़ते हैं।
ए) -35 डिग्री \u003d 360 + (-35) \u003d 360 - 35 \u003d 325 डिग्री
b) -60 ° \u003d 360 + (-60) \u003d 360 - 60 \u003d 300 °
सी) -180 डिग्री \u003d 360 + (-180) \u003d 360 - 180 \u003d 180 डिग्री
डी) -670 डिग्री \u003d 360 + (-670) \u003d -310
इसका मतलब है एक सर्कल दक्षिणावर्त (360)
360 + (-10) \u003d 50 °
कोण 360 + 50 \u003d 410 ° है
2. उचित नकारात्मक कोण प्राप्त करने के लिए, हम कोण मूल्य से 360 घटाते हैं।
80 डिग्री \u003d 80 - 360 \u003d - 280 डिग्री
167 ° \u003d 167 - 360 \u003d -193 °
330 डिग्री \u003d 330 - 360 \u003d -30 डिग्री
1300 ° \u003d 1300 - 360 \u003d 940 (एक सर्कल पास)
940 - 360 \u003d 580 (दूसरा दौर उत्तीर्ण)
580 - 360 \u003d 220 (तीसरा सर्कल पारित)
220 - 360 \u003d -140 °
कोण -360 - 360 - 360 - 140 \u003d -1220 °
इस प्रकार, 1300 ° \u003d -1220 °
कांति
रेडिन सर्कल के केंद्र का कोण है, जिसमें चाप निष्कर्ष निकाला जाता है, जिसकी लंबाई इस सर्कल के त्रिज्या के बराबर होती है। यह एक कोणीय मान के माप की एक इकाई है। ऐसा कोण लगभग 57.3 डिग्री है।
ज्यादातर मामलों में, यह संकेत दिया जाता है प्रसन्न.
इस प्रकार $ 1 rad \\ apprount 57.3 ^ (\\ सर्क) $ 
त्रिज्या \u003d आर \u003d ओए \u003d ओबी \u003d एबी
बोआ कोण एक राडिया के बराबर है
चूंकि परिधि की लंबाई $ 2 \\ पीआई आर $ के रूप में सेट की जाती है, फिर $ 2 \\ पीआई $ रेडी की परिधि में, जिसका अर्थ है सामान्य रूप से सर्कल $ 2 \\ PI $ रेडियन।
गणना में दशमलव भागों से बचने के लिए रेडियंस आमतौर पर $ \\ PI $ द्वारा व्यक्त किए जाते हैं। ज्यादातर पुस्तकों में, संक्षिप्त नाम रेड (रेड) नहीं मिला, लेकिन पाठक को पता होना चाहिए कि जब इसे कोण की बात आती है, तो यह $ \\ PI $ के माध्यम से सेट किया जाता है, और माप की इकाइयां स्वचालित रूप से रेडियंस बन जाती हैं।
$ 360 ^ (\\ सर्क) \u003d 2 \\ Pi \\ RAD $
$ 180 ^ (\\ सर्क) \u003d \\ PI \\ RAD $
$ 90 ^ (\\ सर्क) \u003d \\ frac (\\ pi) (2) RAD $
$ 30 ^ (\\ curch) \u003d \\ frac (30) (180) \\ pi \u003d \\ frac (\\ pi) (6) RAD $
$ 45 ^ (\\ cirp) \u003d \\ frac (45) (180) \\ pi \u003d \\ frac (\\ pi) (4) RAD $
$ 60 ^ (\\ सर्क) \u003d \\ frac (60) (180) \\ pi \u003d \\ frac (\\ pi) (3) RAD $
$ 270 ^ (\\ circ) \u003d \\ frac (270) (180) \\ pi \u003d \\ frac (27) (18) \\ pi \u003d 1 \\ frac (1) (2) \\ pi \\ rad $
उदाहरण 4।
1. $ \\ PI $ के माध्यम से 240 डिग्री, 45 डिग्री, 270 डिग्री, 750 डिग्री और 3 9 0 डिग्री रेडियंस में कनवर्ट करें।
फेसला
मैं $ \\ FRAC (\\ PI) (180) $ पर कोनों को गुणा करता हूं।
$ 240 ^ (\\ सर्क) \u003d 240 \\ Times \\ Frac (\\ PI) (180) \u003d \\ frac (4) (3) \\ pi \u003d 1 \\ frac (1) (3) \\ pi $
$ 120 ^ (\\ सर्क) \u003d 120 \\ Times \\ Frac (\\ PI) (180) \u003d \\ frac (2 \\ pi) (3) $
$ 270 ^ (\\ सर्क) \u003d 270 \\ Tales \\ Frac (1) (180) \\ pi \u003d \\ frac (3) (2) \\ pi \u003d 1 \\ frac (1) (2) \\ pi $
$ 750 ^ (\\ सर्क) \u003d 750 \\ Tales \\ Frac (1) (180) \\ pi \u003d \\ frac (25) (6) \\ pi \u003d 4 \\ frac (1) (6) \\ pi $
$ 390 ^ (\\ सर्क) \u003d 390 \\ Tales \\ Frac (1) (180) \\ pi \u003d \\ frac (13) (6) \\ pi \u003d 2 \\ frac (1) (6) \\ pi $
2. निम्नलिखित कोणों को डिग्री में कनवर्ट करें।
a) $ \\ frac (5) (4) \\ PI $
b) $ 3.12 \\ PI $
सी) 2.4 रेडियंस
फेसला
$ 180 ^ (\\ सर्क) \u003d \\ PI $
ए) $ \\ frac (5) (4) \\ pi \u003d \\ frac (5) (4) \\ Times 180 \u003d 225 ^ (\\ सर्क) $
बी) $ 3.12 \\ pi \u003d 3.12 \\ Times 180 \u003d 561.6 ^ (\\ सर्क) $
c) 1 कृपया \u003d 57.3 °
$ 2.4 \u003d \\ frac (2.4 \\ Times 57.3) (1) \u003d 137.52 $
नकारात्मक कोण और कोण $ 2 \\ PI $ रेडियन से अधिक
एक नकारात्मक कोण को सकारात्मक में बदलने के लिए, हम इसे $ 2 \\ pi $ के साथ फोल्ड करते हैं।
सकारात्मक कोण को नकारात्मक करने के लिए, हम इससे $ 2 \\ pi $ कटौती करेंगे।
उदाहरण 5।
1. $ - \\ frac (3) (4) \\ pi $ और $ - \\ frac (5) (7) \\ pi $ Radians में सकारात्मक कोण में कनवर्ट करें।
फेसला
$ 2 \\ PI $ के कोने में जोड़ें
$ - \\ frac (3) (4) \\ pi \u003d - \\ frac (3) (4) \\ pi + 2 \\ pi \u003d \\ frac (5) (4) \\ pi \u003d 1 \\ frac (1) (4) \\ पीआई $
$ - \\ frac (5) (7) \\ pi \u003d - \\ frac (5) (7) \\ pi + 2 \\ pi \u003d \\ frac (9) (7) \\ pi \u003d 1 \\ frac (2) (7) \\ पीआई $
जब वस्तु $ 2 \\ PI $ से अधिक कोण को घुमाती है; तब यह एक से अधिक सर्कल बनाता है।
इस तरह के कोण में क्रांति (मंडल या चक्र) की संख्या निर्धारित करने के लिए, हमें ऐसा नंबर मिल जाता है, जो गुणा कर रहा है कि कौन सा $ 2 \\ pi $ बराबर या उससे कम है, लेकिन इस संख्या के करीब जितना संभव हो सके।
उदाहरण 6।
1. इन कोनों में वस्तु द्वारा कवर सर्कल की संख्या का पता लगाएं
a) $ -10 \\ PI $
b) $ 9 \\ PI $
c) $ \\ frac (7) (2) \\ pi $
फेसला
a) $ -10 \\ pi \u003d 5 (-2 \\ pi) $;
$ -2 \\ pi $ घड़ी की दिशा में एक चक्र का अर्थ है, तो इसका मतलब है कि
ऑब्जेक्ट ने 5 चक्र दक्षिणावर्त बना दिया।
बी) $ 9 \\ pi \u003d 4 (2 \\ pi) + \\ pi $, $ \\ pi \u003d $ मंजिल चक्र
वस्तु ने चार और एक आधा चक्र वामावर्त बनाई
सी) $ \\ FRAC (7) (2) \\ pi \u003d 3.5 \\ pi \u003d 2 \\ pi + 1.5 \\ pi $, $ 1.5 \\ pi $ $ 3 \\ _ frac (1.5 \\ pi) के तीन तिमाहियों है (2 \\ Pi) \u003d \\ frac (3) (4)) $
ऑब्जेक्ट ने एक और तीन तिमाहियों को वामावर्त रूप से पार किया
विज्ञान की तरह त्रिकोणमिति, प्राचीन पूर्व में उत्पन्न हुई। पहला त्रिकोणमितीय अनुपात खगोलविदों द्वारा एक सटीक कैलेंडर बनाने और सितारों पर ध्यान केंद्रित करने के लिए लिया गया था। ये गणना गोलाकार त्रिकोणमिति से संबंधित थी, जबकि स्कूल के पाठ्यक्रम में, पार्टियों के अनुपात और एक फ्लैट त्रिभुज के कोण का अध्ययन किया जाता है।
त्रिकोणमिति त्रिकोणमितीय कार्यों और पार्टियों और त्रिकोणों के कोनों के बीच निर्भरता के गुणों में लगे गणित का एक वर्ग है।
पहली सहस्राब्दी की संस्कृति और विज्ञान के उदय के दौरान, ज्ञान का हमारा युग प्राचीन पूर्व से ग्रीस तक फैल गया है। लेकिन त्रिकोणमिति की मुख्य खोज अरब खलीफाट के पतियों की योग्यता है। विशेष रूप से, तुर्कमेन वैज्ञानिक अल-मारजवी ने टेंगेंट और कोटेगेंट जैसे कार्यों में प्रवेश किया, साइनस मूल्यों, स्पर्शरेगों और catangents के लिए पहली सारणी संकलित किया। भारतीय वैज्ञानिकों द्वारा साइन और कोसाइन की अवधारणा पेश की जाती है। त्रिकोणमिति पुरातनता के ऐसे महान नेताओं के लेखन में बहुत ध्यान देने के लिए समर्पित है, जैसे यूक्लिडा, आर्किमिडीज और इरैटोस्टिन।
त्रिकोणमिति के मुख्य मूल्य
संख्यात्मक तर्क के मुख्य त्रिकोणमितीय कार्य साइनस, कोसाइन, स्पर्शरेखा और canangent हैं। उनमें से प्रत्येक का अपना शेड्यूल है: साइनसॉइड, कॉसिनेडा, टैंगेंसॉयड और कैटेंजेंसॉयड।
निर्दिष्ट मात्रा के मूल्यों की गणना के लिए सूत्रों का आधार पाइथागोरो प्रमेय है। स्कूली बच्चों को शब्द में अधिक ज्ञात हैं: "पाइथागोरस पैंट, सभी दिशाओं में बराबर हैं," चूंकि सबूत समान रूप से आकार के आयताकार त्रिकोण के उदाहरण पर दिया जाता है।
साइनस, कोसाइन और अन्य निर्भरताएं किसी भी आयताकार त्रिभुज के तेज कोनों और किनारों के बीच एक लिंक स्थापित करती हैं। हम इन मूल्यों को कोण के लिए गणना करने के लिए सूत्र देते हैं और त्रिकोणमितीय कार्यों के संबंधों का पता लगाते हैं:

जैसा कि देखा जा सकता है, टीजी और सीटीजी व्यस्त कार्य हैं। यदि आप सीएटीएटी ए के साथ पाप ए और हाइपोटेनस के रूप में जमा करते हैं, और कोस ए * सी के रूप में बी रोल करते हैं, तो हमें टेंगेंट और कोटेगेंट के लिए निम्नलिखित सूत्र प्राप्त होंगे:

त्रिकोणमितीय वृत्त
ग्राफिक रूप से, कहा गया मूल्यों का अनुपात निम्नानुसार दर्शाया जा सकता है:

सर्कल, इस मामले में, सभी संभव कोण α - 0 डिग्री से 360 डिग्री तक है। जैसा कि आकृति से देखा जा सकता है, प्रत्येक फ़ंक्शन कोने मूल्य के आधार पर एक नकारात्मक या सकारात्मक मान लेता है। उदाहरण के लिए, पाप α "+" चिह्न के साथ होगा, यदि α सर्कल की तिमाही के I और II से संबंधित है, तो यह 0 डिग्री से 180 डिग्री के बीच है। Α के साथ 180 डिग्री से 360 डिग्री (III और IV क्वार्टर) से, पाप α केवल एक नकारात्मक मूल्य हो सकता है।
आइए विशिष्ट कोणों के लिए त्रिकोणमितीय तालिकाओं का निर्माण करने और मूल्यों के मूल्य को जानने का प्रयास करें।

मान α 30 डिग्री, 45 डिग्री, 60 डिग्री, 90 डिग्री, 180 डिग्री, और इसी तरह के हैं - विशेष मामलों कहा जाता है। त्रिकोणमितीय कार्यों के मूल्यों की गणना उनके लिए की जाती है और इसे विशेष तालिकाओं के रूप में प्रस्तुत की जाती है।

इन कोणों को किसी भी दुर्घटना से नहीं चुना जाता है। टेबल में पदनाम π रेडियंस के लिए खड़ा है। रेड एक कोण है जिस पर परिधि आर्क की लंबाई इसके त्रिज्या से मेल खाती है। यह मान एक सार्वभौमिक निर्भरता स्थापित करने के लिए पेश किया गया था, जब रेडियंस की गणना करते समय, सीएम में वास्तविक त्रिज्या लंबाई कोई फर्क नहीं पड़ता।

त्रिकोणमितीय कार्यों के लिए तालिकाओं में कोनों रेडियन मानों के अनुरूप हैं:

तो, यह अनुमान लगाना मुश्किल नहीं है कि 2π एक पूर्ण सर्कल या 360 डिग्री है।
त्रिकोणमितीय कार्यों की गुण: साइनस और कोसाइन
साइनस और कोसाइन, टेंगेंट और कैटेंजेंस के मुख्य गुणों पर विचार करने और तुलना करने के लिए, अपने कार्यों को आकर्षित करना आवश्यक है। यह दो आयामी समन्वय प्रणाली में स्थित एक वक्र के रूप में किया जा सकता है।
साइनसॉइड्स और कॉसिनेड्स के लिए गुणों की तुलनात्मक तालिका पर विचार करें:

| sinusoid | कोसिनुसोइड |
|---|---|
| y \u003d sin x | y \u003d cos x |
| ओडीजेड [-1; एक] | ओडीजेड [-1; एक] |
| पाप x \u003d 0, x \u003d πk पर, जहां k ε z | cos x \u003d 0, x \u003d π / 2 + πk पर, जहां k ε z |
| पाप x \u003d 1, x \u003d π / 2 + 2πk पर, जहां k ε z | cos x \u003d 1, x \u003d 2πk पर, जहां k ε z |
| पाप x \u003d - 1, x \u003d 3π / 2 + 2πk पर, जहां k ε z | cos x \u003d - 1, x \u003d π + 2πk पर, जहां k ε z |
| पाप (-x) \u003d - पाप एक्स, यानी फ़ंक्शन विषम है | cos (-x) \u003d कोस एक्स, यानी फ़ंक्शन भी है |
| समारोह आवधिक, सबसे छोटी अवधि - 2π | |
| सिन एक्स\u003e 0, एक्स-स्वामित्व वाली I और II क्वार्टर के साथ या 0 डिग्री से 180 डिग्री (2πk, π + 2πk) से | कॉस एक्स\u003e 0, एक्स-एक्स-स्वामित्व वाली आई और आईवी क्वार्टर के साथ या 270 डिग्री से 9 0 डिग्री (- π / 2 + 2πk, π / 2 + 2πk) |
| सीन एक्स \u003c0, एक्स-एक्स-स्वामित्व वाली III और IV क्वार्टर के साथ या 180 डिग्री से 360 डिग्री (π + 2πk, 2π + 2πk) | एक्स-एक्स और तीसरे तिमाहियों के साथ या 90 डिग्री से 270 डिग्री (π / 2 + 2πk, 3π / 2 + 2πk) के साथ |
| अंतराल पर बढ़ता है [- π / 2 + 2πk, π / 2 + 2πk] | अंतराल पर बढ़ता है [-π + 2πk, 2πk] |
| अंतराल में कमी [π / 2 + 2πk, 3π / 2 + 2πk] | अंतराल पर घटता है |
| व्युत्पन्न (sin x) '\u003d cos x | व्युत्पन्न (कोस एक्स) '\u003d - पाप एक्स |
यह निर्धारित करें कि फ़ंक्शन भी बहुत आसान है या नहीं। त्रिकोणमितीय मूल्यों के संकेतों के साथ एक त्रिकोणमितीय सर्कल को प्रस्तुत करने के लिए पर्याप्त है और बैल अक्ष के सापेक्ष शेड्यूल को मानसिक रूप से "फोल्ड" किया गया है। यदि संकेत मेल खाते हैं, तो फ़ंक्शन भी है, अन्यथा - एक अजीब।

रेडियंस का परिचय और साइनसॉइड्स और कोसिनेड्स के मुख्य गुणों के हस्तांतरण के लिए आपको निम्नलिखित नियमितता लाने की अनुमति मिलती है:

सुनिश्चित करें कि सूत्र बहुत आसान है। उदाहरण के लिए, x \u003d π / 2 साइनस के लिए 1, साथ ही साथ कोसाइन एक्स \u003d 0. के लिए आप तालिकाओं की जांच कर सकते हैं या निर्दिष्ट मूल्यों के लिए कार्यों के कार्यों का पता लगा सकते हैं।
Tangensoids और Kotangensoids की गुण
टेंगेंट और कोटेंगेंट के कार्यों के ग्राफ साइनसॉइड्स और कॉसिनेड्स से काफी भिन्न होते हैं। टीजी और सीटीजी के मूल्य एक दूसरे के लिए वापस आ गए हैं।


- Y \u003d tg x।
- Tangentoid x \u003d π / 2 + πk पर y मान करता है, लेकिन कभी भी उन तक नहीं पहुंचता है।
- टैंगेंसॉयड की सबसे कम सकारात्मक अवधि π के बराबर है।
- टीजी (- एक्स) \u003d - टीजी एक्स, यानी, फ़ंक्शन विषम है।
- Tg x \u003d 0, x \u003d πk पर।
- समारोह बढ़ रहा है।
- टीजी एक्स\u003e 0, एक्स ε (πk, π / 2 + πk) पर।
- टीजी एक्स \u003c0, एक्स ε (- π / 2 + πk, πk) पर।
- व्युत्पन्न (tg x) '\u003d 1 / cos 2 \u2061x।
पाठ के नीचे catangensoids की ग्राफिक छवि पर विचार करें।

Kotangensoids के मुख्य गुण:
- Y \u003d ctg x।
- साइनस और कोसाइन के कार्यों के विपरीत, टैंगेंटोइड वाई में, यह कई वैध संख्याओं के मान ले सकता है।
- कोठंगेंसोइड x \u003d πk पर y मान करता है, लेकिन कभी भी उन तक नहीं पहुंचता है।
- Catangensoid की सबसे छोटी सकारात्मक अवधि π के बराबर है।
- सीटीजी (- एक्स) \u003d - सीटीजी एक्स, यानी फ़ंक्शन विषम है।
- Ctg x \u003d 0, x \u003d π / 2 + πk पर।
- समारोह उतर रहा है।
- सीटीजी एक्स\u003e 0, एक्स ε (πk, π / 2 + πk) पर।
- सीटीजी एक्स \u003c0, एक्स ε (π / 2 + πk, πk) पर।
- व्युत्पन्न (ctg x) '\u003d - 1 / sin 2 \u2061x फिक्स
ओए और ओबी के विभिन्न बीम की एक जोड़ी, एक बिंदु ओ से उभरती है, को कोण कहा जाता है और प्रतीक (ए, बी) द्वारा इंगित किया जाता है। बिंदु ओ को कोण की चोटी कहा जाता है, और यूबी यूबी की किरण - कोण के किनारे। यदि ए और बी - ओए और ओबी किरणों के दो बिंदु, तो (ए, बी) को एओएस (चित्र 1.1) के प्रतीक से भी संकेत दिया जाता है।
कोण (ए, बी) को विस्तारित कहा जाता है अगर ओए और ओबी की किरणें एक बिंदु से उभरती हैं, एक सीधे एक पर झूठ बोलती हैं और मेल नहीं खाते हैं (जो विपरीत रूप से निर्देशित) है।

अंजीर ..1.1
दो कोण को बराबर माना जाता है यदि एक कोण दूसरे पर लागू किया जा सकता है ताकि कोनों का पक्ष संयोग हो। द्विभाजक कोण को कोण के शीर्ष पर शुरुआत के साथ एक बीम कहा जाता है, जिससे कोण को दो बराबर कोनों में विभाजित किया जाता है।
ऐसा कहा जाता है कि ओएस की किरण, कोण एओ के शीर्ष से आ रही है, अगर यह एवी (अंजीर 1.2) के खंड को पार करती है तो इसकी पार्टियों के बीच निहित है। ऐसा कहा जाता है कि बिंदु सी कोण के किनारों के बीच स्थित है, अगर इस बिंदु के माध्यम से इस बिंदु के माध्यम से कोण के शीर्ष पर शुरू किया जा सकता है, जो कोने के पक्षों के बीच झूठ बोलता है। कोण के किनारों के बीच झूठ बोलने वाले विमान के सभी बिंदुओं का सेट कोण का एक आंतरिक क्षेत्र (चित्र 1.3) बनाता है। विमान के बिंदुओं का सेट जो आंतरिक क्षेत्र से संबंधित नहीं है और कोण के किनारे कोण का बाहरी क्षेत्र बनाता है।
एक कोण (ए, बी) को अधिक कोण (सी, डी) माना जाता है यदि कोण (सी, डी) को कोण (ए, बी) पर लगाया जा सकता है ताकि पक्षों की एक जोड़ी के संयोजन के बाद, दूसरा पक्ष कोण (सी, डी) कोण (ए, बी) के किनारों के बीच झूठ होगा। अंजीर में। 1.4 एओएस अधिक एओएस।
कोण (ए, बी) (छवि 1.5) के किनारों के बीच झूठ के साथ बीम दें। किरणों के जोड़े ए, सी और सी, बी दो कोनों का निर्माण करते हैं। कोण के बारे में (ए, बी) वे कहते हैं कि यह दो कोणों (ए, सी) और (सी, बी) का योग है, और लिखते हैं: (ए, बी) \u003d (ए, सी) + (सी, बी) ।

अंजीर .1.3
आमतौर पर ज्यामिति में वे तैनात से छोटे कोणों से निपटते हैं। हालांकि, दो कोणों के अतिरिक्त के परिणामस्वरूप, एक कोण को और अधिक तैनात किया जा सकता है। इस मामले में, विमान का हिस्सा, जिसे कोण का आंतरिक क्षेत्र माना जाता है, को चाप के साथ चिह्नित किया जाता है। अंजीर में। 1.6 ए कोण एओएस के अंदर, एओसी और ओवी के कोणों के अतिरिक्त और अधिक तैनात के परिणामस्वरूप प्राप्त किया जाता है, चाप द्वारा चिह्नित किया जाता है।

चित्र .1.5।
बड़ी 360 डिग्री के कोण भी हैं। ऐसे कोण बनते हैं, उदाहरण के लिए, विमान प्रोपेलर के घूर्णन, ड्रम के घूर्णन, जिस पर रस्सी घाव है, और इसी तरह।
भविष्य में, प्रत्येक कोण पर विचार करते समय, हम इस कोण के किनारों में से एक को अपनी प्रारंभिक पार्टी से मानने के लिए सहमत होते हैं, और दूसरा अंतिम पार्टी है।
कोई भी कोण, उदाहरण के लिए, एओएस (चित्र 1.7) का कोण, कोण (ओए) के प्रारंभिक पक्ष के शीर्ष पक्ष (ओं) के शीर्ष पक्ष के चारों ओर जंगम बीम के घूर्णन के परिणामस्वरूप प्राप्त किया जा सकता है। हम इस कोण को मापेंगे, बिंदु ओ के चारों ओर क्रांति की पूरी संख्या में विचार करते हुए, साथ ही साथ जिस दिशा में घूर्णन हुआ।
सकारात्मक और नकारात्मक कोण।
हमारे पास ओए और ओआई (FIG.1.8) की किरणों द्वारा गठित एक कोण है। चलने योग्य किरण, अपनी प्रारंभिक स्थिति (ओए) से बिंदु ओ के चारों ओर घूमती है, घूर्णन के दो अलग-अलग दिशाओं में अंतिम स्थिति (ओं) ले सकती है। ये निर्देश संबंधित तीरों के साथ चित्रा 1.8 में दिखाए जाते हैं।

अंजीर .1.7

बस एक संख्यात्मक अक्ष पर, दो दिशाओं में से एक को सकारात्मक माना जाता है, और दूसरा नकारात्मक है, चलने योग्य बीम के घूर्णन के दो अलग-अलग दिशाओं को प्रतिष्ठित किया जाता है। यह रोटेशन की सकारात्मक दिशा माना जाने पर सहमत हो गया था कि दिशा जो दक्षिणावर्त की घूर्णन की दिशा के विपरीत है। घूर्णन की दिशा घड़ी की दिशा में घूर्णन की दिशा के साथ मेल खाती है, को नकारात्मक माना जाता है।
इन परिभाषाओं के अनुसार, कोण भी सकारात्मक और नकारात्मक में विभाजित होते हैं।
सकारात्मक कोण को सकारात्मक दिशा में शुरुआती बिंदु के चारों ओर चलने वाले बीम के घूर्णन द्वारा गठित कोण कहा जाता है।

चित्रा 1.9 में कुछ सकारात्मक कोण हैं। (चलने योग्य बीम के घूर्णन की दिशा तीर के चित्रों में दिखाया गया है।)
एक नकारात्मक कोण को नकारात्मक दिशा में शुरुआती बिंदु के आसपास चलने वाले बीम के घूर्णन द्वारा गठित कोण कहा जाता है।
चित्रा 1.10 कुछ नकारात्मक कोण दिखाता है। (चलने योग्य बीम के घूर्णन की दिशा तीर के चित्रों में दिखाया गया है।)

लेकिन दो संयोग वाली किरणें भी बन सकती हैं और + 360 डिग्री पी और -360 डिग्री सेल्सियस (एन \u003d 0,1,2,3, ...) के कोण भी हो सकती हैं। रोटेशन के सबसे छोटे संभावित गैर-नकारात्मक कोण का उपयोग करके निरूपित करें, जो ओए रे को ओएस स्थिति में स्थानांतरित कर रहा है। यदि अब ओवी की किरण को बिंदु ओ के चारों ओर एक पूर्ण मोड़ दिया जाता है, तो हमें कोण का एक और मूल्य मिलता है, अर्थात्: एवीओ \u003d बी + 360 डिग्री।
सर्कल आर्क के कोनों का मापन। आर्क और कोनों के माप की इकाइयाँ
कुछ मामलों में, यह सर्कल आर्क का उपयोग करके कोणों को मापने के लिए सुविधाजनक साबित होता है। इस तरह के माप की संभावना प्रतिलिपि के प्रसिद्ध प्रस्ताव पर आधार है कि केंद्रीय कोण और संबंधित आर्क उन पर प्रत्यक्ष आनुपातिक निर्भरता में हैं, जो एक सर्कल में हैं।
इस सर्कल के कुछ चाप को आर्क के माप की प्रति इकाई अपनाई गई। इस चाप से संबंधित केंद्रीय कोण कोणों के माप की इकाई ले जाएगा। इस स्थिति के साथ, इस चाप के अनुरूप किसी भी परिधि चाप और इसी केंद्रीय कोण में माप इकाइयों की समान संख्या होगी। इसलिए, सर्कल आर्क मापने, इन चापों के अनुरूप केंद्रीय कोनों की परिमाण निर्धारित करना संभव है।
चाप और कोणों को मापने के लिए दो सबसे आम प्रणालियों पर विचार करें।
डिग्री मापने कोनों
कोणों के माप की मुख्य इकाई के रूप में कोणों के एक डिग्री माप के दौरान (संदर्भ कोण, जिसके साथ विभिन्न कोणों की तुलना की जाती है) एक कोण को एक डिग्री (नामित 1?) में लिया जाता है। एक डिग्री का कोण विस्तारित कोण के 1/180 के बराबर कोण है। 1 डिग्री के कोण के 1/60 के बराबर एक कोण एक मिनट (नामित 1 ") का कोण है। एक मिनट में कोण के 1/60 हिस्से के बराबर कोण एक सेकंड (नामित 1") में एक कोण होता है।
रेडियन कॉर्नर माप माप
ज्यामिति और त्रिकोणमिति में कोणों के डिग्री माप माप के साथ, अन्य माप माप का भी उपयोग किया जाता है, जिसे रेडियन कहा जाता है। ओ के केंद्र के साथ त्रिज्या आर के सर्कल पर विचार करें। हम एक और ओबी के बारे में दो त्रिज्या करेंगे ताकि एवी चाप की लंबाई सर्कल त्रिज्या (चित्र 1.12) के बराबर हो। एक ही समय में प्राप्त एओएस का केंद्रीय कोण एक रेडियन का कोण होगा। 1 रेडियन का कोण रेडिकुलर मापन माप माप के माप की प्रति इकाई अपनाया जाता है। जब कोण रेडिक होते हैं, तो विस्तृत कोण आर रेडियंस के बराबर होता है।

कोणों के माप की डिग्री और रेडियन इकाइयां बराबरता से जुड़ी होती हैं:
1 रेडियन \u003d 180? / P57 ° 17 "45"; 1? \u003d पी / 180 radian0.017453radian;
1 "\u003d पी / 180 * 60 radian0.000291 रेडियन;
1 "" \u003d आर / 180 * 60 * 60 Radian0.000005 रेडियन।
कोण की डिग्री (या रेडियन) माप को कोने भी कहा जाता है। एओएस का कोण मूल्य कभी-कभी अस्वीकृत होता है /
कोनों का वर्गीकरण
90 डिग्री के बराबर एक कोण, या पी / 2 के रेडिकुलर माप में, को एक प्रत्यक्ष कोण कहा जाता है; इसे अक्सर पत्र डी द्वारा दर्शाया जाता है। 90 डिग्री से कम कोण को तेज कहा जाता है; 90 डिग्री से अधिक कोण, लेकिन छोटे 180 डिग्री को बेवकूफ कहा जाता है।
एक आम तरफ दो कोणों और 180 डिग्री घटकों की मात्रा में आसन्न कोण कहा जाता है। दो कोणों में एक आम तरफ और 90 डिग्री घटकों की मात्रा में अतिरिक्त कोनों कहा जाता है।
त्रिकोणमितीय सर्कल पर कोनों की गिनती।
ध्यान!
इस विषय में अतिरिक्त है
एक विशेष खंड 555 में सामग्री।
उन लोगों के लिए जो दृढ़ता से "बहुत नहीं ..."
और उन लोगों के लिए जो "बहुत ..." हैं)
वह पिछले पाठ में लगभग समान है। कुल्हाड़ी, सर्कल, कोण, सभी रैंक चिनार हैं। जोड़ा चौथाई (एक बड़े वर्ग के कोनों में) - पहले से चौथे से। और फिर क्या होगा अगर किसी को नहीं पता? जैसा कि आप देख सकते हैं, एक चौथाई (उन्हें दक्षिणावर्त के दौरान खूबसूरत शब्द "चतुर्भुज" भी कहा जाता है)। कुल्हाड़ियों पर जोड़ा कोण मान। सब कुछ स्पष्ट है, कोई समस्या नहीं है।
और हरा तीर जोड़ा गया है। एक प्लस के साथ। इसका क्या मतलब है? मुझे आपको याद दिलाता है कि कोने का स्थिर पक्ष हमेशा यह सकारात्मक सेमी-अक्ष के लिए खा रहा है ओह। तो, अगर हम कोण के चलते पक्ष को बदल देंगे एक प्लस के साथ तीर पर। आरोही क्वार्टा संख्या, कोण को सकारात्मक माना जाएगा। उदाहरण के लिए, चित्र एक सकारात्मक कोण + 60 डिग्री दिखाता है।
अगर हम कोनों को पकड़ते हैं विपरीत दिशा में, दक्षिणावर्त तीर के साथ, कोण को नकारात्मक माना जाएगा। तस्वीर पर माउस (या टैबलेट पर चित्र टैप करें), एक शून्य के साथ नीले तीर को देखें। यह कोनों के नकारात्मक संदर्भ की दिशा है। उदाहरण के लिए, एक नकारात्मक कोण दिखाया गया है (60 डिग्री)। और आप देखेंगे कि अक्ष पर diquses कैसे बदल गया है ... मैंने उन्हें नकारात्मक कोणों में भी स्थानांतरित कर दिया। संख्या चतुर्भुज नहीं बदलता है।
यहां, आमतौर पर, पहली गलतफहमी शुरू होती है। ऐसा कैसे!? और यदि सर्कल पर नकारात्मक कोण सकारात्मक के साथ मेल खाता है!? और सामान्य रूप से, यह पता चला है कि, चलने योग्य पक्ष की समान स्थिति (या संख्यात्मक सर्कल पर बिंदु) को नकारात्मक कोण और सकारात्मक कहा जा सकता है!?
हाँ। बिल्कुल सही। मान लें कि एक सर्कल पर 90 डिग्री का एक सकारात्मक कोण है बिल्कुल वैसा ही स्थिति शून्य से 270 डिग्री में एक नकारात्मक कोण के रूप में है। सकारात्मक कोण, उदाहरण के लिए, + 110 डिग्री डिग्री पर कब्जा है बिल्कुल वैसा ही नकारात्मक कोण -250 डिग्री के रूप में स्थिति।
कोई दिक्कत नहीं है। ऊपर सही ढंग से।) कोण के सकारात्मक या नकारात्मक कैलकुस की पसंद कार्य की स्थिति पर निर्भर करता है। अगर कुछ भी स्थिति में नहीं कहा जाता है खुला पाठ कोने के संकेत के बारे में, (टाइप "सबसे छोटा निर्धारित करने के लिए सकारात्मक कोने ", आदि), हम आरामदायक मूल्यों के साथ काम करते हैं।
सिवाय इसके कि (और उनके बिना कैसे?!) त्रिकोणमितीय असमानताएं हैं, लेकिन वहां हम इस चिप को निपुण करेंगे।
और अब आप सवाल करते हैं। मैंने कैसे पहचान लिया कि 110 डिग्री के कोण की स्थिति कोण -250 डिग्री की स्थिति के साथ मेल खाती है?
उपनाम जो यह पूरी बारी के कारण है। 360 डिग्री पर ... स्पष्ट नहीं है? फिर एक सर्कल बनाएं। हम कागज पर आकर्षित करते हैं। हम कोने को चिह्नित करते हैं के बारे में 110 °। तथा विचार करेंयह पूर्ण कारोबार में कितना बनी हुई है। यह केवल 250 ° रहेगा ...
पकड़ा हुआ? और अब - ध्यान दें! यदि कोण 110 ° और -250 ° एक सर्कल में हैं वही
स्थिति, क्या? हाँ, कि कोण 110 डिग्री और -250 डिग्री हैं पूरी तरह से समान
साइनस, कोसीनस, टेंगेंट और कॉटेंगेंट!
वे। SIN110 ° \u003d पाप (-250 डिग्री), सीटीजी 110 डिग्री \u003d सीटीजी (-250 डिग्री) और इसी तरह। यह पहले से ही वास्तव में महत्वपूर्ण है! और अपने आप में - बहुत सारे कार्य हैं, जहां अभिव्यक्तियों को सरल बनाना, और त्रिकोणमिति के सूत्रों और अन्य ज्ञान के सूत्रों के बाद के विकास के आधार के रूप में आवश्यक है।
स्पष्ट मामला, 110 डिग्री और -250 ° मैंने वैकल्पिक रूप से उदाहरण के लिए नेमम लिया। ये सभी समानताएं किसी भी कोनों के लिए काम करती हैं जो सर्कल में एक स्थिति पर कब्जा करती हैं। 60 डिग्री और -300 डिग्री, -75 डिग्री और 285 डिग्री, और इसी तरह। मैं तुरंत नोट करता हूं कि इन जोड़ों में कोण - विभिन्न। और यहां उनके त्रिकोणमितीय कार्य हैं - वही।
मुझे लगता है कि ऐसे नकारात्मक कोण आप समझते हैं। यह काफी सरल है। दक्षिणावर्त प्रगति के खिलाफ - एक सकारात्मक उलटी गिनती। पाठ्यक्रम में - नकारात्मक। कोण सकारात्मक, या नकारात्मक पढ़ें हम पर निर्भर करता है। हमारी इच्छा से। खैर, और कार्य से, निश्चित रूप से ... मुझे आशा है कि आप समझते हैं और नकारात्मक कोणों से सकारात्मक और पीठ तक त्रिकोणमितीय कार्यों में कैसे आगे बढ़ना है। एक सर्कल, एक अनुमानित कोण खींचें, लेकिन देखें कि पूर्ण कारोबार तक कितना कमी है, यानी 360 ° तक।
कोनों 360 डिग्री से अधिक हैं।
कोनों जो 360 डिग्री से अधिक हैं। क्या कोई ऐसा है? निश्चित रूप से हैं। उन्हें एक सर्कल में कैसे आकर्षित करें? हाँ, कोई समस्या नहीं है! मान लीजिए हमें समझने की जरूरत है कि किस तिमाही को 1000 डिग्री का कोण मिलेगा? सरलता! हम दक्षिणावर्त के समय के खिलाफ एक पूर्ण मोड़ बनाते हैं (कोण सकारात्मक दिया गया था!)। 360 ° चले गए। अच्छा, और हवा पर! एक और मोड़ - पहले से ही यह 720 डिग्री बदल गया। कितना बचा है? 280 °। एक पूर्ण मोड़ के लिए पर्याप्त नहीं है ... लेकिन कोण 270 डिग्री से अधिक है - और यह तीसरी और चौथी तिमाही के बीच की सीमा है। यह 1000 डिग्री में हमारा कोण चौथी तिमाही में प्रवेश करता था। हर एक चीज़।
जैसा कि आप देख सकते हैं, यह काफी आसान है। एक बार फिर मैं आपको याद दिलाता हूं कि कोण 1000 डिग्री और 280 डिग्री का कोण है, जिसे हम "अनावश्यक" पूर्ण क्रांति को त्यागने के माध्यम से प्राप्त हुए - यह सख्ती से बोल रहा है, भिन्न हो कोनों। लेकिन इन कोनों के त्रिकोणमितीय कार्यों पूरी तरह से समान! वे। SIN1000 ° \u003d SIN280 °, COS1000 ° \u003d COS280 °, आदि अगर मैं साइनस होता, तो मैं इन दो कोनों के बीच अंतर नहीं देखूंगा ...
आपको यह सब क्यों चाहिए? हमें कोनों को एक से दूसरे में अनुवाद करने की आवश्यकता क्यों है? हां, सब कुछ समान है।) अभिव्यक्ति को सरल बनाने के लिए। अभिव्यक्ति का सरलीकरण, वास्तव में, स्कूल गणित का मुख्य कार्य। खैर, वैसे, सिर प्रशिक्षण है।)
अच्छा, अभ्यास?)
सवालों के जवाब देने। पहला सरल।
1. कॉर्नर -325 ° गिरता है?
2. 3000 ° गिरने का कोण क्या है?
3. कोण -3000 ° कितनी तिमाही में गिरावट आती है?
एक समस्या है? या अनिश्चितता? हम धारा 555, एक त्रिकोणमितीय सर्कल के साथ व्यावहारिक काम पर जाते हैं। वहां, पहले पाठ में यह बहुत "व्यावहारिक काम ..." सब कुछ विस्तृत है ... में ऐसा असुरक्षा के मुद्दे नहीं!
4. SIN555 ° क्या संकेत है?
5. टीजी 555 डिग्री क्या संकेत है?
परिभाषित? अति उत्कृष्ट! संदेह? धारा 555 के लिए आवश्यक है ... वैसे, वे सीखेंगे कि एक त्रिकोणमितीय सर्कल पर टेंगेंट और कॉटनेंट कैसे आकर्षित किया जाए। बहुत उपयोगी बात है।
और अब रूट में सवाल।
6. सबसे छोटे सकारात्मक कोण के साइनस को sin777 ° अभिव्यक्ति को प्रमाणित करें।
7. सबसे बड़ा नकारात्मक कोण के कोसाइन को एक अभिव्यक्ति COS777 डिग्री बनाएं।
8. सबसे छोटे सकारात्मक कोण के Cacinus को सीओएस अभिव्यक्ति (-777 डिग्री) प्रदान करें।
9. उच्चतम नकारात्मक कोण के साइनस को sin777 ° अभिव्यक्ति को प्रमाणित करें।
क्या, 6-9 सवाल क्या है? परीक्षा में, इस तरह के शब्द नहीं मिलते हैं ... तो हो, मैं अनुवाद करूंगा। सिर्फ तुम्हारे लिए!
शब्द "एक अभिव्यक्ति लाते हैं ..." का अर्थ एक अभिव्यक्ति को परिवर्तित करने के लिए करता है ताकि उसका मूल्य हो परिवर्तित नहीं और उपस्थिति कार्य के अनुसार बदल गई है। तो, कार्य 6 और 9 में हमें साइनस मिलना चाहिए, जिसके भीतर यह लागत म्यूट पॉजिटिव कॉर्नर। बाकी सब कुछ - इससे कोई फर्क नहीं पड़ता।
उत्तर क्रम में जारी किए जाएंगे (हमारे नियमों का उल्लंघन)। और क्या करना है, संकेत केवल दो है, और तिमाही केवल चार है ... आप विकल्पों में नहीं चलेगा।
6. SIN57 °।
7. कॉस (-57 °)।
8. COS57 °।
9. -सिन (-57 °)
मुझे लगता है कि प्रश्नों के उत्तर 6 -9 किसी ने उलझन में। विशेष -सिन (-57 °)क्या यह सच है?) दरअसल, संदर्भ कोनों के प्राथमिक नियमों में त्रुटियों के लिए एक जगह है ... यही कारण है कि मुझे एक सबक करना पड़ा: "कार्यों के संकेतों की पहचान कैसे करें और कोनों को त्रिकोणमितीय सर्कल पर लाएं? " धारा 555 में। 4 से 9 कार्यों को अलग किया गया है। सभी पानी के नीचे पत्थरों के साथ, अच्छी तरह से disassembled। और वे यहाँ हैं।)
अगले पाठ में, हम रहस्यमय रेडियंस और संख्या "पीआई" से निपटेंगे। हम रेडियंस और पीठ में डिग्री आसानी से और सही ढंग से अनुवाद करना सीखेंगे। और आश्चर्य के साथ आप पाएंगे कि साइट पर यह प्राथमिक जानकारी पहले से ही पकड़ लेता है कुछ गैर-मानक त्रिकोणमिति कार्यों को हल करने के लिए!
अगर आपको यह साइट पसंद है ...
वैसे, मेरे पास आपके लिए एक और कुछ दिलचस्प साइटें हैं।)
इसे उदाहरणों को हल करने और अपने स्तर को खोजने में पहुंचा जा सकता है। तत्काल चेक के साथ परीक्षण। जानें - ब्याज के साथ!)
आप सुविधाओं और डेरिवेटिव से परिचित हो सकते हैं।
त्रिकोणमिति में, एक महत्वपूर्ण अवधारणा है रोटेशन का कोण। नीचे हम लगातार घूर्णन का एक विचार देंगे, और सभी संगत अवधारणाओं को दर्ज करेंगे। चलो मोड़ की सामान्य प्रस्तुति के साथ शुरू करते हैं, चलो पूर्ण मोड़ के बारे में कहते हैं। इसके बाद, हम घूर्णन के कोण की अवधारणा के लिए आगे बढ़ते हैं और इसकी मुख्य विशेषताओं, जैसे दिशा और घूर्णन की परिमाण पर विचार करते हैं। अंत में, हम बिंदु के चारों ओर आकृति के आकार की परिभाषा देंगे। पाठ पर सभी सिद्धांत व्याख्यात्मक उदाहरणों और ग्राफिक चित्रों के साथ आपूर्ति की जाएगी।
नेविगेटिंग पेज।
बिंदु के चारों ओर बिंदु को मोड़ना क्या कहा जाता है?
तत्काल, हम ध्यान देते हैं कि "बिंदु के चारों ओर मुड़ें" वाक्यांश के साथ हम "बिंदु के चारों ओर मुड़ें" और "बिंदु के सापेक्ष बारी" वाक्यांश का भी उपयोग करेंगे, जिसका अर्थ समान है।
हम परिचय देते हैं बिंदु के चारों ओर बिंदु की घूर्णन की अवधारणा.
सबसे पहले हम रोटेशन के केंद्र की परिभाषा देते हैं।
परिभाषा।
बिंदु सापेक्ष जिसके लिए मोड़ जाता है उसे बुलाया जाता है टर्निंग सेंटर.
अब मान लें कि बिंदु के घूर्णन के परिणामस्वरूप क्या प्राप्त होता है।
किसी बिंदु के घूर्णन के परिणामस्वरूप ओ को मोड़ने के केंद्र के सापेक्ष, बिंदु 1 प्राप्त होता है (जो एक निश्चित राशि के मामले में ए के साथ मेल खा सकता है), और बिंदु ए 1 के साथ सर्कल पर निहित है ओए त्रिज्या बिंदु पर केंद्र। दूसरे शब्दों में, बिंदु के सापेक्ष मोड़ने पर एक प्रक्रिया को 1 को बिंदु पर इंगित करते हैं, जो ओए त्रिज्या बिंदु पर केंद्र के साथ सर्कल पर झूठ बोलते हैं।
ऐसा माना जाता है कि जब वह अपने चारों ओर मुड़ गया तो बिंदु ओ खुद में चला जाता है। यह घूर्णन के केंद्र के चारों ओर घूमने के परिणामस्वरूप है, बिंदु ओ खुद में जाता है।
यह भी ध्यान देने योग्य है कि बिंदु के चारों ओर घूर्णन बिंदु ओ को ओए त्रिज्या बिंदु पर केंद्र के साथ सर्कल के चारों ओर बिंदु के आंदोलन के परिणामस्वरूप आगे बढ़ना चाहिए।
स्पष्टता के लिए, हम नीचे दिए गए आंकड़ों में बिंदु और बिंदु के घूर्णन का एक उदाहरण प्रस्तुत करते हैं, बिंदु ए को बिंदु को 1 पर ले जाएं, हम एक तीर की मदद से दिखाते हैं।
पूर्ण मोड़
आप बारी ओ के केंद्र के सापेक्ष बिंदु के इस तरह के घूर्णन कर सकते हैं, जो एक बिंदु, सर्कल के सभी बिंदुओं को पारित करने के बाद, एक ही स्थान पर हो जाएगा। उसी समय वे कहते हैं कि बिंदु ओ के आसपास एक पूरा हुआ।
आइए एक पूर्ण कारोबार का ग्राफिक चित्रण दें।

यदि आप एक मोड़ पर नहीं रुकते हैं, लेकिन परिधि के चारों ओर बिंदु के आंदोलन को जारी रखने के लिए, तो आप पूर्ण क्रांति पर दो, तीन और इतने प्रदर्शन कर सकते हैं। नीचे दिए गए ड्राइंग में दिखाता है कि कैसे दो पूर्ण मोड़ का उत्पादन किया जा सकता है, और बाईं ओर तीन मोड़ है।

रोटेशन कोण की अवधारणा
पहले पैराग्राफ में पेश किए गए बिंदु से, घूर्णन का बिंदु स्पष्ट है कि बिंदु के घूर्णन के बिंदुओं का एक अनंत सेट और बिंदु ओ के आसपास। दरअसल, ओए त्रिज्या बिंदु पर केंद्र के साथ परिधि के किसी भी बिंदु को बिंदु के घूर्णन के परिणामस्वरूप एक बिंदु 1 के रूप में माना जा सकता है। इसलिए, दूसरे से एक मोड़ को अलग करने के लिए, पेश किया गया रोटेशन कोण की अवधारणा.
घूर्णन के कोण की विशेषताओं में से एक है बारी दिशा। घूर्णन की दिशा में, न्यायाधीश कैसे बिंदु का घूर्णन किया जाता है - दक्षिणावर्त या वामावर्त।
रोटेशन के कोण की एक और विशेषता है मूल्य। घूर्णन के कोणों को समान इकाइयों में मापा जाता है: सबसे आम डिग्री और रेडियंस। यह ध्यान देने योग्य है कि रोटेशन का कोण किसी भी वास्तविक संख्या से अनंतता के अंतराल से किसी भी वास्तविक संख्या से व्यक्त किया जा सकता है, जो ज्यामिति में कोने के विपरीत, जिसका मूल्य डिग्री में सकारात्मक होता है और नहीं होता है 180 से अधिक।
घूर्णन के कोणों को संदर्भित करने के लिए, ग्रीक वर्णमाला के लोअरकेस अक्षरों का आमतौर पर उपयोग किया जाता है: आदि मोड़ के एक बड़ी संख्या को संदर्भित करने के लिए, लोअर इंडेक्स के साथ एक अक्षर अक्सर उपयोग करता है, उदाहरण के लिए, ![]() .
.
अब चलो घूर्णन के कोण की विशेषताओं के बारे में बात करते हैं और क्रम में।
बारी दिशा
बिंदु पर केंद्र के साथ सर्कल को अंक ए और ए 1 चिह्नित करने दें। बिंदु ए 1 पर, आप किसी भी घड़ी की दिशा में या विपरीत दिशा में केंद्र के चारों ओर घूमकर बिंदु ए से प्राप्त कर सकते हैं। इन मोड़ों को तार्किक रूप से अलग माना जाता है।
हम सकारात्मक और नकारात्मक दिशा में मोड़ों को चित्रित करते हैं। नीचे ड्राइंग में, मोड़ सकारात्मक दिशा में और दाईं ओर - नकारात्मक में दिखाया गया है।

रोटेशन के कोण की परिमाण, मनमानी का एक कोण
घूर्णन के केंद्र के अलावा बिंदु के घूर्णन कोण को इसके मूल्य के संकेत से पूरी तरह से निर्धारित किया जाता है, दूसरी तरफ, मोड़ के कोने का मूल्य यह तय किया जा सकता है कि यह मोड़ कैसे किया गया था।
जैसा कि हम पहले से ही ऊपर वर्णित हैं, डिग्री में घूर्णन के कोण की परिमाण को संख्या से + ∞ तक की संख्या व्यक्त की जाती है। इस मामले में, प्लस साइन घड़ी की दिशा में बदल जाता है, और शून्य संकेत वामावर्त घूर्णन कर रहा है।
अब यह रोटेशन के कोण के मूल्य के बीच एक पत्राचार स्थापित करना बाकी है और तथ्य यह है कि यह किससे मेल खाती है।
चलो शून्य डिग्री के बराबर रोटेशन के कोण के साथ शुरू करते हैं। यह कोने बिंदु और अपने आप में आंदोलन बदल जाता है। दूसरे शब्दों में, बिंदु के चारों ओर 0 डिग्री चालू करते समय ओ के स्थान पर एक बचे रहते हैं।
बिंदु के घूर्णन पर जाएं और बिंदु ओ के आसपास, जिसमें घूर्णन कारोबार के आधे हिस्से के भीतर होता है। हम मान लेंगे कि बिंदु ए 1 को इंगित करता है। इस मामले में, डिग्री में एओए 1 का पूर्ण कोण 180 से अधिक नहीं है। यदि सकारात्मक दिशा में घूर्णन हुआ, तो घूर्णन के कोण की परिमाण को एओए 1 के कोण के बराबर माना जाता है, और यदि नकारात्मक दिशा में घूर्णन हुआ, तो इसका मूल्य एओए के कोण के बराबर माना जाता है। 1 एक माइनस साइन के साथ। उदाहरण के लिए, हम एक ड्राइंग प्रस्तुत करते हैं जो 30, 180 और -150 डिग्री के घूर्णन के कोण दिखाते हैं।

रोटेशन के कोण बड़े होते हैं 180 डिग्री और छोटे -180 डिग्री निम्नलिखित पर्याप्त रूप से स्पष्ट के आधार पर निर्धारित होते हैं क्रमिक मोड़ की गुण: केंद्र के चारों ओर एक बिंदु के कई सीरियल मोड़ एक बारी के बराबर हैं, जिसका मूल्य इन मोड़ों के मूल्यों के बराबर है।
आइए इस संपत्ति को चित्रित करने का एक उदाहरण दें। हम बिंदु को 45 डिग्री बिंदु के सापेक्ष बिंदु को घुमाएंगे, और फिर इस बिंदु को 60 डिग्री तक चालू करेंगे, जिसके बाद हम इस बिंदु को -35 डिग्री तक बदलते हैं। इन इंटरमीडिएट पॉइंट्स को 1, 2 और 3 के रूप में बदल देता है। उसी बिंदु और 3 में, हम 45 + 60 + (- 35) \u003d 70 डिग्री के कोण के बिंदु के एक मोड़ को निष्पादित करके प्राप्त कर सकते थे।

इसलिए, रोटेशन के कोण, बड़ी 180 डिग्री, हम कोनों पर लगातार कुछ मोड़ के रूप में प्रतिनिधित्व करेंगे, जिनमें से मूल्यों का योग रोटेशन के प्रारंभिक कोण का मूल्य देता है। उदाहरण के लिए, 279 डिग्री के रोटेशन का कोण 180 और 99 डिग्री, या 9 0, 9 0, 9 0, 9 0 और 9 डिग्री, या 180, 180 और -81 डिग्री, या 279 लगातार 1 डिग्री के 279 के अनुक्रमिक मोड़ से मेल खाता है।
घूर्णन के कोणों को उसी तरह परिभाषित किया जाता है, छोटे -180 डिग्री। उदाहरण के लिए, रोटेशन -520 डिग्री के कोण को -180, -180 और -160 डिग्री के बिंदु की निरंतर मोर्चे के रूप में व्याख्या किया जा सकता है।
संक्षेप। हमने घूर्णन के कोण को निर्धारित किया, जिसकी परिमाण डिग्री में कुछ वैध संख्या से-∞ से + π तक व्यक्त की जाती है। त्रिकोणमिति में, हम मोड़ कोणों के साथ काम करेंगे, हालांकि शब्द "मोड़" अक्सर कम हो जाता है, और वे बस "कोण" कहते हैं। इस प्रकार, त्रिकोणमिति में हम कोण कोण के साथ काम करेंगे, जिसके तहत हम मोड़ के कोणों को समझेंगे।
इस अनुच्छेद के समापन में, हम ध्यान देते हैं कि सकारात्मक दिशा में कुल कारोबार 360 डिग्री (या 2 · रेडियंस) के घूर्णन के कोण से मेल खाता है, और नकारात्मक में - -360 डिग्री (या -2) में रोटेशन का कोण) · Π खुश है)। साथ ही, यह पूर्ण क्रांतियों की एक निश्चित राशि के रूप में प्रतिनिधित्व करने के बड़े कोणों के लिए सुविधाजनक है और एक और मोड़ -180 से 180 डिग्री तक परिमाण के कोण द्वारा एक और मोड़। उदाहरण के लिए, 1,340 डिग्री के घूर्णन का कोण लें। 360 · 4 + (- 100) के रूप में 1 340 का प्रतिनिधित्व करना आसान है। यही है, रोटेशन का प्रारंभिक कोण सकारात्मक दिशा में 4 पूर्ण मोड़ और अगली बार -100 डिग्री पर बंद हो जाता है। एक और उदाहरण: रोटेशन -745 डिग्री का कोण एक दक्षिणावर्त तीर के खिलाफ दो मोड़ और -25 डिग्री के बाद के घूर्णन के रूप में व्याख्या किया जा सकता है, क्योंकि -745 \u003d (- 360) · 2 + (- 25)।
कोण पर बिंदु के चारों ओर आकार घुमाएं
बिंदु की घूर्णन की अवधारणा आसानी से बढ़ रही है कोण पर बिंदु के चारों ओर किसी भी आकार को घुमाएं (यह इस तरह की बारी के बारे में है क्योंकि इस बात के सापेक्ष बिंदु के रूप में बारी की जाती है, और आंकड़ा जो एक ही विमान में स्थित होता है, झूठ बोलता है)।
आंकड़े की बारी के तहत हम दिए गए कोण पर निर्दिष्ट बिंदु के आसपास आकृति के सभी बिंदुओं के घूर्णन को समझेंगे।
उदाहरण के तौर पर, हम निम्नलिखित कार्रवाई का एक उदाहरण देते हैं: बिंदु ओ के सापेक्ष कोण के लिए कट एबी का घूर्णन करें, यह खंड जब एक सेगमेंट में बदल जाता है तो 1 बी 1।

ग्रंथसूची।
- बीजगणित: में पढ़ता है। 9 सीएल के लिए। वातावरण Shk। / U। एन। Makaryechev, एन जी Mindyuk, के। I. Neshkov, एस बी Suvorov; ईडी। एस ए। Teleikovsky। - एम।: शिक्षा, 1 99 0.- 272 सी।: Il.- ISBN 5-09-002727-7
- Bashmakov एम I. बीजगणित और विश्लेषण शुरू करें: अध्ययन। 10-11 सीएल के लिए। वातावरण shk। - तीसरा एड। - एम।: Enlightenment, 1993. - 351 सी।: Il। - आईएसबीएन 5-09-004617-4।
- बीजगणित और विश्लेषण शुरू करना: अध्ययन। 10-11 सीएल के लिए। सामान्य शिक्षा। संस्थान / ए। एन। कोल्मोगोरोव, ए एम। अब्रामोव, यू। पी। Dudnitsyn, आदि; ईडी। ए एन। कोल्मोगोरोवा.- 14 वें एड। - एम।: Enlightenment, 2004.- 384 सी।: Il.- ISBN 5-09-013651-3।
- गुसेव वी ए, मॉर्डकोविच ए जी। गणित (तकनीकी स्कूलों में आवेदकों के लिए लाभ): अध्ययन। लाभ। - एम।; अधिक। एसएचके।, 1 9 84.-351 पी।, आईएल।