Những mặt phẳng nào được gọi là song song hãy cho ví dụ minh họa. Tính song song của các mặt phẳng: dấu hiệu, điều kiện. Các mặt phẳng song song bằng các ví dụ

Vị trí của máy bay trong không gian được xác định bởi:

• ba điểm không nằm trên một đường thẳng;
• một đoạn thẳng và một điểm lấy ngoài đường thẳng;
• hai đường thẳng cắt nhau;
• hai đường thẳng song song;
• hình phẳng.

Phù hợp với điều này, một mặt phẳng có thể được chỉ định trên sơ đồ:

• hình chiếu của ba điểm không cùng nằm trên một đường thẳng (Hình 3.1, a);
• hình chiếu của một điểm và một đoạn thẳng (Hình 3.1, b);
• hình chiếu của hai đường thẳng cắt nhau (Hình 3.1, c);
• hình chiếu của hai đường thẳng song song (Hình 3.1, d);
• một hình phẳng (Hình 3.1, e);
• dấu vết của máy bay;
• đường của hệ số góc lớn nhất của mặt phẳng.

Hình 3.1 - Các phương pháp xác định mặt phẳng

Mặt phẳng vị trí chung Là mặt phẳng không song song hoặc vuông góc với bất kỳ mặt phẳng hình chiếu nào.

Máy bay theo dõiđược gọi là đường thẳng có được do giao tuyến của một mặt phẳng đã cho với một trong các mặt phẳng hình chiếu.

Một mặt phẳng vị trí chung có thể có ba dấu vết: nằm ngang – απ 1, trán – απ 2 và Hồ sơ – απ 3, mà nó tạo thành khi nó giao với các mặt phẳng hình chiếu đã biết: nằm ngang π 1, mặt trước π 2 và mặt phẳng π 3 (Hình 3.2).

Hình 3.2 - Dấu vết của mặt phẳng ở vị trí chung

3.2. Máy bay vị trí riêng

Máy bay vị trí riêng- mặt phẳng vuông góc hoặc song song với mặt phẳng hình chiếu.

Mặt phẳng vuông góc với mặt phẳng hình chiếu gọi là hình chiếu và trên mặt phẳng hình chiếu này sẽ được hình chiếu là một đường thẳng.

Thuộc tính mặt phẳng chiếu: mọi điểm, đường thẳng, hình chiếu thuộc mặt phẳng hình chiếu đều có hình chiếu trên vết nghiêng của mặt phẳng(Hình 3.3).

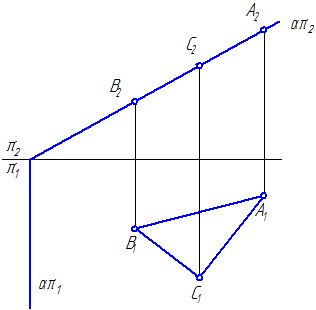
Hình 3.3 - Mặt phẳng chiếu trước, thuộc: điểm MỘT, V, VỚI; những dòng kẻ NHƯ, AB, mặt trời; mặt phẳng của tam giác ABC

Mặt phẳng chiếu trước – mặt phẳng vuông góc với mặt phẳng chiếu chính diện(Hình 3.4, a).

Mặt phẳng chiếu ngang – mặt phẳng vuông góc với mặt phẳng chiếu ngang(Hình 3.4, b).

Mặt phẳng chiếu định dạng – mặt phẳng vuông góc với mặt phẳng biên của hình chiếu.

Các mặt phẳng song song với các mặt phẳng chiếu gọi là máy bay cấp hoặc bằng cách chiếu hai lần mặt phẳng.

Mặt phẳng ngang – mặt phẳng song song với mặt phẳng chiếu chính diện(Hình 3.4, c).

Mặt phẳng ngang của mức – mặt phẳng song song với mặt phẳng chiếu ngang(Hình 3.4, d).

Mặt phẳng mức hồ sơ – mặt phẳng song song với mặt phẳng biên của hình chiếu(Hình 3.4, e).

Hình 3.4 - Sơ đồ mặt phẳng của một vị trí cụ thể

3.3. Điểm và đường thẳng trong mặt phẳng. Thuộc một điểm và một mặt phẳng thẳng

Một điểm thuộc một mặt phẳng nếu nó thuộc một đường thẳng bất kỳ nằm trong mặt phẳng này(Hình 3.5).

Đường thẳng thuộc mặt phẳng nếu nó có ít nhất hai điểm chung với mặt phẳng(Hình 3.6).

Hình 3.5 - Điểm thuộc mặt phẳng

α = m // n

D∈ n⇒ D∈ α

Hình 3.6 - Thuộc mặt phẳng thẳng

Tập thể dục

Cho một mặt phẳng, cho bởi một tứ giác (Hình 3.7, a). Cần hoàn thành hình chiếu ngang của đỉnh VỚI.

Một	b

Hình 3.7 - Giải quyết vấn đề

Giải pháp :

1. A B C D Là tứ giác phẳng xác định mặt phẳng.
2. Hãy vẽ các đường chéo trong đó AC và BD(Hình 3.7, b), là các đường thẳng cắt nhau cũng xác định cùng một mặt phẳng.
3. Theo dấu hiệu của các đường cắt nhau, chúng ta dựng một hình chiếu ngang của giao điểm của các đường này - K theo phép chiếu trực diện nổi tiếng của cô ấy: MỘT 2 C 2 ∩ B 2 D 2 = K 2 .
4. Khôi phục đường nối hình chiếu về giao điểm với hình chiếu ngang của đường thẳng BD: trên hình chiếu của đường chéo B 1 D 1 tòa nhà ĐẾN 1 .
5. Bên kia MỘT 1 ĐẾN 1 chúng tôi vẽ một hình chiếu của đường chéo MỘT 1 VỚI 1 .
6. Điểm VỚI 1, chúng tôi thu được bằng đường của kết nối hình chiếu cho đến khi nó giao với hình chiếu ngang của đường chéo mở rộng MỘT 1 ĐẾN 1 .

3.4. Các đường chính của máy bay

Trong một mặt phẳng, bạn có thể dựng vô số đường thẳng, nhưng có những đường đặc biệt nằm trong mặt phẳng, được gọi là các đường chính của máy bay (Hình 3.8 - 3.11).

Cấp độ trực tiếp hoặc song song với mặt phẳng gọi là đường thẳng nằm trong một mặt phẳng cho trước và song song với một trong các mặt phẳng hình chiếu.

Ngang hoặc đường ngang của mức h(song song thứ nhất) là một đường thẳng nằm trong một mặt phẳng cho trước và song song với mặt phẳng chiếu ngang (π 1)(Hình 3.8, a; 3.9).

Mặt trước hoặc đường thẳng phía trước f(vĩ tuyến thứ hai) là một đường thẳng nằm trong một mặt phẳng cho trước và song song với mặt phẳng chính diện của hình chiếu (π 2)(Hình 3.8, b; 3.10).

Hồ sơ đường thẳng của mức độ P(vĩ tuyến thứ ba) là một đường thẳng nằm trong mặt phẳng này và song song với mặt phẳng hình chiếu của hình chiếu (π 3)(Hình 3.8, c; 3.11).

Hình 3.8 a - Đường ngang của mức trong mặt phẳng xác định bởi tam giác

Hình 3.8 b - Đường giới hạn của mức trong mặt phẳng xác định bởi tam giác

Hình 3.8 c - Đường giới hạn của mức trong mặt phẳng xác định bởi tam giác

Hình 3.9 - Đường ngang của mức trong mặt phẳng được xác định bởi các dấu vết

Hình 3.10 - Đường trực diện của mức trong mặt phẳng được chỉ định bởi các đường

Hình 3.11 - Đường biên dạng của mức trong mặt phẳng được chỉ định bởi các đường

3.5. Vị trí tương đối của đường thẳng và mặt phẳng

Một đường thẳng đối với một mặt phẳng đã cho có thể song song và có thể có một điểm chung với nó, nghĩa là cắt nhau.

3.5.1. Tính song song của một mặt phẳng thẳng

Song song với một mặt phẳng thẳng: một đường thẳng song song với một mặt phẳng nếu nó song song với bất kỳ đường thẳng nào thuộc mặt phẳng này(Hình 3.12).

Hình 3.12 - Phép song song của một mặt phẳng thẳng

3.5.2. Giao điểm của đường thẳng với mặt phẳng

Để xây dựng giao điểm của đường thẳng với mặt phẳng ở vị trí chung (Hình 3.13), bạn phải:

1. Kết luận một đường thẳng Một vào mặt phẳng phụ β (mặt phẳng của vị trí cụ thể nên được chọn làm mặt phẳng phụ);
2. Tìm giao tuyến của mặt phẳng phụ β với mặt phẳng α cho trước;
3. Tìm giao điểm của một đường thẳng cho trước Một với đường giao tuyến của các mặt phẳng MN.

Hình 3.13 - Dựng giao điểm của đường thẳng với mặt phẳng

Tập thể dục

Đặt trước: thẳng ABở vị trí chung, mặt phẳng σ⊥π 1. (Hình 3.14). Vẽ đường giao nhau AB với mặt phẳng σ.

Giải pháp :

1. Mặt phẳng σ là hình chiếu theo phương ngang nên hình chiếu ngang của mặt phẳng σ là đường thẳng σ 1 (vết ngang của mặt phẳng);
2. Chấm ĐẾN phải thuộc về trực tiếp AB ⇒ ĐẾN 1 ∈MỘT 1 V 1 và một mặt phẳng cho trước σ ⇒ ĐẾN 1 ∈σ 1, do đó ĐẾN 1 là giao điểm của các phép chiếu MỘT 1 V 1 và σ 1;
3. Hình chiếu trực diện của một điểm ĐẾN chúng tôi tìm thấy thông qua dòng giao tiếp chiếu: ĐẾN 2 ∈MỘT 2 V 2 .

Hình 3.14 - Giao điểm của một đường thẳng ở vị trí chung với mặt phẳng có vị trí cụ thể

Tập thể dục

Cho: mặt phẳng σ = Δ ABC- vị trí chung, thẳng EF(Hình 3.15).

Yêu cầu xây dựng giao điểm của một đường thẳng EF với mặt phẳng σ.

Một	b

Hình 3.15 - Giao điểm của đường thẳng với mặt phẳng

1. Hãy để chúng tôi kết luận một đường thẳng EF vào mặt phẳng phụ, vì chúng ta sẽ sử dụng mặt phẳng chiếu nằm ngang α (Hình 3.15, a);
2. Nếu α⊥π 1 thì trên mặt phẳng hình chiếu π 1 hình chiếu mặt phẳng α thành một đường thẳng (vết nằm ngang của mặt phẳng απ 1 hoặc α 1) trùng với E 1 F 1 ;
3. Ta hãy tìm giao tuyến (1-2) của mặt phẳng hình chiếu α với mặt phẳng σ (sẽ xét lời giải của một bài toán tương tự);
4. Thẳng (1-2) và cho thẳng EF nằm trong cùng một mặt phẳng α và cắt nhau tại điểm K.

Thuật toán để giải quyết vấn đề (Hình 3.15, b):

Bên kia EF chúng ta vẽ một mặt phẳng phụ α:

3.6. Xác định khả năng hiển thị bằng phương pháp điểm cạnh tranh

Khi đánh giá vị trí của một đoạn thẳng đã cho, cần phải xác định - điểm của đoạn thẳng nằm gần chúng ta hơn (xa hơn) đối với chúng ta, đối với người quan sát, khi nhìn vào mặt phẳng của các hình chiếu π 1 hoặc π 2 .

Các điểm thuộc các đối tượng khác nhau và trên một trong các mặt phẳng chiếu, các hình chiếu của chúng trùng nhau (nghĩa là hai điểm được chiếu thành một) được gọi là cạnh nhau trên mặt phẳng chiếu này.

Cần xác định riêng khả năng hiển thị trên từng mặt phẳng hình chiếu.

Khả năng hiển thị ở góc π 2 (Hình 3.15)

Chúng ta hãy chọn các điểm cạnh tranh trên π 2 - điểm 3 và 4. Cho điểm 3∈ ВС∈σ, điểm 4∈ EF.

Để xác định tầm nhìn của các điểm trên mặt phẳng hình chiếu π 2, cần xác định vị trí của các điểm này trên mặt phẳng hình chiếu ngang khi nhìn góc π 2.

Hướng nhìn về góc π 2 được biểu diễn bằng một mũi tên.

Từ hình chiếu ngang của điểm 3 và điểm 4 khi nhìn một góc π 2 có thể thấy điểm 4 1 nằm gần người quan sát hơn 3 1.

4 1 ∈E 1 F 1 ⇒ 4∈EF⇒ điểm 4 sẽ hiển thị trên π 2, nằm trên đường thẳng EF do đó đường thẳng EF trong phân đoạn của các điểm cạnh tranh được coi là nằm ở phía trước của mặt phẳng σ và sẽ hiển thị cho đến điểm K

Khả năng hiển thị ở π 1

Để xác định khả năng hiển thị, chúng tôi chọn các điểm cạnh tranh trên π 1 - điểm 2 và 5.

Để xác định tầm nhìn của các điểm trên mặt phẳng hình chiếu π 1, cần xác định vị trí của các điểm này trên mặt phẳng chính diện của hình chiếu khi nhìn góc π 1.

Hướng nhìn đến góc π 1 được biểu diễn bằng một mũi tên.

Từ hình chiếu trực diện của điểm 2 và điểm 5 khi nhìn một góc π 1 có thể thấy điểm 2 2 nằm gần người quan sát hơn 5 2.

2 1 ∈MỘT 2 V 2 ⇒ 2∈AB⇒ điểm 2 sẽ hiển thị trên π 1, nằm trên đường thẳng AB do đó đường thẳng EF trên phân đoạn của các điểm cạnh tranh được coi là nằm dưới mặt phẳng σ và sẽ vô hình cho đến điểm K- Giao điểm của đường thẳng với mặt phẳng σ.

Điểm hiển thị của hai điểm cạnh tranh sẽ là điểm có tọa độ "Z" hoặc (các) "Y" lớn hơn.

3.7. Tính vuông góc với một mặt phẳng thẳng

Tính vuông góc với một mặt phẳng thẳng: Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng này.

Một	b

Hình 3.16 - Xác định một đường thẳng vuông góc với mặt phẳng

Định lý. Nếu đường thẳng vuông góc với mặt phẳng thì trên sơ đồ: hình chiếu ngang của đường thẳng vuông góc với hình chiếu ngang của mặt phẳng nằm ngang và hình chiếu chính diện của đường thẳng vuông góc với hình chiếu chính diện của (Hình 3.16, b)

Định lý được chứng minh thông qua định lý về hình chiếu của góc vuông trong một trường hợp cụ thể.

Nếu mặt phẳng được xác định bằng các vết, thì các hình chiếu của đường thẳng vuông góc với mặt phẳng sẽ vuông góc với các vết tương ứng của mặt phẳng (Hình 3.16, a).

Hãy để nó được thẳng P vuông góc với mặt phẳng σ = Δ ABC và đi qua điểm K.

1. Ta dựng phương ngang và mặt trước trong mặt phẳng σ = Δ ABC : A-1∈σ; A-1// π 1; C-2∈σ; C-2// π 2.
2. Phục hồi từ điểm K vuông góc với một mặt phẳng cho trước: p 1⊥h 1 và p 2⊥f 2, hoặc là p 1⊥απ 1 và p 2⊥απ 2

3.8. Vị trí tương hỗ của hai mặt phẳng

3.8.1. Song song của các mặt phẳng

Hai mặt phẳng có thể song song và cắt nhau.

Tính song song của hai mặt phẳng: hai mặt phẳng song song với nhau nếu hai đường thẳng chéo nhau của một mặt phẳng tương ứng song song với hai đường thẳng chéo nhau của một mặt phẳng khác.

Tập thể dục

Một mặt phẳng ở vị trí tổng quát α = Δ ABC và chỉ F∉α (Hình 3.17).

Xuyên suốt F vẽ mặt phẳng β song song với mặt phẳng α.

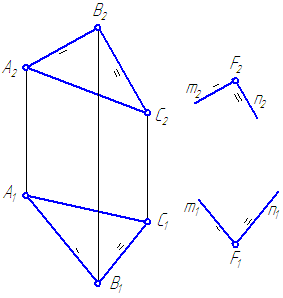
Hình 3.17 - Dựng một mặt phẳng song song với một mặt phẳng cho trước

Giải pháp :

Là các đường thẳng cắt nhau của mặt phẳng α, ta lấy các cạnh của tam giác AB và BC làm ví dụ.

1. Xuyên suốt F chúng tôi vẽ một đường thẳng m song song, ví dụ, AB.
2. Xuyên suốt F hoặc thông qua bất kỳ điểm nào thuộc về m, chúng tôi vẽ một đường thẳng n song song, ví dụ, mặt trời, và m∩n = F.
3. β = m∩n và β // α theo định nghĩa.

3.8.2. Giao điểm của các mặt phẳng

Kết quả giao tuyến của 2 mặt phẳng là một đường thẳng. Bất kỳ đường thẳng nào trên mặt phẳng hoặc trong không gian đều có thể được xác định duy nhất bởi hai điểm. Do đó, để dựng đường giao tuyến của hai mặt phẳng, bạn nên tìm hai điểm chung của cả hai mặt phẳng rồi nối chúng lại.

Hãy xem xét các ví dụ về giao tuyến của hai mặt phẳng với các cách giao của chúng khác nhau: bằng dấu vết; ba điểm không nằm trên một đường thẳng; các đường thẳng song song; các đường thẳng cắt nhau, v.v.

Tập thể dục

Hai mặt phẳng α và β được xác định bởi các vết (Hình 3.18). Dựng đường giao tuyến của các mặt phẳng.

Hình 3.18 - Giao điểm của các mặt phẳng ở vị trí chung, được xác định bằng dấu vết

Trình tự xây dựng đường giao tuyến của các mặt phẳng:

1. Tìm giao điểm của các vết ngang là một điểm M(dự đoán của nó M 1 và M 2, trong khi M 1 = M từ M - một điểm của một vị trí cụ thể thuộc mặt phẳng π 1).
2. Tìm giao điểm của các rãnh phía trước là điểm n(dự đoán của nó n 1 và n 2, trong khi n 2 = n từ N - một điểm của một vị trí cụ thể thuộc mặt phẳng π 2).
3. Dựng đường giao tuyến của các mặt phẳng bằng cách nối các hình chiếu giống nhau của các điểm thu được: M 1 n 1 và M 2 n 2 .

Mn- đường giao tuyến của các mặt phẳng.

Tập thể dục

Mặt phẳng σ = Δ ABC, mặt phẳng α - hình chiếu theo phương ngang (α⊥π 1) ⇒α 1 - vết ngang của mặt phẳng (Hình 3.19).

Dựng đường giao tuyến của các mặt phẳng này.

Giải pháp :

Vì mặt phẳng α cắt các cạnh AB và NHƯ Tam giác ABC, sau đó là các điểm giao nhau K và L của những mặt này với mặt phẳng α là chung cho cả hai mặt phẳng đã cho, điều này sẽ làm cho nó có thể, bằng cách nối chúng, để tìm đường giao tuyến cần thiết.

Có thể tìm điểm là giao điểm của đường thẳng với mặt phẳng hình chiếu: ta tìm hình chiếu ngang của điểm K và L, đó là K 1 và L 1, tại giao điểm của vết ngang (α 1) của một mặt phẳng α cho trước với hình chiếu nằm ngang của các cạnh Δ ABC: MỘT 1 V 1 và MỘT 1 C một . Sau đó, bằng cách sử dụng các đường giao tiếp của phép chiếu, chúng tôi tìm thấy các hình chiếu phía trước của những điểm này K 2 và L 2 về hình chiếu trực diện của các đường thẳng AB và NHƯ... Hãy kết nối các phép chiếu cùng tên: K 1 và L 1 ; K 2 và L 2. Vẽ đường giao tuyến của các mặt phẳng đã cho.

Thuật toán để giải quyết vấn đề:

KL- đường giao nhau Δ ABC và σ (α∩σ = KL).

Hình 3.19 - Giao điểm của các mặt phẳng nói chung và vị trí riêng

Tập thể dục

Mặt phẳng α = m // n và mặt phẳng β = Δ ABC(Hình 3.20).

Dựng đường giao tuyến của các mặt phẳng đã cho.

Giải pháp :

1. Để tìm điểm chung của cả hai mặt phẳng xác định và xác định đường giao tuyến của hai mặt phẳng α và β, cần sử dụng các mặt phẳng phụ của một vị trí cụ thể.
2. Như các mặt phẳng như vậy, chúng ta chọn hai mặt phẳng phụ của một vị trí cụ thể, ví dụ: σ // τ; σ⊥π 2; τ⊥π 2.
3. Các mặt phẳng mới được giới thiệu cắt mỗi mặt phẳng α và β đã cho dọc theo các đường thẳng song song với nhau, vì σ // τ:

- kết quả của giao tuyến của các mặt phẳng α, σ và τ là các đường thẳng (4-5) và (6-7);

- kết quả của giao tuyến của các mặt phẳng β, σ và τ là các đường thẳng (3-2) và (1-8).

1. Các đường thẳng (4-5) và (3-2) nằm trong mặt phẳng σ; điểm giao nhau của họ M nằm đồng thời trong hai mặt phẳng α và β, nghĩa là, trên đường giao tuyến của các mặt phẳng này;
2. Tương tự, chúng tôi tìm thấy điểm n chung cho các mặt phẳng α và β.
3. Bằng cách kết nối các dấu chấm M và n, chúng ta dựng một đường giao tuyến của hai mặt phẳng α và β.

Hình 3.20 - Giao điểm của hai mặt phẳng ở vị trí chung (trường hợp chung)

Thuật toán để giải quyết vấn đề:

Tập thể dục

Các mặt phẳng α = Δ ABC và β = Một//b... Dựng đường giao tuyến của các mặt phẳng đã cho (Hình 3.21).

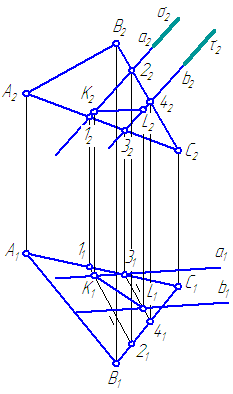
Hình 3.21 Giải bài toán về giao tuyến của các mặt phẳng

Giải pháp :

Hãy sử dụng các mặt phẳng cắt phụ của vị trí cụ thể. Hãy giới thiệu chúng theo cách để giảm số lượng công trình. Ví dụ, chúng tôi giới thiệu mặt phẳng σ⊥π 2, bao quanh đường thẳng Một vào mặt phẳng phụ σ (σ∈ Một). Mặt phẳng σ cắt mặt phẳng α theo đường thẳng (1-2) và σ∩β = Một... Do đó (1-2) ∩ Một=K.

Chấm ĐẾN thuộc cả hai mặt phẳng α và β.

Do đó điểm K, là một trong những điểm cần tìm mà đường giao tuyến của hai mặt phẳng α và β đã cho đi qua.

Để tìm điểm thứ hai thuộc giao điểm của α và β, ta kết luận đường b vào mặt phẳng phụ τ⊥π 2 (τ∈ b).

Bằng cách kết nối các dấu chấm K và L, ta thu được đường giao tuyến của hai mặt phẳng α và β.

3.8.3. Các mặt phẳng vuông góc với nhau

Các máy bay vuông góc với nhau nếu một trong số chúng đi qua phương vuông góc với máy bay kia.

Tập thể dục

Một mặt phẳng σ⊥π 2 và một đường thẳng ở vị trí chung cho trước - DE(Hình 3.22)

Nó được yêu cầu để xây dựng thông qua DE máy bay τ⊥σ.

Giải pháp .

Hãy vẽ một đường vuông góc đĩa CD lên máy bay σ - C 2 D 2 ⊥σ 2 (dựa trên).

Hình 3.22 - Dựng mặt phẳng vuông góc với mặt phẳng cho trước

Theo định lý hình chiếu góc vuông C 1 D 1 phải song song với trục hình chiếu. Giao nhau giữa các đường thẳng CD∩DE xác định mặt phẳng τ. Vì vậy τ⊥σ.

Suy luận tương tự trong trường hợp mặt phẳng ở vị trí tổng quát.

Tập thể dục

Mặt phẳng α = Δ ABC và chỉ K ngoài mặt phẳng α.

Yêu cầu dựng mặt phẳng β⊥α đi qua điểm K.

Thuật toán để giải quyết(Hình 3.23):

1. Hãy xây dựng một chiều ngang h và trán f trong một mặt phẳng cho trước α = Δ ABC;
2. Xuyên suốt K vẽ một đường vuông góc bđến mặt phẳng α (dọc theo định lý vuông góc mặt phẳng: nếu đường thẳng vuông góc với mặt phẳng thì hình chiếu của nó vuông góc với hình chiếu xiên của phương ngang và phương thẳng đứng, nằm trong mặt phẳng:b 2⊥f 2; b 1⊥h 1;
3. Chúng ta xác định mặt phẳng β theo bất kỳ cách nào, ví dụ, β = a∩b, do đó, mặt phẳng vuông góc với mặt phẳng đã cho được xây dựng: α⊥β.

Hình 3.23 - Dựng mặt phẳng vuông góc với Δ cho trước ABC

3.9. Nhiệm vụ cho giải pháp độc lập

1. Mặt phẳng α = m//n(Hình 3.24). Được biết rằng K∈α.

Xây dựng hình chiếu trực diện của một điểm ĐẾN.

Hình 3.24

2. Xây dựng các dấu vết của một đoạn thẳng được xác định bởi một đoạn CB, và xác định các góc phần tư mà nó đi qua (Hình 3.25).

Hình 3.25

3. Dựng hình chiếu của hình vuông thuộc mặt phẳng α⊥π 2, nếu đường chéo của nó MN// π 2 (Hình 3.26).

Hình 3.26

4. Dựng hình chữ nhật A B C D với một mặt lớn hơn mặt trời trên một đường thẳng m, tiếp tục với điều kiện tỷ số các cạnh của nó bằng 2 (Hình 3.27).

Hình 3.27

5. Mặt phẳng α = Một//b(Hình 3.28). Dựng mặt phẳng β song song với mặt phẳng α và cách nó một đoạn 20 mm.

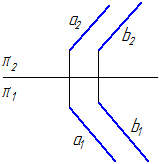
Hình 3.28

6. Mặt phẳng α = ∆ ABC và chỉ D D mặt phẳng β⊥α và β⊥π 1.

7. Mặt phẳng α = ∆ ABC và chỉ D ngoài máy bay. Xây dựng thông qua điểm D thẳng DE// α và DE// π 1.

Tính song song của các mặt phẳng. Nếu hai đường thẳng chéo nhau của một mặt phẳng lần lượt song song với hai đường thẳng chéo nhau của một mặt phẳng khác thì hai mặt phẳng này song song với nhau.
Bằng chứng. Cho phép Một và b- dữ liệu máy bay, một 1 và một 2- đường thẳng trong mặt phẳng Một giao nhau tại điểm A, b 1 và b 2 tương ứng song song với chúng các đường thẳng trong mặt phẳng b... Chúng ta hãy giả định rằng các máy bay Một và b không song song, tức là chúng cắt nhau dọc theo một số đường thẳng Với... Thẳng Một 1 song song với một đường thẳng b 1, có nghĩa là nó song song với mặt phẳng b(dấu hiệu nhận biết độ song song của đường thẳng và mặt phẳng). Thẳng Một 2 song song với một đường thẳng b 2, thì nó song song với mặt phẳng b(dấu hiệu nhận biết độ song song của đường thẳng và mặt phẳng). Thẳng Với thuộc về máy bay Một, thì ít nhất một trong các đường thẳng một 1 hoặc là một 2 băng qua đường thẳng Với, nghĩa là nó có một điểm chung với nó. Nhưng thẳng Với cũng thuộc về máy bay b do đó, băng qua đường thẳng Với, thẳng một 1 hoặc là một 2 băng qua máy bay b, không thể được, vì thẳng một 1 và một 2 song song với mặt phẳng b... Từ đó các máy bay Một và b không cắt nhau, tức là chúng song song.

Định lý 1 ... Nếu hai mặt phẳng song song cắt nhau một phần ba thì các giao tuyến song song.
Bằng chứng. Cho phép Một và b- mặt phẳng song song, và g - mặt phẳng giao nhau giữa chúng. Máy bay Một vượt qua máy bay g trong một đường thẳng Một. Máy bay b vượt qua máy bay g trong một đường thẳng b.Đường giao nhau Một và b nằm trong cùng một mặt phẳng g và do đó có thể là hai đường thẳng cắt nhau hoặc song song. Nhưng, thuộc hai mặt phẳng song song thì chúng không thể có điểm chung. Do đó, chúng song song với nhau.

Định lý 2. Các đoạn thẳng song song giữa hai mặt phẳng song song bằng nhau.
Bằng chứng. Cho phép Một và b- mặt phẳng song song, và Một và b- các đường thẳng song song cắt ngang chúng. Qua thẳng Một và b sẽ thực hiện chiếc máy bay g (những đường thẳng này song song với nhau, vì vậy xác định một mặt phẳng và chỉ một). Máy bay Một vượt qua máy bay g trên đường thẳng AB . Máy bay b vượt qua máy bay g dọc theo đường thẳng SD. Theo định lý trước, đường thẳng Với song song với đường thẳng d... Trực tiếp Một,b, AB và SD thuộc mặt phẳng g Tứ giác giới hạn bởi các đường thẳng này là một hình bình hành (các cạnh đối diện của nó song song). Và vì đây là hình bình hành nên các cạnh đối diện của nó bằng nhau, tức là HELL = BC

Xét quan hệ của phép song song phẳng, các tính chất và ứng dụng của nó.

Mô tả trực quan về vị trí của hai

Planes cung cấp mô hình bằng cách sử dụng các mặt phẳng của các bề mặt của các bức tường liền kề, trần và sàn của căn phòng, giường tầng, hai tờ giấy được liên kết

pháp sư, v.v. (Hình 242-244).

Mặc dù có vô số lựa chọn cho vị trí tương đối của các mặt phẳng khác nhau, để thiết lập và các đặc điểm của các góc và khoảng cách sẽ được đo sau này, trước tiên chúng ta dựa trên những lựa chọn mà phân loại (cũng như các đường với mặt phẳng) dựa trên số điểm chung của chúng.

1. Hai mặt phẳng có ít nhất ba điểm chung không nằm trên một đường thẳng. Các mặt phẳng như vậy trùng nhau (Tiên đề C 2, Phần 7).

2. Điểm chung của hai mặt phẳng cùng nằm trên một đường thẳng là giao tuyến của hai mặt phẳng này (Tiên đề C 3, §7). Các mặt phẳng như vậy cắt nhau.

3. Hai mặt phẳng không có điểm chung.

V trong trường hợp này chúng được gọi là song song

Hai mặt phẳng được cho là song song nếu chúng không có điểm chung.

Tính song song của các mặt phẳng được biểu thị bằng dấu ||: α || β.

Như mọi khi, khi các khái niệm hình học được giới thiệu,

có một vấn đề về sự tồn tại của họ. Sự tồn tại của giao nhau

máy bay là một tính năng đặc trưng của không gian,

và chúng tôi đã sử dụng nó nhiều lần. Ít rõ ràng hơn

Các mặt phẳng song song tồn tại. Không có

nghi ngờ rằng, ví dụ, các mặt phẳng của các mặt đối diện

các hình lập phương của cô ấy là song song, tức là, không cắt nhau. Nhưng trực tiếp

Nó chắc chắn là không thể thiết lập theo định nghĩa. Để có một giải pháp

câu hỏi được đặt ra, cũng như các vấn đề khác liên quan đến

độ song song của các mặt phẳng thì cần phải có dấu song song.

Để tìm kiếm một tính năng, bạn nên xem xét máy bay,

"Dệt" từ các đường thẳng. Rõ ràng, mỗi dòng là một trong những

mặt phẳng song song phải song song với mặt khác.

Nếu không, các mặt phẳng sẽ có một điểm chung. Hợp lý

là phương song song của mặt phẳng β với một đường thẳng của mặt phẳng α

sao cho hai mặt phẳng α và β song song? Vô điều kiện

nhưng, không (biện minh cho nó!). Kinh nghiệm thực tế cho thấy rằng

hai đường thẳng cắt nhau như vậy là đủ. Bảo vệ

một nền tảng song song với mặt đất trên cột buồm, chỉ cần đặt nó

song song với mặt phẳng thứ hai thì các mặt phẳng này song song với nhau.

 Để hai đường thẳng chéo nhau a và b của mặt phẳng α song song với mặt phẳng β. Hãy chứng minh rằng các mặt phẳng α và β là song song với nhau bằng cách mâu thuẫn. Để làm điều này, giả sử rằng các mặt phẳng α và β cắt nhau dọc theo một đường thẳng

t (Hình 246). Các dòng a và b không thể cắt dòng m theo điều kiện. Tuy nhiên, trong mặt phẳng α qua một điểm kẻ hai đường thẳng không cắt với đường thẳng m, tức là song song với nó. Mâu thuẫn này

và hoàn thành việc chứng minh định lý.

Dấu hiệu của độ song song mặt phẳng được sử dụng để bố trí ngang của kết cấu phẳng (tấm bê tông, sàn, đĩa thiết bị đo lường, vv) sử dụng hai mức đặt trong mặt phẳng của kết cấu trên các đường thẳng cắt nhau. Dựa trên đặc điểm này, bạn có thể dựng một mặt phẳng song song với mặt phẳng này.

Bài toán 1. Qua một điểm nằm ngoài mặt phẳng đã cho, kẻ một mặt phẳng song song với mặt phẳng đã cho.

 Cho mặt phẳng β và điểm M nằm ngoài mặt phẳng (Hình 247, a). Vẽ qua điểm M hai đường thẳng chéo nhau a và b song song với mặt phẳng β. Để làm điều này, bạn cần phải lấy trong mặt phẳng β hai đường thẳng cắt nhau c và d (Hình. 247, b). Khi đó qua điểm M kẻ các đường thẳng a, b lần lượt song song với các đường thẳng c, d.

nhưng (Hình. 247, c).

Các đường giao nhau a và b song song với mặt phẳng β, theo tiêu chuẩn là tính song song của đường thẳng và mặt phẳng (Định lý 1 §11). Chúng xác định duy nhất mặt phẳng α. Theo tiêu chuẩn đã được chứng minh, α || β.

Ví dụ 1. Cho hình lập phương ABCDA 1 B 1 C 1 D 1, các điểm M, N, P lần lượt là trung điểm của các cạnh BC, B 1 C 1, A 1 D 1. Lập vị trí tương đối của các mặt phẳng: 1) ABB 1 và PNM; 2) NMA và A 1 C 1 C; 3) A 1 NM

và PC 1 C; 4) MAD 1 và DB 1 C.

 1) Các mặt phẳng ABB 1 và PNM (Hình 248) song song, theo tính song song của các mặt phẳng (Định lý 1). Thật vậy, các đường thẳng PN và NM cắt nhau và song song với mặt phẳng ABB 1, trên cơ sở tính song song của đường thẳng và mặt phẳng (Định lý 1 §11), vì các đoạn thẳng PN và NM nối các trung điểm của đối diện. các cạnh của hình vuông, do đó chúng song song với các cạnh của hình vuông:

РN || A 1 B 1, NM || B 1 B.

2) Các mặt phẳng NMA và A 1 C 1 C cắt nhau theo đường thẳng AA 1 (Hình 249). Thật vậy, các đường thẳng AA 1 và СC 1 là song song, theo tiêu chuẩn về tính song song của các đường thẳng (AA 1 || ВB 1, ВB 1 || СC 1). Do đó, đường thẳng AA 1 nằm trong mặt phẳng A 1 C 1 C. Việc thuộc đường thẳng AA 1 với mặt phẳng NMA cũng được chứng minh tương tự.

3) Các mặt phẳng A 1 NM và PC 1 C (Hình 250) là song song, trên cơ sở tính song song của các mặt phẳng. Thật vậy, NM || C 1 C. Do đó, đường thẳng NM song song với mặt phẳng PC 1 C. Đoạn thẳng PC 1 và A 1 N cũng song song với nhau do tứ giác PC 1 NA 1 là hình bình hành (A 1 P || NC 1, A 1 P = NC 1). Do đó, đường thẳng A 1 N song song với mặt phẳng PC 1 C. Đường thẳng A 1 N và NM cắt nhau.

4) Các mặt phẳng MAD 1 và DB 1 C cắt nhau (hình 251). Mặc dù không dễ dàng để xây dựng đường giao nhau của chúng, nhưng không khó để chỉ ra một điểm của đường này. Thật vậy, các đường thẳng A 1 D và B 1 C song song với nhau vì tứ giác A 1 B 1 CD là hình bình hành (A 1 B 1 = AB = CD, A 1 B 1 || AB, AB || CD). Do đó, đường thẳng A 1 D thuộc mặt phẳng DB 1 C. Các đường thẳng A 1 D và AD 1 gặp nhau tại một điểm chung của hai mặt phẳng MAD 1 và DB 1 C.

Nếu hai đường thẳng chéo nhau của một mặt phẳng lần lượt song song với hai đường thẳng của mặt phẳng khác thì hai mặt phẳng này song song với nhau.

Sử dụng tiêu chuẩn về tính song song của đường thẳng và mặt phẳng (Định lý 1 §11), ta dễ dàng xác định được điều kiện của Định lý 1 từ điều kiện của Định lý 1. ′.

Câu hỏi tự nhiên nảy sinh về tính duy nhất của công trình được đưa ra trong Bài toán 1. Vì chúng ta sẽ phải sử dụng thuộc tính này nhiều lần, chúng ta sẽ tách nó ra thành một định lý riêng. Tuy nhiên, chúng ta hãy xem xét một tuyên bố khác trước.

Định lý 2 (về giao tuyến của hai mặt phẳng song song thứ ba).

Nếu hai mặt phẳng song song cắt mặt phẳng thứ ba thì đường giao tuyến của hai mặt phẳng đó song song với nhau.

 Cho các mặt phẳng song song α, β và một mặt phẳng γ cắt chúng (Hình 252). Hãy đánh dấu các đường giao nhau

thông qua a và b. Các đường thẳng này nằm trong mặt phẳng γ và không cắt nhau, vì hai mặt phẳng α và β không có điểm chung. Do đó, trực tiếp

a và b song song với nhau.

Định lý 3 (về sự tồn tại và tính duy nhất của mặt phẳng song song với một mặt phẳng cho trước).

Qua một điểm nằm bên ngoài mặt phẳng đã cho, bạn có thể vẽ một mặt phẳng song song với mặt phẳng đã cho.

 Việc xây dựng một mặt phẳng như vậy đã được thực hiện trong Bài toán 1. Tính độc đáo của việc xây dựng sẽ được chứng minh bằng sự mâu thuẫn. Giả sử rằng hai mặt phẳng khác nhau α và γ được vẽ qua điểm M,

mặt phẳng song song β (Hình 253), và đường thẳng t là giao tuyến của chúng. Vẽ qua điểm M mặt phẳng δ cắt với đường thẳng

m và mặt phẳng β (làm thế nào điều này có thể được thực hiện?). Chúng tôi ký hiệu là a và b

đường giao tuyến của mặt phẳng δ với mặt phẳng α và γ, và qua c - đường giao tuyến của mặt phẳng δ và β (Hình 253). Theo Định lý 2, và || Với

và b || Với. Đó là, trong mặt phẳng δ qua

điểm M cách hai đường thẳng song song với đường thẳng c. Sự mâu thuẫn chỉ ra tính không chính xác của giả định.

Tỷ lệ song song mặt phẳng có một số thuộc tính có giá trị tương tự về độ phẳng.

Định lý 4 (về các đoạn đường thẳng song song giữa các mặt phẳng song song).

Các đoạn thẳng song song, cắt bởi hai mặt phẳng song song thì bằng nhau.

 Cho hai mặt phẳng song song α và β và các đoạn thẳng AB

và CD của các đường thẳng song song a và d, cắt bởi các mặt phẳng này (Hình 254, a). Chúng ta hãy vẽ mặt phẳng γ qua các đường thẳng a và d (Hình 254, b). Nó cắt các mặt phẳng α và β dọc theo các đường thẳng AC và BD, theo Định lý 2, chúng song song với nhau. Do đó tứ giác ABCD là hình bình hành, các cạnh đối diện AC và BD bằng nhau.

Theo tính chất trên, nếu chúng ta hoãn từ tất cả các điểm của máy bay

về một phía của mặt phẳng các đoạn thẳng song song có cùng độ dài thì cuối các đoạn này tạo thành hai mặt phẳng song song. Dựa trên đặc tính này, việc xây dựng một ống song song được dựa trên việc sử dụng sự lắng đọng của các phân đoạn (Hình. 255).

Định lý 5 (về tính chuyển của quan hệ song song của các mặt phẳng).

Nếu mỗi trong hai mặt phẳng song song với mặt phẳng thứ ba thì hai mặt phẳng này song song với nhau.

 Cho hai mặt phẳng α và β song song với mặt phẳng γ. Hãy để chúng tôi giả định rằng

α và β không song song. Khi đó hai mặt phẳng α và β có điểm chung và hai mặt phẳng khác song song với mặt phẳng γ đi qua điểm này mâu thuẫn với Định lý 3. Do đó, hai mặt phẳng α và β không có điểm chung tức là chúng song song.

Định lý 5 là một tiêu chí khác cho tính song song của các mặt phẳng. Nó được sử dụng rộng rãi cả trong hình học và thực tế. Ví dụ, trong một tòa nhà nhiều tầng, sự song song của mặt bằng sàn và trần ở mỗi tầng đảm bảo sự song song của chúng trên các tầng khác nhau.

Bài toán 2. Chứng minh rằng nếu đường thẳng a cắt mặt phẳng α thì nó cũng cắt mỗi mặt phẳng song song với mặt phẳng α.

 Cho hai mặt phẳng α và β song song và đường thẳng a cắt mặt phẳng α tại điểm A. Hãy chứng minh rằng nó cũng cắt mặt phẳng

β. Hãy nói rằng nó không phải là. Khi đó đường thẳng a song song với mặt phẳng β. Chúng ta hãy vẽ mặt phẳng γ qua đường thẳng a và một điểm tùy ý của mặt phẳng β (Hình 256).

Mặt phẳng này cắt các mặt phẳng song song α và β dọc theo các đường thẳng b và c. Co-

theo Định lý 2, b || c, nghĩa là trong mặt phẳng γ qua điểm A có hai đường thẳng a và b cùng song song với đường thẳng c ... Sự mâu thuẫn này chứng tỏ nhận định.

Hãy tự chứng minh rằng nếu mặt phẳng α cắt mặt phẳng β thì nó cũng cắt mọi mặt phẳng song song với mặt phẳng β.

Ví dụ 2. Trong tứ diện ABCD, các điểm K, F, E lần lượt là trung điểm của các cạnh DA, DC, DB, M và P lần lượt là tâm của các mặt ABD và BCD.

1) Lập vị trí tương đối của hai mặt phẳng KEF và ABC;

DEF và ABC.

2) Dựng đường giao tuyến của hai mặt phẳng AFB và KEC.

3) Tìm thiết diện của tứ diện bởi mặt phẳng song song với mặt phẳng ABD và đi qua điểm P, nếu tất cả các cạnh của tứ diện đều bằng a.

 Hãy dựng một hình tương ứng với điều kiện (hình 257, a). 1) Hai mặt phẳng KEF và ABC song song, theo tính chất song song của mặt phẳng (Định lí 1 '): các đường thẳng cắt nhau KE và KF của mặt phẳng KEF song song với các đường thẳng chéo nhau AB và AC của mặt phẳng ABC (trên chúng các dòng giữa của tương ứng

Hình tam giác).

Các mặt phẳng DEF và ABC cắt nhau dọc theo đường thẳng BC, vì đường thẳng BC thuộc cả hai mặt phẳng và chúng không thể trùng nhau - các điểm A, B, C, D không nằm trong cùng một mặt phẳng.

2) Mặt phẳng AFB cắt với mặt phẳng KEC theo đường thẳng chứa điểm P, vì các đường thẳng CE và BF nằm trong hai mặt phẳng này nằm trong mặt phẳng BCD và cắt nhau tại điểm P. Một điểm khác là giao điểm Q của đường thẳng AF và CK trong mặt phẳng ACD (Hình 257, b). Rõ ràng, điểm này là tâm khối của mặt ACD. Giao điểm mong muốn là đường PQ.

3) Chúng tôi xây dựng phần được chỉ ra trong điều kiện, sử dụng dấu hiệu của độ song song của các mặt phẳng. Ta vẽ các đường thẳng đi qua các điểm P và Q lần lượt song song với các đường thẳng DB và DA (Hình 257, c). Các đường thẳng này cắt đoạn thẳng CD tại điểm L. Đường thẳng sau dựa trên tính chất của khối tâm của tam giác - nó chia đường trung tuyến của tam giác theo tỷ lệ 2: 1, tính từ đỉnh. Nó vẫn còn để áp dụng định lý Thales. Do đó, hai mặt phẳng PLQ và BDA song song với nhau. Phần mong muốn là tam giác LSN.

Theo cách dựng, các tam giác BCD và SCL đồng dạng với hệ số đồng dạng CE CP = 3 2. Do đó LS = 3 2 BD. Tương tự,

các đáy bằng nhau được đổ: LN = 3 2 AD, NS = 3 2 AB. Điều này ngụ ý rằng các tam giác LSN và ABD đồng dạng với hệ số đồng dạng là 3 2. Theo tính chất của diện tích các tam giác như vậy,

S LNS = 4 9 S ABD. Nó vẫn còn để tìm diện tích của tam giác ABD. Qua-

Vì theo giả thiết, tất cả các cạnh của tứ diện đều bằng a thì S ABD = 4 3 a 2.

Diện tích yêu cầu là 3 1 3 a 2.

Cần lưu ý rằng câu trả lời chỉ phụ thuộc vào diện tích của khuôn mặt ABD. Do đó, bằng nhau của tất cả các cạnh chỉ là một phương tiện để tìm khu vực này. Như vậy, về cơ bản vấn đề này có thể được khái quát hóa.

Câu trả lời. 1) KEF || ABC; 3) 3 1 3 a 2.

 Câu hỏi bảo mật

1. Có đúng là hai mặt phẳng song song nếu mỗi đường thẳng nằm trong một mặt phẳng này lại song song với một mặt phẳng khác không?

2. Các mặt phẳng α và β song song với nhau. Có những đường thẳng cắt nhau nằm trong những mặt phẳng này không?

3. Hai cạnh của một tam giác song song với một mặt phẳng nào đó. Cạnh thứ ba của tam giác có song song với mặt phẳng này không?

4. Hai cạnh của hình bình hành song song với một mặt phẳng nào đó. Có đúng là mặt phẳng của hình bình hành song song với mặt phẳng đã cho không?

5. Đoạn thẳng cắt bởi hai mặt phẳng song song có thể không bằng nhau được không?

6. Thiết diện của hình lập phương có thể là hình thang cân được không? Một hình ngũ giác đều có thể là một thiết diện của hình lập phương không? Có đúng là hai mặt phẳng song song với cùng một đường thẳng thì song song với nhau không?

Các giao tuyến của hai mặt phẳng α và β của mặt phẳng γ thì song song với nhau. Hai mặt phẳng α và β có song song với nhau không?

Ba mặt của một hình lập phương có thể song song với cùng một mặt phẳng được không?

Bài tập đồ họa

1. Hình 258 cho thấy một hình lập phương ABCDA 1 B 1 C 1 D 1, các điểm M, N, K, L, P là trung điểm của các cạnh tương ứng. Điền vào bảng theo mẫu đã cho, chọn cách sắp xếp theo yêu cầu của hai mặt phẳng α và β.

Qua lại

địa điểm

α || β α = β

α × β α || β α = β

2. Trong hình. 259 vẽ tứ diện ABCD, các điểm K, F, M, N, Q là trung điểm của các cạnh tương ứng. Biểu thị:

1) Mặt phẳng đi qua điểm K song song với mặt phẳng ABC;

2) mặt phẳng đi qua đường thẳng BD song song với mặt phẳng MNQ.

3. Xác định thiết diện của hình bởi một mặt phẳng đi qua ba điểm này được thể hiện trong hình vẽ-

kakh 260, a) –e) và 261, a) –d).

4. Dựng hình theo dữ liệu đã cho.

1) Từ các đỉnh của hình bình hành ABCD nằm trong một trong hai mặt phẳng song song kẻ các đường thẳng song song cắt mặt phẳng thứ hai lần lượt tại các điểm A 1, B 1, C 1, D 1.

2) Tam giác A 1 B 1 C 1 là hình chiếu của tam giác ABC lên mặt phẳng song song α. Điểm M là trung trực của BC, M 1 là hình chiếu của điểm M lên mặt phẳng α.

207. Trong hình lập phương ABCDA 1 B 1 C 1 D 1 điểm O, O 1 lần lượt là tâm của các mặt ABCD và A 1 B 1 C 1 C 1 D 1, M là trung điểm của cạnh AB.

1 °) Xác định vị trí tương đối của các mặt phẳng MO 1 O

và ADD 1, ABD 1 và CO 1 C 1.

2 °) Dựng giao điểm của mặt phẳng DCC 1 với đường thẳng MO 1 và giao tuyến của hai mặt phẳng MCC 1 và A 1 D 1 C 1.

3) Tìm thiết diện của hình lập phương song song với mặt phẳng AD 1 C 1 và đi qua điểm O 1 nếu cạnh của hình lập phương bằng a.

208. Trong tứ diện ABCD, các điểm K, L, P lần lượt là tâm của các mặt ABD, BDC, ABC và M là trung điểm của cạnh AD.

1 °) Xác định vị trí tương đối của các mặt phẳng ACD

và KLP; MLK và ABC.

2 °) Vẽ giao điểm của mặt phẳng ABC với đường thẳng ML và giao tuyến của hai mặt phẳng MKL và ABC.

3) Tìm thiết diện của tứ diện bởi mặt phẳng đi qua các điểm K, L và M song song với đường thẳng AD, nếu tất cả các cạnh của tứ diện đều bằng a.

209. Cho hình lập phương ABCDA 1 B 1 C 1 D 1. Các điểm L, M, M 1 lần lượt là trung điểm của các cạnh AB, AD và A 1 D 1.

1 °) Xác định vị trí tương đối của các mặt phẳng B 1 D 1 D

và LMM1.

2) Dựng mặt phẳng đi qua điểm M song song với mặt phẳng ACC 1.

3) Dựng thiết diện của hình lập phương với mặt phẳng đi qua điểm M 1 song song với mặt phẳng CDD 1.

4) Xác định vị trí tương đối của các mặt phẳng MA 1 IN 1

và CDM1.

5) Dựng mặt phẳng đi qua đường thẳng C 1 D 1 song song với mặt phẳng CDM 1.

210. Trong hình chóp tứ giác đều SABCD có tất cả các cạnh bằng nhau. Các điểm L, M, N lần lượt là trung điểm của các cạnh AS, BS, CS.

1 °) Xác định vị trí tương đối của: các đường thẳng LM và BC; đường thẳng LN và mặt phẳng ABD; mặt phẳng LMN và BDC.

2 °) Chứng minh rằng các tam giác ABC và LMN đồng dạng.

3) Dựng thiết diện của hình chóp với mặt phẳng AMN; mặt phẳng LMN; máy bay LBC.

4 *) Thiết diện của hình chóp đi qua đỉnh S có diện tích lớn nhất?

Sự song song của đường thẳng và mặt phẳng

Trong tứ diện SABC, các mặt đều là tam giác đều. Các điểm L, M, N lần lượt là trung điểm của các cạnh AS, BS, CS. 1 °) Xác định vị trí tương đối của đường LM và BC. 2 °) Xác định vị trí tương đối của đường thẳng LN và mặt phẳng ABC.

3) Chứng minh rằng các tam giác LMN và ABC đồng dạng.

Dựng thiết diện của hình lập phương là: 1 °) là tam giác đều; 2) một ngũ giác.

217. Dựng thiết diện là hình bình hành của tứ diện.

218 °. Chứng minh rằng các mặt đối diện của hình bình hành song song với nhau.

219. Chứng minh rằng tập hợp tất cả các đường thẳng đi qua một điểm cho trước và song song với một mặt phẳng cho trước tạo thành một mặt phẳng song song với một mặt phẳng cho trước.

220. Cho bốn điểm A, B, C, D không nằm trong cùng một mặt phẳng. Chứng minh rằng mỗi mặt phẳng song song với các đường thẳng AB và CD cắt các đường thẳng AC, AD, BD, BC tại các đỉnh của hình bình hành.

221. Chứng minh rằng một mặt phẳng và một đường thẳng không thuộc mặt phẳng này song song với nhau nếu chúng cùng song song với một mặt phẳng.

222. Qua giao điểm O của các đường chéo của hình lập phương ABCDA 1 B 1 C 1 D 1 kẻ một mặt phẳng song song với mặt ABCD. Mặt phẳng này cắt các cạnh BB 1 và CC 1 lần lượt tại các điểm M và N. Chứng minh rằng góc MON là đúng.

223. Chứng minh rằng hai mặt phẳng song song với nhau khi và chỉ khi mỗi đường thẳng cắt một trong hai mặt phẳng cũng cắt nhau.

224 *. Trong hình chóp tam giác SABC qua các đoạn thẳng AD và CE, trong đó D là trung điểm của SB và E là trung điểm của SA, vẽ các thiết diện của hình chóp song song với nhau.

225. Tìm địa điểm hình học:

1) trung điểm của tất cả các đoạn thẳng có đầu mút thuộc hai mặt phẳng song song cho trước; 2 *) trung điểm của đoạn thẳng có đầu mút thuộc hai đường thẳng cắt nhau đã cho.

226 *. Cạnh AB của tam giác ABC nằm trong mặt phẳng α song song với mặt phẳng β. Tam giác đều А 1 В 1 С 1 là hình chiếu song song của tam giác ABC lên mặt phẳng β; AB = 5, BC = 6, AC = 9.

1) Thiết lập vị trí tương đối của các đoạn thẳng AB và A 1 B 1,

BC và B1 C1, A1 C1 và AC.

2) Tìm diện tích tam giác A 1 B 1 C 1.

227 *. Hai đường giao nhau được đưa ra. Cho biết tập hợp tất cả các điểm trong không gian mà qua đó bạn có thể vẽ một đường thẳng cắt nhau của hai đường thẳng đã cho.

Định nghĩa cơ bản

Hai mặt phẳng được gọi là

song song,

nếu chúng không có điểm chung.

Các tuyên bố chính

Dấu hiệu song song - Nếu hai giao điểm của hai đường thẳng thuộc một mặt phẳng của mặt phẳng lần lượt song song với hai đường thẳng của mặt phẳng thứ hai thì các mặt phẳng này

các xương song song với nhau.

Định lý về giao tuyến Nếu hai giao tuyến của hai mặt phẳng song song được một mặt phẳng thứ ba cắt bởi một mặt phẳng thì các đường của giao tuyến thứ ba của mặt phẳng

chúng song song với nhau.

a α, b α, a × b, c β, d β, a || c, b || d α || β

α || β, a = γ∩α, b = γ∩β a || b

M α

β: α || β, М β

Chuẩn bị cho chuyên đề

người được đánh giá về chủ đề "Song song của đường thẳng và mặt phẳng"

Nhiệm vụ tự kiểm soát

1. Bốn điểm không cùng thuộc một mặt phẳng. Một số ba trong số chúng có thể nằm trên cùng một đường thẳng không?

2. Ba mặt phẳng khác nhau có thể có hai điểm chung?

3. Hai đường thẳng chéo nhau có thể đồng thời song song với đường thẳng thứ ba không?

4. Có đúng là thẳng không a và b không song song nếu không có đường thẳng c nào song song với a và b?

5. Các đoạn thẳng bằng nhau có thể có các phép chiếu không bằng nhau không?

6. Một tia có thể là hình chiếu song song của một đường thẳng được không?

7. Một hình vuông có thể là một hình lập phương?

8. Có đúng là chỉ có thể vẽ một mặt phẳng đi qua một điểm cho trước trong không gian, song song với một đường thẳng cho trước không?

9. Có phải luôn luôn có thể vẽ một đường thẳng đi qua một điểm cho trước song song với hai mặt phẳng cho trước không chứa điểm này?

10. Có thể vẽ mặt phẳng song song qua hai đường thẳng chéo nhau không?

Câu trả lời cho các nhiệm vụ để tự kiểm soát I

Mẫu thử

Hai hình bình hành ABCD và ABC 1 D 1 nằm trong hai mặt phẳng khác nhau.

1 °) Xác định vị trí tương đối của các đường thẳng CD và C 1 D 1.

2 °) Xác định vị trí tương đối của đường thẳng C 1 D 1 và mặt phẳng

3 °) Dựng đường giao tuyến của hai mặt phẳng DD 1 С 1 và ВСС 1.

4 °) Xác định vị trí tương đối của hai mặt phẳng ADD 1 và BCC 1.

5) Qua điểm M chia đoạn AB theo tỉ lệ 2: 1, kể từ điểm A kẻ mặt phẳng α song song với mặt phẳng C1 BC. 6) Dựng giao điểm của đường thẳng AC với mặt phẳng α và tìm tỉ số điểm chia đoạn thẳng AC.

Sự sắp xếp lẫn nhau của các mặt phẳng thẳng trong không gian

Lượng giác

Bạn đã xử lý các hàm số lượng giác trong các bài học hình học rồi. Cho đến nay, các ứng dụng của chúng chủ yếu chỉ giới hạn trong việc giải các hình tam giác, tức là việc tìm kiếm một số yếu tố của một hình tam giác từ những người khác. Từ lịch sử toán học, người ta đã biết rằng sự xuất hiện của lượng giác gắn liền với phép đo độ dài và góc. Tuy nhiên, hiện nay quả cầu

của cô ứng dụng rộng hơn nhiều so với thời cổ đại.

Từ "lượng giác" bắt nguồn từ tiếng Hy Lạp τριγωνον

(trigonon) - tam giác và µετρεω (metreo) - đo lường, thay đổi

Tôi đang chết đuối. Nó có nghĩa đen là đo hình tam giác.

V Chương này hệ thống hóa tài liệu mà bạn đã biết từ khóa học hình học, tiếp tục nghiên cứu các hàm lượng giác và ứng dụng của chúng để mô tả các quá trình tuần hoàn, cụ thể là chuyển động quay, các quá trình dao động, v.v.

Hầu hết các ứng dụng của lượng giác liên quan cụ thể đến các quá trình tuần hoàn, tức là các quá trình lặp lại đều đặn. Thời gian mặt trời mọc và lặn, sự thay đổi trong các mùa, vòng quay của bánh xe là những ví dụ đơn giản nhất về các quá trình này. Các dao động cơ học và điện từ cũng là những ví dụ quan trọng của các quá trình tuần hoàn. Vì vậy, việc nghiên cứu các quá trình tuần hoàn là một nhiệm vụ quan trọng. Và vai trò của toán học trong giải pháp của nó là quyết định.

chuẩn bị học chủ đề "Hàm số lượng giác"

Nên bắt đầu nghiên cứu chủ đề "Hàm số lượng giác" bằng cách nhắc lại các định nghĩa và tính chất của các hàm số lượng giác về góc của tam giác và ứng dụng của chúng để giải cả hình chữ nhật và hình tam giác tùy ý.

Sin, côsin, tiếp tuyến, phương của các góc hình chữ nhật

Tam giác

Bảng 24

Sin của một góc nhọn là tỷ số của chân đối diện với cạnh huyền:

sin α = a c.

Côsin của một góc nhọn là tỷ số của chân kề cạnh cạnh huyền:

cosα = b c.

Tiếp tuyến của một góc nhọn là tỷ số của chân đối diện với chân kề bên:

tg α = a b.

Cotang của một góc nhọn là tỷ số của chân liền kề với chân đối diện:

ctgα = a b.

Hình sin, côsin, tiếp tuyến, phương ngang của các góc từ 0 ° đến 180 °

Bảng 25

sin α = R y; cosα = R x;

tg α = x y; ctg α = x y.

(X; tại) - tọa độ điểm MỘT nằm trên hình bán nguyệt phía trên, α - góc tạo bởi bán kính OA vòng tròn với trục X.

Giá trị sin, cosine, tiếp tuyến, cotang

một số góc

Bảng 26

Mũi tiêm t

Giải các tam giác tùy ý

Bảng 27

Định lý sin

Các cạnh của một tam giác tỷ lệ với các sin của các góc đối diện:

tội Mộtα = tội bβ = tội Cγ .

Định lý cosine

Bình phương của một cạnh tùy ý của một tam giác bằng tổng bình phương của hai cạnh khác mà không nhân đôi các cạnh này theo cosin của góc giữa chúng:

C2 = Một2 + b2 − 2 ab cos γ , b2 = Một2 + C2 − 2 AC cos β , Một2 = b2 + C2 − 2 bc cos α .

Diện tích của một tam giác là một nửa tích của hai cạnh của nó và sin của góc giữa chúng:

S= 1 2 abtộiγ = 1 2 ACtộiβ = 1 2 bctộiα .

Nhận dạng lượng giác cơ bản

5. So sánh tổng các sin của các góc nhọn của một tam giác vuông tùy ý (chúng tôi ký hiệu nó bằngMỘT) với một.

< 1. B.MỘT= 1.

> 1. G. Không thể so sánh được. Sắp xếp các số theo thứ tự tăng dần: Một= sin 30 °, b= cos 30 °,

= tg 30 °.

< b< C. B.Một< C< b. VC< Một< b. G.b< Một< C.

So sánh các góc nhọn α và β mà không cần tính toán có nghĩa là 7.

15. Chỉ định tọa độ điểmMỘT nằm trên một đường tròn bán kính 1 (xem Hình.).

(−1; 0). B.(1; 0).

(0; − 1). G.(0; 1).MỘT.V

Mọi thao tác công nghệ có thể được thực hiện với độ chính xác nhất định, có nghĩa là kích thước của chi tiết thu được do quá trình gia công sẽ không lý tưởng, chúng có thể dao động trong một phạm vi nhất định. Để đáp ứng các điều kiện thu thập và đảm bảo hoạt động đáng tin cậy của bộ phận trong các điều kiện đã cho, cần thiết lập khoảng cho phép mà kích thước cuối cùng phải giảm. Khoảng này có thể điều chỉnh không chỉ kích thước tuyến tính hoặc đường kính, mà còn cả hình dạng hoặc vị trí tương đối của các bề mặt.

Dung sai hình dạng và vị trí được nhà thiết kế ấn định dựa trên các điều kiện lắp ráp và đặc thù công việc của bộ phận trong cơ cấu.

Các loại dung sai hình thức

Dung sai hình dạngđược gọi là giá trị lớn nhất cho phép của độ lệch của hình dạng.

Dung sai hình thức- đây là một khu vực trên mặt phẳng hoặc trong không gian, trong đó tất cả các điểm của phần tử được xem xét phải nằm trong khu vực chuẩn hóa, chiều rộng hoặc đường kính của chúng được xác định bởi giá trị dung sai và vị trí liên quan đến phần tử thực bằng phần tử liền kề.

Sai lệch và dung sai của hình thức

Có các dung sai sau cho sai lệch hình dạng:

• Độ lệch so với độ thẳng trong mặt phẳng
• lồi lõm
• sự tập trung
• Sai lệch so với mặt phẳng và dung sai độ phẳng
• Lồi
• Lực hấp dẫn
• Độ lệch độ tròn và dung sai độ tròn
• Noãn sào
• Cắt
• Độ lệch hình trụ và dung sai hình trụ
• Sai lệch và dung sai của biên dạng của mặt cắt dọc của bề mặt hình trụ
• Độ lệch của biên dạng của mặt cắt dọc
• Côn
• Thùng
• Giống yên ngựa

Dung sai được biểu thị bằng các ký hiệu đặc biệt.

Các loại dung sai vị trí

Vị trí khoan dung- giới hạn giới hạn giá trị cho phép của độ lệch vị trí.

Sự phân biệt được thực hiện giữa dung sai vị trí và dung sai định hướng.

Trường dung sai vị trí- một khu vực trên một mặt phẳng hoặc trong không gian, trong đó cần đặt một phần tử liền kề hoặc một mặt phẳng đối xứng, một trục, một tâm trong khu vực chuẩn hóa, đường kính hoặc chiều rộng của chúng được xác định bởi giá trị dung sai và giá trị tương đối vị trí được xác định bởi vị trí danh nghĩa của phần tử được đề cập.

Sai lệch và dung sai của vị trí

Có các loại dung sai vị trí sau:

• Độ lệch song song và độ lệch song song
• Dung sai độ lệch và độ vuông góc
• Độ lệch và độ nghiêng
• Sai lệch và dung sai căn chỉnh
• Bán kính dung sai
• Sai lệch và dung sai đối xứng
• Sai lệch vị trí và dung sai vị trí
• Dung sai đường kính
• Bán kính dung sai
• Độ lệch giao lộ và dung sai giao cắt trục
• Dung sai đường kính
• Bán kính dung sai

Tổng dung sai

Có một số loại dung sai tóm tắt cho hình dạng và vị trí.

• Chạy xuyên tâm
• Tổng số lần chạy hướng tâm
• Chạy khuôn mặt
• Chạy toàn bộ khuôn mặt
• Chạy theo một hướng nhất định
• Sai lệch và dung sai của hình dạng của một biên dạng nhất định
• Sai lệch và dung sai của hình dạng của một bề mặt nhất định

Các dung sai này được biểu thị bằng các ký hiệu.

Chỉ định dung sai của hình dạng và vị trí trong bản vẽ

Dung sai hình thức và vị trí được thể hiện trong bản vẽ dưới dạng khung, được chia thành nhiều phần. Trong phần đầu tiên, ký hiệu đồ họa của dung sai được mô tả, trong phần thứ hai - giá trị số của dung sai, trong phần thứ ba và phần tiếp theo - ký hiệu bằng chữ cái của một hoặc nhiều cơ sở.

Trong trường hợp không có cơ sở dung sai, khung chỉ bao gồm hai phần. Các ví dụ về khung dung sai hình dạng và vị trí được thể hiện trong hình.

Hình bên trái cho thấy khung có dung sai hình dạng (độ lệch cho phép so với độ thẳng), bên phải có dung sai vị trí (độ lệch cho phép so với độ song song).

Khung được làm bằng các đường mảnh. Chiều cao của văn bản trong khung phải phù hợp với kích thước phông chữ của các số thứ nguyên. Một đường kết thúc bằng mũi tên được vẽ từ khung dung sai đến bề mặt hoặc đường dẫn.

Các dấu hiệu có thể được chỉ ra trước giá trị số của dung sai:

• ф - nếu trường dung sai hình trụ hoặc hình tròn được biểu thị bằng đường kính
• R - nếu trường hình trụ hoặc hình tròn được biểu thị bằng bán kính
• T - nếu trường dung sai của giao điểm của các trục, đối xứng, được giới hạn bởi hai đường thẳng hoặc mặt phẳng song song theo đường kính.
• Т / 2 - trong cùng trường hợp với Т, chỉ trong biểu thức bán kính
• Hình cầu - cho trường dung sai hình cầu.

Nếu dung sai không được áp dụng cho toàn bộ bề mặt mà chỉ cho một khu vực nhất định, thì dung sai đó được biểu thị bằng một đường chấm gạch ngang.

Một số dung sai có thể được chỉ định cho một phần tử, trong trường hợp này, các khung được vẽ bên trên khung kia.

Thông tin bổ sung có thể được chỉ ra bên trên hoặc bên dưới khung.

Thông tin về dung sai hình thức và vị trí có thể được chỉ định trong.

Dung sai căn chỉnh không xác định phù hợp với GOST 25069-81.

Dung sai phụ thuộc

Dung sai vị trí phụ thuộc được biểu thị bằng ký hiệu sau.

Ký hiệu này có thể được đặt sau giá trị số của dung sai nếu dung sai phụ thuộc có liên quan đến kích thước thực của phần tử được đề cập. Ngoài ra, ký hiệu có thể được đặt sau ký hiệu chữ cái (nếu nó không có, thì trong trường thứ ba của khung) nếu dung sai phụ thuộc được kết hợp với kích thước thực của phần tử cơ sở.

Gán dung sai hình dạng và vị trí

Bộ phận càng được chế tạo chính xác, thì càng cần có các công cụ chính xác hơn để sản xuất và kiểm soát kích thước. Điều này sẽ tự động làm tăng chi phí của nó. Nó chỉ ra rằng chi phí sản xuất một bộ phận phần lớn phụ thuộc vào độ chính xác cần thiết trong sản xuất của nó. Điều này có nghĩa là người thiết kế phải chỉ định những dung sai thực sự cần thiết để lắp ráp và hoạt động đáng tin cậy của cơ cấu. Khoảng thời gian cho phép cũng nên được ấn định dựa trên các điều kiện thu thập và thực hiện.

Các giá trị số của dung sai hình thức

Tùy thuộc vào cấp độ chính xác, các giá trị tiêu chuẩn cho dung sai hình thức được thiết lập.

Dung sai độ phẳng và độ thẳng

Kích thước danh nghĩa trong trường hợp này là chiều dài danh nghĩa của mặt cắt được tiêu chuẩn hóa.

Dung sai của độ tròn, hình trụ, biên dạng mặt cắt dọc

Các dung sai này được ấn định trong trường hợp chúng phải nhỏ hơn dung sai kích thước.

Kích thước danh nghĩa là đường kính bề mặt danh nghĩa.

Dung sai của độ vuông, độ song song, độ nghiêng, độ chảy mặt

Kích thước danh nghĩa khi ấn định dung sai cho độ song song, độ vuông góc, độ dốc được hiểu là diện tích chuẩn hóa danh nghĩa hoặc chiều dài danh nghĩa của toàn bộ bề mặt được khống chế.

Dung sai của đường chạy xuyên tâm, tính đối xứng, độ đồng trục của giao điểm của các trục theo đường kính

Khi ấn định dung sai dòng chảy xuyên tâm, kích thước danh nghĩa là đường kính danh nghĩa của bề mặt được đề cập.

Trong trường hợp ấn định dung sai đối xứng, giao điểm của trục liên kết, kích thước danh nghĩa là đường kính danh nghĩa của bề mặt hoặc kích thước danh nghĩa giữa các bề mặt tạo thành phần tử được đề cập.

Tất cả những ai đã từng học hoặc đang học ở trường đều phải đối mặt với những khó khăn khác nhau khi theo học những môn học nằm trong chương trình giảng dạy của Bộ Giáo dục.

Bạn gặp khó khăn gì

Học ngôn ngữ đi kèm với việc ghi nhớ các quy tắc ngữ pháp có sẵn và các ngoại lệ chính đối với chúng. Môn thể dục đòi hỏi ở học sinh rất nhiều tính toán, thể chất tốt và tính kiên nhẫn cao.

Tuy nhiên, những khó khăn nảy sinh trong việc nghiên cứu các ngành chính xác không thể so sánh được với bất cứ điều gì. Một đại số có chứa những cách phức tạp để giải quyết các vấn đề cơ bản. Vật lý với một bộ công thức phong phú cho các định luật vật lý. Hình học và các phần của nó, dựa trên các định lý và tiên đề phức tạp.

Một ví dụ là các tiên đề giải thích lý thuyết về tính song song của các mặt phẳng, điều này phải được ghi nhớ, vì chúng là nền tảng của toàn bộ chương trình học ở trường về phép đo lập thể. Chúng ta hãy cố gắng tìm ra cách nó có thể được thực hiện dễ dàng hơn và nhanh hơn.

Các mặt phẳng song song bằng các ví dụ

Tiên đề chỉ ra sự song song của các mặt phẳng nghe như sau: " Hai mặt phẳng bất kỳ chỉ được coi là song song nếu chúng không chứa điểm chung”, Tức là không giao nhau với nhau. Để hình dung bức tranh này chi tiết hơn, như một ví dụ cơ bản, bạn có thể trích dẫn tỷ lệ giữa trần và sàn hoặc các bức tường đối diện trong một tòa nhà. Nó trở nên rõ ràng ngay lập tức ý nghĩa của nó, và cũng xác nhận thực tế rằng những mặt phẳng này trong trường hợp thông thường sẽ không bao giờ cắt nhau.

Một ví dụ khác là cửa sổ lắp kính hai lớp, nơi các tấm kính đóng vai trò như mặt phẳng. Chúng cũng sẽ không tạo thành giao điểm với nhau trong bất kỳ trường hợp nào. Ngoài ra, bạn có thể thêm giá sách, khối Rubik, nơi các mặt phẳng là mặt đối diện của nó và các yếu tố khác của cuộc sống hàng ngày.

Các mặt phẳng đang xét được ký hiệu bằng một dấu hiệu đặc biệt dưới dạng hai đường thẳng "||", minh họa rõ ràng tính song song của các mặt phẳng. Do đó, bằng cách sử dụng các ví dụ thực tế, bạn có thể hình thành nhận thức rõ ràng hơn về chủ đề, và do đó, bạn có thể chuyển sang xem xét các khái niệm phức tạp hơn.

Lý thuyết về mặt phẳng song song được áp dụng ở đâu và như thế nào

Khi học một môn hình học, học sinh phải giải quyết các bài toán linh hoạt, trong đó thường phải xác định tính song song của đường thẳng, đường thẳng và mặt phẳng với nhau hoặc sự phụ thuộc của các mặt phẳng với nhau. Phân tích điều kiện hiện có, mỗi nhiệm vụ có thể được quy cho bốn lớp chính của hình học rắn.

Lớp thứ nhất bao gồm các nhiệm vụ với điều kiện cần xác định độ song song của một đường thẳng và một mặt phẳng giữa chúng. Giải pháp của nó được rút gọn thành chứng minh của định lý cùng tên. Muốn vậy, bạn cần xác định xem đối với đường thẳng không thuộc mặt phẳng đang xét có đường thẳng song song nằm trong mặt phẳng này hay không.

Loại bài toán thứ hai bao gồm những bài toán trong đó sử dụng dấu của phép song song phẳng. Nó được sử dụng để đơn giản hóa quá trình chứng minh, do đó giảm đáng kể thời gian tìm ra giải pháp.

Lớp tiếp theo bao gồm một loạt các vấn đề về sự tương ứng của các đường thẳng với các tính chất cơ bản của phép song song phẳng. Giải pháp cho các bài toán của lớp thứ tư bao gồm việc xác định xem điều kiện của sự song song của các mặt phẳng có được thỏa mãn hay không. Biết chính xác cách thức chứng minh của một vấn đề cụ thể xảy ra, học sinh sẽ dễ dàng điều hướng hơn khi sử dụng kho tiên đề hình học hiện có.

Do đó, các bài toán, điều kiện yêu cầu xác định và chứng minh tính song song của đường thẳng, một đường thẳng và một mặt phẳng hoặc hai mặt phẳng với nhau, được rút gọn thành việc lựa chọn đúng một định lý và một lời giải theo tập hợp đã có quy tắc.

Về sự song song của một đường thẳng và một mặt phẳng

Tính song song của một đường thẳng và một mặt phẳng là một chủ đề đặc biệt trong hình học lập thể, vì nó là khái niệm cơ bản dựa trên tất cả các tính chất tiếp theo của tính song song của các hình hình học.

Theo tiên đề đã có, trong trường hợp hai điểm thuộc một đường thẳng cùng thuộc một mặt phẳng nào đó thì ta có thể kết luận rằng đường thẳng này cũng nằm trong đó. Trong tình huống này, rõ ràng là có thể có ba lựa chọn về vị trí của đường thẳng so với mặt phẳng trong không gian:

1. Đường thẳng thuộc mặt phẳng.
2. Có một giao điểm chung của một đường thẳng và một mặt phẳng.
3. Không có giao điểm của đường thẳng và mặt phẳng.

Đặc biệt, chúng tôi quan tâm đến phương án cuối cùng, khi không có giao điểm nào. Khi đó chúng ta mới có thể nói rằng một đường thẳng và một mặt phẳng là song song với nhau. Do đó, điều kiện của định lý chính về tiêu chí của sự song song của một đường thẳng và một mặt phẳng đã được khẳng định, điều này nói lên rằng: "Nếu đường thẳng không thuộc mặt phẳng đang xét song song với đường thẳng nào trên mặt phẳng này thì đường thẳng đang xét cũng song song với mặt phẳng này."

Sự cần thiết phải sử dụng tính năng song song

Tính song song của mặt phẳng thường được sử dụng để tìm ra các giải pháp đơn giản cho các bài toán về mặt phẳng. Bản chất của tính năng này như sau: “ Nếu có hai đường thẳng chéo nhau cùng nằm trong một mặt phẳng, song song với hai đường thẳng thuộc một mặt phẳng khác thì các mặt phẳng đó có thể gọi là song song».

Định lý bổ sung

Ngoài việc sử dụng tiêu chí chứng minh tính song song của các mặt phẳng, trong thực tế, người ta có thể bắt gặp ứng dụng của hai định lý bổ sung khác. Đầu tiên được trình bày dưới dạng sau: " Nếu một trong hai mặt phẳng song song song song với mặt phẳng thứ ba thì mặt phẳng thứ hai cũng song song với mặt phẳng thứ ba hoặc hoàn toàn trùng với nó».

Dựa trên việc sử dụng các định lý rút gọn, luôn có thể chứng minh được tính song song của các mặt phẳng trong không gian đang xét. Định lý thứ hai phản ánh sự phụ thuộc của mặt phẳng vào đường trung trực và có dạng: “ Nếu hai mặt phẳng không ghép vuông góc với một đường thẳng nào đó thì chúng được coi là song song với nhau».

Khái niệm về điều kiện cần và đủ

Với cách giải lặp đi lặp lại của các bài toán chứng minh tính song song của các mặt phẳng, một điều kiện cần và đủ để các mặt phẳng song song đã được suy ra. Biết rằng bất kỳ mặt phẳng nào cho bởi một phương trình tham số có dạng: A 1 x + B 1 y + C 1 z + D 1 = 0. Điều kiện của chúng tôi dựa trên việc sử dụng một hệ phương trình xác định sự sắp xếp của các mặt phẳng trong không gian và được biểu diễn bằng công thức sau: " Để chứng minh sự song song của hai mặt phẳng, điều cần và đủ là hệ phương trình mô tả các mặt phẳng này không đồng nhất, nghĩa là không có nghiệm.».

Các tính chất cơ bản

Tuy nhiên, khi giải các bài toán hình học, việc sử dụng tính chất song song không phải lúc nào cũng đầy đủ. Đôi khi nảy sinh tình huống cần chứng minh tính song song của hai hay nhiều đường thẳng trong các mặt phẳng khác nhau hoặc sự bằng nhau của các đoạn thẳng nằm trên các đường thẳng này. Đối với điều này, các thuộc tính của song song mặt phẳng được sử dụng. Trong hình học, chỉ có hai trong số chúng.

Tính chất đầu tiên giúp ta có thể đánh giá tính song song của các đường thẳng trong một số mặt phẳng nhất định và được trình bày dưới dạng sau: “ Nếu hai mặt phẳng song song cắt một phần ba thì các đường thẳng tạo bởi các giao tuyến cũng sẽ song song với nhau.».

Ý nghĩa của tính chất thứ hai là chứng minh sự bằng nhau của các đoạn nằm trên các đường thẳng song song. Diễn giải của nó được trình bày dưới đây. " Nếu chúng ta xem xét hai mặt phẳng song song và bao quanh một khu vực giữa chúng, thì có thể lập luận rằng độ dài của các đoạn được hình thành bởi khu vực này sẽ bằng nhau».