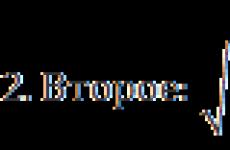Kuljettavat kulmat trigonometriseen ympyrään. Positiiviset ja negatiiviset kulmat. Kulmien jakelu neljäsosaan. Kulmamittaus voi haluttomia olla negatiivinen
Kulma: ° π Rad \u003d
Muunna: Radiansasteisto 0 - 360 ° 0 - 2π Positiivinen negatiivinen laskenta
Kun suora leikkaa, saadaan neljä eri aluetta suhteessa risteyspisteeseen.
Näitä uusia alueita kutsutaan kulmat.
Kuvassa on 4 eri kulmaa, jotka on muodostettu Direct AB: n ja CD: n risteyksestä
Tyypillisesti kulmat mitataan asteina, mikä on osoitettu °. Kun esine suorittaa koko ympyrän, eli siirtyminen pisteestä D kautta B, C, A ja sitten takaisin D: hen, he sanovat, että se kääntyi 360 astetta (360 °). Siten tutkinto on $ frac (1) (360) $ ympyrä.
Kulmat yli 360 astetta
Puhuimme, kun esine tekee koko ympyrän pisteen ympärillä, sitten se kulkee 360 \u200b\u200b°, kun esine tekee useammasta ympyrästä, se tekee yli 360 asteen kulman. Tämä on yleinen ilmiö arjessa. Pyörä kulkee monia piirejä, kun auto liikkuu, se muodostaa suuremman kulman, joka on suurempi kuin 360 °.
Jotta voit selvittää syklien määrän (piirejä), kun objekti pyörii, harkitsemme useita kertoja, jotka sinun on lisättävä 360 itsellesi, jotta saat numeron yhtä suureksi tai pienemmäksi kuin tämä kulma. Samoin löydämme numeron, jonka moninkertaistuimme 360, jotta saat useita pienempiä, mutta lähimpänä tätä kulmaa.
Esimerkki 2.
1. Etsi kulmassa kuvattujen ympyrän määrä
a) 380 °
b) 770 °
c) 1000 °
Päätös
a) 380 \u003d (1 × 360) + 20
Objekti kuvasi yhtä ympyrää ja 20 °
Koska $ 20 ^ (sirc) \u003d \\ frac (20) (360) \u003d \\ frac (1) (18) $ ympyrä
Objekti kuvasi $ 1 \\ frac (1) (18) $ piirejä.
B) 2 × 360 \u003d 720
770 \u003d (2 × 360) + 50
Objekti kuvasi kaksi ympyrää ja 50 °
$ 50 ^ (sirc) \u003d \\ frac (50) (360) \u003d \\ frac (5) (36) $ ympyrä
Objekti kuvattu $ 2 \\ frac (5) (36) $ ympyrä
c) 2 × 360 \u003d 720
1000 \u003d (2 × 360) + 280
$ 280 ^ (sirc) \u003d \\ frac (260) (360) \u003d \\ frac (7) (9) $ piirejä
Objekti kuvasi $ 2 \\ frac (7) (9) $ piirejä
Kun kohde pyörii myötäpäivään, se muodostaa negatiivisen pyörimisen kulman ja kun se pyörii vastapäivään - positiivinen kulma. Tähän asti pidimme vain positiivisia kulmia.
Kaavion muodossa negatiivinen kulma voidaan kuvata alla olevan kuvan mukaisesti. 
Alla oleva luku esittää kulman merkki, joka mitataan kokonaislinjasta, 0-akselista (abskissal akselin akseli) 
Tämä tarkoittaa, että negatiivisen kulman läsnä ollessa voimme saada vastaavan positiivisen kulman.
Esimerkiksi pystysuoran suoran alaosa on 270 °. Kun mitataan negatiivisessa suunnassa, saamme -90 °. Me yksinkertaisesti vähennät 270: n 360: sta. Negatiivinen kulma, lisätään 360, jotta saat vastaavan positiivisen kulman.
Kun kulma on -360 °, tämä tarkoittaa, että kohde teki useamman kuin yhden ympyrän myötäpäivään.
Esimerkki 3.
1. Etsi sopiva positiivinen kulma
a) -35 °
b) -60 °
C) -180 °
d) - 670 °
2. Etsi vastaava negatiivinen kulma 80 °, 167 °, 330 ° ja 1300 °.
Päätös
1. Jos haluat löytää sopivan positiivisen kulman, lisäämme 360 \u200b\u200bkulman arvoon.
a) -35 ° \u003d 360 + (-35) \u003d 360 - 35 \u003d 325 °
b) -60 ° \u003d 360 + (-60) \u003d 360 - 60 \u003d 300 °
c) -180 ° \u003d 360 + (-180) \u003d 360 - 180 \u003d 180 °
d) -670 ° \u003d 360 + (-670) \u003d -310
Tämä tarkoittaa yhtä ympyrää myötäpäivään (360)
360 + (-310) \u003d 50 °
Kulma on 360 + 50 \u003d 410 °
2. Sopivan negatiivisen kulman saamiseksi vähennyksemme 360 \u200b\u200bkulma-arvosta.
80 ° \u003d 80 - 360 \u003d - 280 °
167 ° \u003d 167 - 360 \u003d -193 °
330 ° \u003d 330 - 360 \u003d -30 °
1300 ° \u003d 1300 - 360 \u003d 940 (yksi ympyrä kulki)
940 - 360 \u003d 580 (toinen kierros läpäisi)
580 - 360 \u003d 220 (kolmas ympyrä läpäisi)
220 - 360 \u003d -140 °
Kulma on -360 - 360 - 360 - 140 \u003d -1220 °
Siten 1300 ° \u003d -1220 °
Radian
Radiini on ympyrän keskuksen kulma, johon kaari on päättynyt, jonka pituus on yhtä suuri kuin tämän ympyrän säde. Tämä on kulma-arvon mittayksikkö. Tällainen kulma on noin 57,3 °.
Useimmissa tapauksissa se on ilmoitettu iloinen.
Siten $ 1 Rad \\ noin 57.3 ^ (sirc) $ 
RADIUS \u003d R \u003d OA \u003d OB \u003d AB
BOA-kulma on yhtä suuri kuin yksi radia
Koska ympärysmittainen pituus on $ 2 \\ pi r $, sitten ympyrän $ 2 \\ pi $ radii, mikä tarkoittaa yleensä ympyrän $ 2 \\ pi $ radian.
Radialaiset ilmaistaan \u200b\u200byleensä $ \\ Pi $, jotta vältetään desimaaliset osat laskelmissa. Useimmissa kirjoissa lyhenne rad (Rad) Ei löytynyt, mutta lukijan pitäisi tietää, että kun se tulee kulmaan, se on asetettu $ piin $, ja mittayksiköt tulevat automaattisesti radialaisiksi.
$ 360 ^ (sirc) \u003d 2 \\ pi \\ rad $
180 dollaria ^ (sirc) \u003d \\ pi \\ rad $
$ 90 ^ (sirc) \u003d \\ frac (\\ pi) (2) Rad $
$ 30 ^ (sirc) \u003d \\ frac (30) (180) \\ pi \u003d \\ frac (\\ PI) (6) Rad $
$ 45 ^ (sirc) \u003d \\ frac (45) (180) \\ pi \u003d \\ frac (\\ PI) (4) Rad $
$ 60 ^ (sirc) \u003d \\ frac (60) (180) \\ pi \u003d \\ frac (\\ PI) (3) Rad $
$ 270 ^ (sirc) \u003d \\ frac (270) (180) \\ pi \u003d \\ frac (27) (18) \\ PI \u003d 1 \\ frac (1) (2) \\ PI \\ PI \\ PI \\ PI \\ PI \\ PI \\ PI \\
Esimerkki 4.
1. Muunna 240 °, 45 °, 270 °, 750 ° ja 390 ° radiaanisille $ piin $.
Päätös
Minä moninkertaistan kulmat $ + frac (\\ pi) (180) $.
$ 240 ^ (sirc) \u003d 240 eri frac (\\ pi) (180) \u003d \\ frac (4) (3) \\ pi \u003d 1 frac (1) (3) \\ PI $
120 dollaria ^ (sirc) \u003d 120 eri frac (\\ PI) (180) \u003d \\ frac (2 \\ PI) (3) $
270 dollaria ^ (sirc) \u003d 270 \\ times \\ frac (1) (180) \\ pi \u003d \\ frac (3) (2) \\ pi \u003d 1 \\ frac (1) (2) \\ PI $
750 dollaria ^ (sirc) \u003d 750 eri frac (1) (180) \\ pi \u003d \\ frac (25) (6) \\ pi \u003d 4 \\ frac (1) (6) \\ PI $
$ 390 ^ (sirc) \u003d 390; 1) (180) \\ PI \u003d \\ FRAC (13) (6) \\ PI \u003d 2 \\ FRAC (1) (6) \\ PI $
2. Muunna seuraavat kulmat asteiksi.
a) $ frac (5) (4) \\ PI $
b) $ 3.12 \\ pi $
c) 2.4 RADIANS
Päätös
$ 180 ^ (sirc) \u003d \\ pi $
a) $ + frac (5) (4) \\ PI \u003d \\ frac (5) (4) \\ Times 180 \u003d 225 ^ (sirc) $
b) $ 3.12 \\ pi \u003d 3.12; 180 \u003d 561.6 ^ (sirc) $
c) 1 kiitos \u003d 57,3 °
$ 2.4 \u003d frac (2.4 kertaa 57,3) (1) \u003d 137,52 $
Negatiiviset kulmat ja kulmat yli $ 2 \\ pi $ radian
Negatiivisen kulman muuntamiseksi positiiviseksi, taitamme sen $ 2 \\ pi $.
Jotta voitaisiin muuntaa positiivinen kulma negatiiviseksi, vähennämme $ 2 \\ PI $ siitä.
Esimerkki 5.
1. Muunna $ - frac (3) (4) \\ PI $ ja $ - \\ frac (5) (7) positiivisiksi näkökulmiin radiaaneissa.
Päätös
Lisää nurkkaan $ 2 \\ pi $
$ - \\ flac (3) (4) \\ PI \u003d - \\ PHAC (3) (4) \\ PI + 2 \\ PI \u003d \\ FRAC (5) (4) \\ PI \u003d 1 \\ frac (1) (4) \\ PI $
$ - \\ frac (5) (7) \\ PI \u003d - \\ PHAC (5) (7) \\ PI + 2 \\ PI \u003d \\ FRAC (9) (7) \\ PI \u003d 1 \\ frac (2) (7) \\ PI $
Kun kohde pyörii suurempi kuin $ 2 \\ pi $;, se tekee useammasta kuin yhdestä ympyrästä.
Jotta voidaan määrittää kierrosluvut (ympyrät tai syklit) tällaisessa kulmassa, löydämme tällaisen numeron, joka kertoo, mikä $ 2 \\ PI $ on yhtä suuri tai vähemmän, mutta mahdollisimman lähellä tätä numeroa.
Esimerkki 6.
1. Etsi objektin piirilevien piireiden määrä näissä kulmissa
a) $ -10 \\ pi $
b) $ 9 \\ pi $
c) $ + frac (7) (2) \\ PI $
Päätös
a) $ -10 \\ pi \u003d 5 (-2 \\ PI) $;
$ -2 \\ PI $ tarkoittaa yhtä syklin kohti myötäpäivään, niin tämä tarkoittaa sitä
Kohde teki 5 sykliä myötäpäivään.
b) $ 9 \\ pi \u003d 4 (2 \\ PI) + \\ PI $, $ PI \u003d $ Floor Cycle
Kohde teki neljä ja puoli kierrosta vastapäivään
c) $ + frac (7) (2) \\ pi \u003d 3.5 \\ pi \u003d 2 \\ pi + 1,5 \\ pi $, $ 1,5 \\ pi $ on kolme neljäsosaa $ Cycle (\\ Frac (1.5 \\ PI) (2 \\ PI) \u003d \\ frac (3) (4)) $
Objekti läpäisi yhden ja kolme neljäsosaa syklin vastapäivään
Trigonometria, kuten tiede, syntyi muinaisesta idästä. Ensimmäiset trigonometriset suhteet johtuivat tähtitieteilijöille tarkan kalenterin luomiseksi ja tarkentavat tähdet. Nämä laskelmat kuuluivat pallomaiseen trigonometriaan, kun taas koulukurssissa tutkitaan osapuolten suhteita ja tasaisen kolmion kulmaa.
Trigonometria on osa matematiikan, joka harjoittaa trigonometristen toimintojen ominaisuuksia ja riippuvuutta osapuolten ja kolmiojen kulmien välillä.
Ensimmäisen vuosituhannen kulttuurin ja tieteen kukoistelussa tieton aikakausi on levinnyt muinaisesta idästä Kreikkaan. Mutta Trigonometrian tärkeimmät löydöt ovat arabikalifaatin aviomiehiä. Erityisesti, Turkmenistanin tutkija al-Marazvi tuli toimintoja, kuten Tangentti ja Kotangent, koottu tauluissa sinus arvoja, tangentit ja catangents. Intian tutkijat esittelevät sini- ja kosinin käsite. Trigonometria on omistettu paljon huomiota tällaisten suurten antiikin johtajien, kuten euclidea, archimedes ja Eratotostheeni kirjoituksissa.
Trigonometrian tärkeimmät arvot
Numeerisen argumentin tärkeimmät trigonometriset toiminnot ovat sinus, kosini, tangentti ja opingentti. Jokaisella niistä on oma aikataulu: Sinusoid, kosinida, tansensoidi ja catangensoidi.
Määritettyjen määrien arvojen laskentaperusteet ovat Pythagoreo-lause. Koululaiset ovat tunnetuimpia sanamuodossa: "Pythagoras-housut, kaikki suunnat ovat yhtä suuret," koska todiste on esimerkissä yhtä suuresta suorakulmaisesta kolmion.
Sinus, kosini ja muut riippuvuudet luovat yhteyden terävien kulmien ja minkä tahansa suorakulmaisen kolmioon. Annamme kaavoja näiden arvojen laskemiseksi kulmassa A ja jäljittää trigonometristen toimintojen suhdetta:

Kuten voidaan nähdä, TG ja CTG ovat käänteisiä toimintoja. Jos lähetät Catat A syntiä A ja hypotenuesia ja rullaa B COS A * C: n muodossa, saamme seuraavat kaavat tangenttiin ja kotagentiin:

Trigonometrinen ympyrä
Graafisesti mainittujen arvojen suhde voidaan esittää seuraavasti:

Ympyrä tässä tapauksessa on kaikki mahdollinen kulma a - 0 - 360 °. Kuten kuviosta voidaan nähdä, kukin toiminta ottaa negatiivisen tai positiivisen arvon kulman arvosta riippuen. Esimerkiksi Sin α on "+" -merkin kanssa, jos α kuuluu ympyrän neljännekseen I ja II, eli se on 0 - 180 °. Α: llä 180 ° - 360 ° (III ja IV neljäsosat), SIN α voi olla vain negatiivinen arvo.
Yritetään rakentaa trigonometriset taulukot tiettyihin kulmiin ja selvittää arvojen arvo.

Arvot α ovat 30 °, 45 °, 60 °, 90 °, 180 °, ja niin edelleen - kutsutaan erityisiksi. Trigonometristen toimintojen arvot lasketaan niille ja ne esitetään erikoispöydissä.

Näitä kulmia ei valinnut mitään onnettomuutta. Nimitys π pöydissä on radiaaneja. Rad on kulma, jossa ympärysmittarin pituus vastaa sen sädettä. Tämä arvo otettiin käyttöön yleismaailmallisen riippuvuuden luomiseksi radialaisten laskennan aikana, todellinen sädepituus CM: ssä ei ole väliä.

Trigonometristen toimintojen taulukoissa olevat kulmat vastaavat Radian-arvoja:

Joten, ei ole vaikea arvata, että 2π on täydellinen ympyrä tai 360 °.
Trigonometristen toimintojen ominaisuudet: sinus ja kosini
Jotta voitaisiin harkita ja verrata sinus- ja kosini-, tangenttien ja opintojen pääominaisuuksia, on tarpeen tehdä tehtävät. Tämä voidaan tehdä kaksikerroksisen koordinaattijärjestelmässä sijaitsevan käyrän muodossa.
Harkitse vertailevaa taulukkoa sinusoidien ja kosinidien ominaisuuksista:

| Sinusoidi | Kosinusoid |
|---|---|
| y \u003d sin x | y \u003d cos x |
| ODZ [-1; yksi] | ODZ [-1; yksi] |
| sIN X \u003d 0, x \u003d πk, jossa k ε z | cos x \u003d 0, x \u003d π / 2 + πk, jossa k ε z |
| sIN X \u003d 1, X \u003d π / 2 + 2πk, jossa k ε z | cos x \u003d 1, x \u003d 2πk, jossa k ε z |
| sin x \u003d - 1, x \u003d 3π / 2 + 2πk, jossa k ε z | cos x \u003d - 1, x \u003d π + 2πk, jossa k ε z |
| sIN (-X) \u003d - SIN X, ts. Toiminto on pariton | cos (-x) \u003d cos x, ts. Toiminto on edes |
| toiminnan määräaika, pienin aika - 2π | |
| sIN X\u003e 0, X-omistuksessa I ja II neljäsosaa tai 0 ° - 180 ° (2πk, π + 2πk) | cOS X\u003e 0, X-X-omistuksessa I- ja IV-neljäsosaa tai 270 ° - 90 ° (- π / 2 + 2πk, π / 2 + 2πk) |
| sIN X \u003c0, X-X-omistuksessa III ja IV-neljäsosaa tai 180 ° - 360 ° (π + 2πk, 2π + 2πk) | cOS X \u003c0, X-X: llä ja kolmannella neljänneksellä tai 90 ° - 270 ° (π / 2 + 2πk, 3π / 2 + 2πk) |
| välien nousu [- π / 2 + 2πk, π / 2 + 2πk] | väliaikana [-π + 2πk, 2πk] |
| välillä [π / 2 + 2πk, 3π / 2 + 2πk] | välillä |
| johdannainen (sin x) '\u003d cos x | johdannainen (COS X) '\u003d - SIN X |
Määritä, onko funktio vai ei kovin yksinkertainen. Riittää trigonometrisen ympyrän esittämiseen trigonometristen arvojen merkkejä ja henkisesti "taitettu" aikataulu suhteessa Ox-akseliin. Jos merkit ovat samat, toiminto on edes, muuten - pariton.

Radiaanien käyttöönotto ja sinimuotojen ja kosinidien pääominaisuuksien siirtäminen antaa sinulle mahdollisuuden tuoda seuraava säännöllisyys:

Varmista, että kaava on hyvin yksinkertainen. Esimerkiksi X \u003d π / 2 sinus on 1, samoin kuin kosini x \u003d 0. Voit tarkistaa taulukot tai jäljittää toimintojen toiminnot määritetyille arvoille.
Tangensoidien ja kotansensoidien ominaisuudet
Tangentin ja kotagenttien toimintojen kaaviot eroavat merkittävästi sininoidista ja kosinidistä. TG: n ja CTG: n arvot ovat palanneet toisiinsa.


- Y \u003d TG X.
- Tangententsoidi pyrkii arvoon y x \u003d π / 2 + πk, mutta ei koskaan saavuta niitä.
- Tangentoidin alin positiivinen aika on yhtä suuri kuin π.
- Tg (- X) \u003d - TG X, toisin sanoen toiminto on pariton.
- Tg x \u003d 0, x \u003d πk.
- Toiminto kasvaa.
- TG X\u003e 0, X ε (πk, π / 2 + πk).
- TG X \u003c0, X ε (- π / 2 + πk, πk).
- Johdannainen (TG X) '\u003d 1 / COS 2 \u2061X.
Harkitse tekstin alapuolella olevien kandongensoidien graafista kuvaa.

Kotagensoidsin pääominaisuudet:
- Y \u003d CTG X.
- Toisin kuin sinus ja kosini, Tangentenoid Y: ssä se voi ottaa monien voimassa olevien numeroiden arvot.
- Kothangensoid pyrkii arvoihin y x \u003d πk, mutta ei koskaan saavuta heitä.
- Katangensoidin pienin positiivinen jakso on yhtä suuri kuin π.
- CTG (- X) \u003d - CTG X, eli toiminto on pariton.
- CTG X \u003d 0, X \u003d π / 2 + πk.
- Toiminto laskee.
- CTG X\u003e 0, X ε (πk, π / 2 + π).
- CTG x \u003c0, x ε (π / 2 + πk, πk).
- Johdannainen (CTG X) '\u003d - 1 / SIN 2 \u2061X FIX
OA: n ja OB: n eri palkkien pari, joka on peräisin yhdestä pisteestä O, kutsutaan kulmaksi ja on merkitty symbolilla (A, B). Piste O on nimeltään kulman huippu ja UB UB: n säteet - kulman sivut. Jos A ja B - kaksi pistettä OA ja OB-säteet, sitten (A, B) on myös merkitty AOS: n symboli (kuva 1.1).
Kulmaa (A, B) kutsutaan laajentuneeksi, jos OA: n ja OB: n säteet nousevat yhdestä pisteestä yhdestä suorasta ja eivät ole samansuuntaisia \u200b\u200b(tämä on vastakkain suunnattu).

Kuva.1.1
Kaksi kulmaa pidetään yhtä suurina, jos yksi kulma voidaan levittää toiseen siten, että kulmien sivu on samat. Bisector-kulmaa kutsutaan säteenä, joka on alussa kulman yläosassa, jakamalla kulma kahteen samankaltaiseen kulmaan.
Sanotaan, että OS: n säde, joka on peräisin kulman AO: n yläosasta, sijaitsee sen osapuolten välillä, jos se ylittää AV: n segmentin (kuva 1.2). Sanotaan, että piste c sijaitsee kulman sivujen välissä, jos säde voidaan pitää tämän kohdan läpi kulman yläosassa, joka sijaitsee kulman sivujen välillä. Kulman sivujen välinen kaikki koneen kohta on kulman sisäpuolella (kuvio 1.3). Tason pisteitä, jotka eivät kuulu sisäiseen alueeseen ja kulman sivut muodostavat kulman ulomman alueen.
Kulma (A, B) pidetään enemmän kulmaa (C, D), jos kulma (C, D) voidaan asettaa kulmaan (A, B) niin, että yhden parin yhdistelmän jälkeen toinen puoli Kulma (C, D) on kulman (A, B) sivujen välillä. Kuviossa 1 1.4 AOS enemmän AOS.
Anna säteen liesiä kulman (A, B) sivujen välillä (kuva 1.5). Rateat A, C ja C, B muodostavat kaksi kulmaa. Kulmasta (A, B) He sanovat, että se on kahden kulman (A, C) ja (C, B) summa ja kirjoittaa: (a, b) \u003d (a, c) + (c, b) .

Kuva.3
Yleensä geometryssä he käsittelevät pienempiä kulmia kuin sovittiin. Kuitenkin kahden kulman lisäämisen seurauksena kulma voidaan näyttää olevan käytössä. Tässä tapauksessa koneen osa, jota pidetään kulman sisäisellä alueeksi, on merkitty kaarella. Kuviossa 1 1.6 Kulman AOS: n sisäpuoli, joka on saatu AOC: n ja OV: n kulmien lisäämisen seurauksena, merkitään kaarella.

Kuva.5.
On myös suuria 360 ° kulmia. Tällaiset kulmat muodostetaan esimerkiksi tason potkurin pyörimisellä, rummun pyöriminen, johon köysi on haava ja niin edelleen.
Tulevaisuudessa kunkin kulman harkitsemisen yhteydessä suostut pitämään tämän kulman puolelta alkuperäisestä puolueestaan \u200b\u200bja toinen on lopullinen osapuoli.
Esimerkiksi kulma, esimerkiksi AO: n kulma (kuva 1.7), voidaan saada liikuteltavan säteen pyörimisen seurauksena kulman (OA) alkupuolen yläpuolelle. Mittaamme tämän kulman, kun otetaan huomioon OT: n ympärillä tehtyjen kierrosten täydellinen määrä sekä suunta, jossa pyöritys tapahtui.
Positiiviset ja negatiiviset kulmat.
Anna meillä on OA: n ja OI-säteiden muodostama kulma (kuva.18). Liikkuva säde, joka pyörii OA O: n alkuasennosta (OA), voi ottaa lopullisen asennon kahdella eri pyörimisnopeudella. Nämä ohjeet on esitetty kuvassa 1.8 vastaavilla nuolilla.

Kuva.7

Aivan kuten numeerisella akselilla, yksi kahdesta suunnasta pidetään positiivisena, ja toinen on negatiivinen, erotettava kaksi erillistä pyörimisnopeutta erotetaan. Sovittiin olevan positiivinen pyörimissuunta, joka suunta, joka on vastapäivään vastapäivään. Kierto-suunta on samansuuntainen myötäpäivään, pidetään negatiivisena.
Näiden määritelmien mukaisesti kulmat jakautuvat myös positiivisiin ja negatiivisiin.
Positiivista kulmaa kutsutaan kulmaan, joka on muodostettu liikuteltavan säteen pyörimisnä lähtöpisteen ympärille positiivisessa suunnassa.

Kuvassa 1.9 on joitakin positiivisia kulmia. (Siirrettävän säteen pyörimissuunta on esitetty nuolien piirustuksissa.)
Negatiivista kulmaa kutsutaan kulmaan, joka on muodostettu liikkuvan säteen pyörimiseksi lähtöpisteen ympärille negatiivisessa suunnassa.
Kuva 1.10 esittää joitain negatiivisia kulmia. (Siirrettävän säteen pyörimissuunta on esitetty nuolien piirustuksissa.)

Mutta kaksi samankaltaisia \u200b\u200bsäteitä voivat myös muodostaa ja kulmat + 360 ° P ja -360 ° C (n \u003d 0,1,2,3, ...). Merkitsee käyttämällä pienintäkään ei-negatiivisen kiertokulman, joka on siirtänyt OA-säteen OA-asemaan. Jos nyt OV: n säde on lisäksi täydellinen kierros pisteen ympäri, saamme toisen arvon kulman, nimittäin: AVO \u003d B + 360 °.
Ympyrän kaarien kulmien mittaus. Kaaren ja kulmien mittayksiköt
Joissakin tapauksissa osoittautuu käteväksi mitata kulmat ympyrän kaaren avulla. Mahdollisuus tällaiseen mittaukseen pohjalle tunnetulle tasolle, että keskuskulmat ja vastaavat kaaret ovat suorassa suhteellisessa suhteessa niistä ovat yhdessä ympyrässä.
Anna tämän ympyrän kaaren, joka hyväksyttiin kaaren mittayksikköä kohden. Tämän kaaren vastaava keskeinen kulma ottaa kulmien mittayksikön. Tällä tilalla kaikki ympärysmittarit ja vastaava keskuskulma vastaavat tätä kaaria, sisältävät saman määrän mittayksiköitä. Siksi ympyrän kaaren mittausmittaus on mahdollista määrittää näiden kaaren vastaavien keskuskulmien suuruus.
Harkitse kahta yleisimpiä järjestelmiä kaaristen ja kulmien mittaamiseksi.
Asteen mittauskulmat
Kulmien asteikäyttämisen aikana kulmien pääyksikkönä kulmien mittayksikkönä (vertailukulma, jolla verrataan erilaisia \u200b\u200bkulmia) kulma otetaan yhteen asteeseen (nimetty 1?). Yhden asteen kulma on kulma, joka on yhtä suuri kuin 1/180 laajennettu kulma. Kulma, joka vastaa 1/60 kulmaa 1 °: n kulmasta, on yhden minuutin kulma (nimetty 1 "). Kulma, joka vastaa 1/60 osaa kulmasta minuutissa, on kulma sekunnissa (nimetty 1").
Radian kulman mittausmittaus
Yhdessä geometrian ja trigonometrian kulmien asteen mittausmittausta käytetään myös muuta mittausmittausta, jota kutsutaan radialiksi. Harkitse RADIUS R: n ympyrä O. Meillä on kaksi sädettä A: sta ja OB: stä niin, että AV-kaaren pituus on yhtä suuri kuin ympyrän säde (kuva 1.12). Samanaikaisesti saadun AOS: n keskeinen kulma on yhden radianin kulma. Radiculaarisen mittausmittausmittauksen mittayksikköä käytetään 1 radian kulmassa. Kun kulmat ovat radiac, yksityiskohtainen kulma on yhtä suuri kuin R-radialaiset.

Kulmien mittausyksikkö ja radian yksiköt liittyvät tasa-arvoihin:
1 Radian \u003d 180? / P57 ° 17 "45"; 1? \u003d P / 180 radian0.017453radian;
1 "\u003d p / 180 * 60 Radian0.000291 Radian;
1 "" \u003d R / 180 * 60 * 60 Radian0.000005 Radian.
Kulman tutkinnon (tai radian) mittausta kutsutaan myös kulmaan. AOS: n kulma-arvo on joskus merkitty /
Kuljetusluokitus
Kulma, joka on 90 ° tai P / 2 radikulaarisessa mittauksessa, kutsutaan suoriksi kulmaksi; Se on usein merkitty kirjain d. Alle 90 °: n kulma kutsutaan teräväksi; Kulma on suurempi kuin 90 °, mutta pienempi 180 ° kutsutaan typeriksi.
Kaksi kulmaa, joilla on yksi yhteinen puoli ja 180 ° komponentteja kutsutaan vierekkäisiin kulmiin. Kaksi kulmaa, joilla on yksi yhteinen puoli ja 90 asteen komponentteja kutsutaan ylimääräisiksi kulmiksi.
Kuljettavat kulmat trigonometriseen ympyrään.
Huomio!
Tämä aihe on ylimääräisiä
Materiaalit erikoisosassa 555.
Niille, jotka ovat voimakkaasti "ei kovin ..."
Ja niille, jotka ovat "hyvin ...")
Hän on melkein kuin edellisessä oppitunnissa. On akseleita, ympyrä, kulma, kaikki sijoitus chinar. Lisätty neljäsosa (suuren neliön kulmat) - ensimmäisestä neljäsosaan. Ja sitten mitä jos joku ei tiedä? Kuten näet, neljäsosa (niitä kutsutaan myös kauniiksi "kvadrants") numeroiksi myötäpäivään. Lisätty kulma-arvot akseleilla. Kaikki on selkeä, ei ongelmia.
Ja vihreä nuoli on lisätty. Plus. Mitä se tarkoittaa? Haluan muistuttaa, että nurkan paikallaan oleva puoli aina Se on naulattu positiiviseen puoliakseliin Oh. Joten, jos kääntämme kulman liikkuvan puolen nuolella plus. Nousevat Quartanumerot, kulmaa pidetään positiivisena. Esimerkiksi kuvassa on positiivinen kulma + 60 °.
Jos pidämme kulmista vastakkaiseen suuntaan myötäpäivään nuolta pitkin, kulmaa pidetään negatiivisena. Hiiri kuvassa (tai napauta Tablet-kuvia), katso sininen nuoli miinus. Tämä on kulmien negatiivisen viitteen suunta. Esimerkiksi negatiivinen kulma on esitetty (60 °). Ja näet, miten diquses on muuttunut akseleilla ... siirsin myös negatiivisiin kulmiin. Numerointi Quadrants ei muutu.
Täällä, yleensä ensimmäiset väärinkäsitykset alkavat. Kuinka niin!? Ja jos ympyrän negatiivinen kulma on sama kuin positiivinen!? Ja yleensä osoittautuu, että liikkuvan puolen (tai numeerisen ympyrän) samaa sijaintia voidaan kutsua negatiiviseksi kulmaksi ja positiiviseksi!?
Joo. Tarkalleen. Sanotaan positiivinen kulma 90 astetta, joka sijaitsee ympyrässä täysin sama Tilanne on negatiivinen kulma miinus 270 astetta. Positiivinen kulma, esimerkiksi + 110 ° astetta täysin sama asento negatiivisena kulmana -250 °.
Ei ongelmaa. Edellä oikein.) Kulman positiivisen tai negatiivisen laskennan valinta riippuu tehtävän kunnosta. Jos mitään ei sanota avaa teksti noin kulmamerkki, (tyyppi "määrittää pienimmät positiivinen Kulma "jne.), Työskentelemme mukavilla arvoilla.
Paitsi (ja miten ilman niitä?!) Ovat trigonometriset epätasa-arvot, mutta siellä hallitsemme tämän sirun.
Ja nyt kysymys sinulle. Kuinka tunnistan, että 110 ° kulman sijainti on samansuuntainen kulman asentoa -250 °?
Lempinimi, että tämä johtuu koko kierroksesta. 360 ° ... ei ole selvää? Piirrä sitten ympyrä. Piirrämme paperilla. Me merkitse kulma noin 110 °. JA harkitakuinka paljon se on täysi liikevaihto. Se pysyy vain 250 ° ...
Sai kiinni? Ja nyt - Huomio! Jos kulmat ovat 110 ° ja -250 ° miehittävät ympyrässä sama
Asema, mitä? Kyllä, että kulmat ovat 110 ° ja -250 ° täysin identtinen
Sinus, Kosinus, tangentti ja cotangent!
Nuo. SIN110 ° \u003d SIN (-250 °), CTG110 ° \u003d CTG (-250 °) ja niin edelleen. Tämä on jo todella tärkeää! Ja itsessään - on paljon tehtäviä, joissa on tarpeen yksinkertaistaa lausekkeita ja tukikohta myöhemmässä kehityksessä trigonometrian tuomisen ja muun viisauden.
Tyhjennä kotelo, 110 ° ja -250 ° otin Namanumin, pelkästään. Kaikki nämä tasa-arvoisuudet toimivat mihin tahansa kulmiin, jotka käyttävät yhtä kantaa ympyrässä. 60 ° ja -300 °, -75 ° ja 285 ° ja niin edelleen. Huomaa välittömästi, että nämä pariskunnat - eri. Ja tässä on trigonometriset toiminnot - sama.
Mielestäni tällaiset negatiiviset kulmat ymmärrät. Se on melko yksinkertainen. Vastapäivään edistymisestä - positiivinen lähtölaskenta. Kurssilla - negatiivinen. Lue kulma positiivinen tai negatiivinen riippuu meistä. Meidän halusta. No, ja Tehtävästä, tietenkin ... Toivottavasti ymmärrät ja miten liikkua trigonometriisilla toiminnoilla negatiivisista kulmista positiiviseksi ja takaisin. Piirrä ympyrä, likimääräinen kulma, mutta katso, kuinka paljon puuttuu täysi liikevaihto, ts. jopa 360 °.
Kulmat ovat suurempia kuin 360 °.
Kulmat, jotka ovat yli 360 °. Onko olemassa sellaisia? Tietenkin on tietenkin. Kuinka piirtää ne ympyrään? Kyllä, ei ongelma! Oletetaan, että meidän on ymmärrettävä, mikä neljännes saa 1000 °: n kulman? Helposti! Teemme yhden täydellisen käännöksen myötäpäivään (kulma annettiin positiiviseksi!). Siirretty 360 °. No, ja tuuli! Toinen kierros - jo se osoittautui 720 °. Kuinka paljon on jäljellä? 280 °. Täydellinen kierros ei riitä ... mutta kulma on suurempi kuin 270 ° - ja tämä on raja kolmannen ja neljännen vuosineljänneksen välillä. Se oli kulmassa 1000 °: ssa neljännen vuosineljänneksen. Kaikki.
Kuten näette, se on melko yksinkertaista. Jälleen kerran muistutan, että kulma on 1000 ° ja 280 ° kulma, jonka pääsimme hylkäämällä "tarpeettomat" täydelliset kierrosta - se on tiukasti, eri Kulmat. Mutta trigonometriset toiminnot näistä kulmista täysin identtinen! Nuo. SIN1000 ° \u003d SIN280 °, COS1000 ° \u003d COS280 ° jne. Jos olisin sinus, en huomaa ero näiden kahden kulman välillä ...
Miksi tarvitset kaiken tämän? Miksi meidän on käännettävä kulmat yhdestä toiseen? Kyllä, kaikki on sama.) Ilmoitusten yksinkertaistamiseksi. Ilmaisujen yksinkertaistaminen, itse asiassa koulun matematiikan päätehtävä. No, tiellä, pää on koulutusta.)
No, käytäntö?)
Vastaa kysymyksiin. Ensimmäinen yksinkertainen.
1. Mikä neljännes kulma -325 ° Fall?
2. Mikä neljännes on 3000 °: n kulma?
3. Mikä neljännes kulma -3000 ° putoaa?
On ongelma? Tai epävarmuus? Siirrymme kohtaan 555, käytännön työtä trigonometrisen ympyrän kanssa. Siellä, ensimmäisessä oppitunnissa tämä erittäin "käytännön työ ..." Kaikki on yksityiskohtainen ... sellainen Turvallisuusongelmat ei!
4. Mitä merkkiä SIN555 ° on?
5. Mikä merkki on TG555 °?
Määritelty? Erinomainen! Epäillä? On tarpeen 555 §: llä ... muuten, he oppivat tekemään tangentia ja cotagent trigonometriseen ympyrään. Erittäin hyödyllinen asia.
Ja nyt kysymyksiä juuressa.
6. Todista ilmentymä SIN777 ° pienimmän positiivisen kulman sinuson.
7. Luo ekspressio COS777 ° suurimman negatiivisen kulman kosiniin.
8. Anna COS-lauseke (-777 °) pienimmän positiivisen kulman sekiiniin.
9. Vahvistaa ilmaisun SIN777 ° sinus korkeimmalla negatiivisella kulmalla.
Mitä kysymyksiä 6-9 hämmentynyt? Tutustu tenttiin eikä tällainen sanamuoto tavata ... niin, käänny. Vain sinulle!
Sanat "tuo lauseen ..." tarkoittaa ilmaisua niin, että sen arvo ei muuttunut Ja ulkonäkö on muuttunut tehtävän mukaisesti. Joten, tehtävässä 6 ja 9 meidän on saatava sinus, jonka kuluessa se maksaa mykistä positiivinen kulma. Kaikki muu - sillä ei ole väliä.
Vastaukset annetaan järjestyksessä (sääntöjen rikkomisesta). Ja mitä tehdä, merkki on vain kaksi, ja neljännes on vain neljä ... et toimi vaihtoehdoissa.
6. SIN57 °.
7. COS (-57 °).
8. COS57 °.
9. -Sin (-57 °)
Oletan, että vastaukset kysymyksiin 6 -9 joku sekava. Erikoinen -sin (-57 °)Onko totta?) Todellinen?) Todellakin, vertailukulmien perussäännöissä on paikka virheitä varten " Osa 555. On 4-9 tehtäviä puretaan. Hyvin purettu, kaikki vedenalaiset kivet. Ja he ovat täällä.)
Seuraavassa oppitunnissa käsitellään salaperäisiä radiaaneja ja numeroa "Pi". Opimme helposti ja oikein kääntämään tutkintoja radiaaniksi ja takaisin. Ja yllätys huomaat, että tämä perustietoa sivustolla jo tarttuu Voit ratkaista joitakin ei-standardi Trigonometria Tehtäviä!
Jos pidät tästä sivustosta ...
Muuten minulla on toinen pari mielenkiintoista sivustoa sinulle.)
Sitä voidaan käyttää ratkaisemaan esimerkkejä ja selvitä tasosi. Testaus instant check. Opi - kiinnostuneena!)
Voit tutustua ominaisuuksiin ja johdannaisiin.
Trigonometriassa tärkeä käsite on pyörimisaulus. Allamme jatkuvasti ajatella kiertoa ja anna kaikki samanaikaiset käsitteet. Aloitamme vuoron yleisestä esityksestä, sanotaan koko vuorosta. Seuraavaksi siirrymme kiertokulman käsitteeseen ja käsittelemme sen pääominaisuuksia, kuten pyörimisen suunnan ja suuruuden. Lopuksi annamme määritelmän kuvan muodostaen pisteen ympärillä. Kaiken tekstin teorian toimitetaan selittävät esimerkit ja graafiset kuvat.
Navigointi sivu.
Mitä kutsutaan kääntämällä pisteen ympäri?
Välittömästi huomaamme, että ilmaisulla "kääntyy pisteen ympärille" käytämme myös lause "kääntyä pisteen ympärille" ja "kääntyy suhteessa pisteeseen", mikä tarkoittaa samaa.
Esittelemme pisteen pyörimisen käsite pisteen ympärillä.
Ensin annamme pyörimiskeskuksen määritelmän.
Määritelmä.
Kohta suhteessa, joihin kääntyy kääntöä kääntökeskus.
Nyt sanotaan, mitä saadaan pisteen pyörimisen seurauksena.
Joidenkin pisteen pyörimisen seurauksena on suhteessa kääntökeskukseen O, piste A 1 saadaan (joka tietyn määrän tapauksessa voi olla samanaikainen a) ja kohta A 1 piilee ympyrässä Keskus OA: n sädepisteessä. Toisin sanoen, kun käännytään suhteessa pisteeseen O-pisteeseen prosessit pisteeseen A 1, joka makaa ympyrässä keskellä OA: n sädepisteessä.
Uskotaan, että kohta O, kun se kääntyi itsensä ympärille. Tämä on seurauksena pyörimiskeskuksen ympäri, kohta O menee itselleen.
On myös syytä huomata, että pisteen A ympärillä O olevan pisteen o on katsottava siirtyväksi pisteen A ympärillä olevan ympyrän liikkeen seurauksena keskellä OA: n sädepisteessä.
Selkeyden vuoksi esitämme esimerkin pisteen pyörimisestä ja sen ympärillä, alla olevissa kuvissa, siirrä piste A pisteeseen A 1, näytämme nuolen avulla.
Täysi kierros
Voit tehdä tällaisen pyörimisen pisteen A suhteessa kierrosta O: n keskelle, mikä osoittaa, että kaikki ympyrän kohdat kulkevat, osoittautuu samaan paikkaan. Samalla he sanovat, että piste, joka on suoritettu pisteen O.
Annamme graafinen kuva koko liikevaihdosta.

Jos et pysähdy yhdellä kierroksella, vaan jatkaa pisteen liikkumista ympärysmitta, voit suorittaa kaksi, kolme ja niin täydellisiä kierroksia. Oikein alapuolella olevassa piirustuksessa osoittaa, kuinka kaksi täydellistä kierrosta voidaan tuottaa, ja vasen on kolme kierrosta.

Kiertokulman käsite
Ensimmäisessä kohdassa esitetystä pisteestä pyörimispiste on selvää, että pisteen ja sen ympärillä on ääretön joukko pyörimispisteitä. Itse asiassa minkä tahansa kehän pistettä keskustaan \u200b\u200bOA: n sädepisteessä voidaan pitää pisteenä A 1, joka on saatu pisteen a pyörimisen seurauksena. Siksi erottaa toinen käännös toisesta, käyttöön kiertokulman käsite.
Yksi pyörimiskulman ominaisuuksista on kääntää. Kiertämissuuntaan arvioi, miten pisteen kierto suoritetaan - myötäpäivään tai vastapäivään.
Toinen ominaisuus pyörimiskulma on sen arvo. Kiertokulmat mitataan samoissa yksiköissä kuin: yleisimmät tutkinnot ja radialaiset. On syytä huomata, että pyörimiskulma voidaan ilmaista asteina millä tahansa reaaliluvulla äärettömän miinusin välein äärettömyyteen, toisin kuin geometrian kulma, jonka arvo on positiivinen asteina eikä se ole ylittää 180.
Kreikan aakkosen pieniä kirjaimia käytetään yleisesti: jne. Viitata lukuisiin kääntöjen kulmiin, yksi kirjain, jossa on pienemmät indeksit, käytetään usein, ![]() .
.
Puhutaan nyt pyörimiskulman ominaisuuksista enemmän ja järjestyksessä.
Kääntää
Anna ympyrän keskellä pisteessä O merkitty piste A ja 1. Kohdassa A 1 voit saada pisteestä A kääntämällä keskusta O joko myötäpäivään tai - vastapäivään. Nämä käännökset pidetään loogisesti erilaisia.
I havainnollistamme kääntyy positiiviseen ja negatiiviseen suuntaan. Alla olevassa piirustuksessa käänne näkyy positiivisessa suunnassa ja oikealla - negatiivisella.

Pyörimisen kulman suuruus, mielivaltainen kulma
Muun muunnon kuin pyörimiskulman kulma määräytyy täysin sen arvosta, toisaalta vuorotellen vuoron kulman arvoa voidaan arvioida siitä, miten tämä kierros suoritettiin.
Kuten edellä on jo mainittu, pyörimiskulman suuruus asteittain ilmaistaan \u200b\u200bnumerolla -∞ - + ∞. Tällöin plus-merkki vastaa kääntyä myötäpäivään ja miinusmerkki pyörii vastapäivään.
Nyt on vielä muodostettava kirjeenvaihto kiertokulman arvon ja se, että se vastaa.
Aloitetaan pyörimiskulma, joka on yhtä suuri kuin nolla aste. Tämä kulma kääntyy pisteen ja itsessään. Toisin sanoen, kun kääntämällä 0 astetta pisteen O kohta pysyy paikallaan.
Siirry pisteen pyörimiseen ja pisteeseen O, jossa kierto tapahtuu puolen liikevaihdosta. Oletamme, että kohta a siirtyy 1: een. Tällöin AOA 1: n absoluuttinen kulma ei ylitä 180. Jos pyöriminen tapahtui positiivisessa suunnassa, pyörimisen kulman suuruus pidetään yhtä suurina kuin AOA 1: n kulma ja jos pyöriminen esiintyy negatiivisessa suunnassa, sen arvoa pidetään yhtä suurina kuin AOA: n kulma 1 miinusmerkki. Esimerkiksi esitämme piirustuksen, joka esittää 30, 180 ja -150 asteen pyörimiskulmia.

Kiertokulmat ovat suuria 180 astetta ja pienempi -180 astetta määritetään seuraavien riittävän ilmeisen perusteella peräkkäisten käännösten ominaisuudet: Useat pisteen sarjan A ympärille keskiosaa o ovat yhtä kierrosta, jonka arvo on yhtä suuri kuin näiden kierrosten arvo.
Anna meille esimerkki, joka kuvaa tätä ominaisuutta. Kierrämme pisteen A suhteessa O 45 asteeseen ja käännä sitten tämä kohta 60 astetta, minkä jälkeen käännymme tämän pisteen -35 asteen. Merkitsee välipisteitä näissä käännöksinä 1, A 2 ja 3. Samassa pisteessä ja 3 voisimme saada suorittamalla yhden pisteen A 45 + 60 + 35) \u003d 70 astetta.

Joten pyörimiskulmat, suuret 180 astetta, edustamme muutaman peräkkäisen kierroksen kulmissa, joiden arvot antavat arvon alkukulman pyörimisen kulman arvon. Esimerkiksi 279 asteen kiertokulma vastaa 180 ja 99 astetta tai 90, 90, 90 ja 9 astetta tai 180, 180 ja -81 astetta tai 279 peräkkäistä kierrosta 1 astetta.
Kiertokulmat määritellään samalla tavalla, pienempiä -180 astetta. Esimerkiksi pyörimiskulma -520 astetta voidaan tulkita johdonmukaisiksi kierroksiksi -180, -180 ja -160 astetta.
Tiivistää. Olemme määrittäneet pyörimisen kulman, jonka suuruus on asteina jonkin verran voimassa olevasta numerosta aukosta -∞ - + ∞. Trigonometriassa työskentelemme kääntökulmilla, vaikka sana "kääntyy" usein lasketaan, ja he sanovat yksinkertaisesti "kulman". Näin ollen Trigonometryssä toimimme kulmakulmilla, jolloin ymmärrämme käännöksen kulmat.
Tämän kohdan perusteella huomaamme, että positiivisen suunnan kokonaisliikevaihto vastaa 360 astetta (tai 2 π radiaania) ja negatiivisena - pyörimiskulma -360 asteessa (tai -2) · Π on iloinen). Samalla se on kätevä suuria kulmia, jotka edustavat tiettyyn määrään täydellisiä kierroksia ja toinen kierros suuruuskulma -180 - 180 astetta. Ota esimerkiksi 1,340 asteen pyörimiskulma. Se on helppo edustaa 1 340 360 · 4 + (- 100). Toisin sanoen ensimmäinen kiertokulma vastaa 4 täyttä kierrosta positiivisessa suunnassa ja seuraavaksi käännetään -100 astetta. Toinen esimerkki: pyörimiskulma -745 astetta voidaan tulkita kaksi kierrosta myötäpäivään nuolta ja sen jälkeen -25 astetta, koska -745 \u003d (- 360) · 2 + (- 25).
Kierrä muotoa pisteen ympärille kulmassa
Kohdon kierto käsite laajenee helposti kierrä mitään muotoa pisteen ympärille kulmassa (Tämä koskee tällaista vuoroa kuin kohta suhteessa, johon kääntö suoritetaan ja kuvio, joka kääntyy, valehdella samassa tasossa).
Kuvan vaihteessa ymmärrämme kaikkien kuvion pisteiden pyörimisen tietyn kohdan ympärillä tietyllä kulmalla.
Esimerkkinä annamme esimerkin seuraavista toiminnoista: Suorita leikatun AB: n kierto kulmaan suhteessa pisteeseen O, tämä segmentti kääntyy muuttumalla segmenttiin 1 b 1.

Bibliografia.
- Algebra: Opinnot. 9 cl. ympäristö Shk. / U. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorov; Ed. S. A. Telikovsky. - M.: Koulutus, 1990.- 272 K.: Il.- ISBN 5-09-002727-7
- Bashmakov M. I. Algebra ja aloitusanalyysi: tutkimukset. 10-11 cl. ympäristö Shk. - 3. toimita. - M.: Enlightenment, 1993. - 351 C.: IL. - ISBN 5-09-004617-4.
- Algebra Ja aloitusanalyysi: tutkimukset. 10-11 cl. Yleissivistävä koulutus. Toimielimet / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn jne.; Ed. A. N. KOLMOGOROVA.- 14. ED. - M.: Enlightenment, 2004.- 384 K.: Il.- ISBN 5-09-013651-3.
- Gusev V. A., Mordovich A. G. Matematiikka (hyöty hakijoille teknisissä kouluissa): tutkimukset. hyöty. - m.; Korkeampi. Shk., 1984.-351 s., IL.